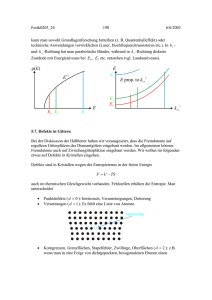
ω ωω + = LT ωπ /2

Mag0304_4.DOC
22
11/12/2003
Gesamtdrehimpuls J = 0 ist: Bi, Ar, Cu, kovalente Halbleiter, Ionenkristalle. Da
χ dia << 1 ist, wirkt am Ort der Atome das angelegte Feld B: B int = B ext .
In einem freien Atom heben sich Zentrifugalkraft und Coulombkraft auf:
m eω 02 r =
Ze 2
.
4πε 0 r 2
Beim Anlegen eines Magnetfelds ändert sich die Frequenz (siehe schöne Herleitung in
Jäger und Perthel)
m eω 2 r =
Ze 2
Ze 2
+
e
(
v
×
B
)
=
+ eω rB .
4πε 0 r 2
4πε 0 r 2
Für die neue Frequenz erhält man
2
 eB 
eB
ω2
 = ω L + ω 0 1 + L2 ,
ω=
+ ω0 1 + 
2me
ω0
 2me ω0 
eB
definieren kann. In
2m e
Laborexperimenten ist normalerweise eB sehr klein (ω L << ω 0 ). Damit erhält man
wobei man auf natürliche Weise die Larmorfrequenz ω L =
ω = ωL +ω0 .
Beachte: Für die Zyklotronresonanz freier Ladungsträger (siehe FestkörperphysikVorlesung) hat man den umgekehrten Grenzfall ω L >> ω 0 , da die Fermigeschwindigkeit
viel kleiner ist als ω 0 r und man erhält: ω c = ω = ω L + ω L = 2ω L . Die Zyklotronfrequenz
ist also “doppelt so gross” wie die Larmorfrequenz.
Die Larmorfrequenz von Z Elektronen entspricht einem Strom, der gegeben ist durch
( T = 2π / ω L )
I = ( −Ze)
ω
1
eB
Ze2 B
= ( −Ze) ⋅ L = (−Ze)
=−
.
T
2π
4πme
4πme
Wir berechnen jetzt die Magnetisierung: Dazu muss man zuerst das magnetische Moment
berechnen
Ze 2 B
Ze 2 B 2
µ dia = IA = −
π ρ2 = −
ρ .
4π me
4me
Mag0304_4.DOC
23
11/12/2003
Zur Illustration nehmen wir eine kugelförmige Ladungsverteilung an. Damit erhält man
für das mittlere Abstandsquadrat
ρ 2 = x2 + y 2 =
2 2
r .
3
Für die Magnetisierung folgt (n: Anzahl Atome pro Volumeneinheit)
M = nµ dia = −
ne 2 B
Z r2 .
6me
Damit erhält man für die diamagnetische Suszeptibilität das klassische Langevin
Ergebnis
M µ0 M
µ ne 2
χ dia =
=
=− 0
Z r2 .
H
B
6me
Cu
χ dia ist sehr klein, Beispiel Kupfer: χ dia
= −1.1 ⋅10 −6 und rechtfertigt die Annahme,
dass B int ≅ B ext ist. Beachte, das Z sollte als eine Art effektives Z interpretiert werden.
Viele Materialien werden gut mit dem Modell von Langevin beschrieben, das im
wesentlichen auf eine Berechnung des mittleren Abstandquadrats der Elektronen
hinausläuft. Wir werden sehen, dass auch magnetische Materialien einen
diamagnetischen Beitrag liefern, der meist sehr klein ist und vernachlässigt werden kann.
Die diamagnetische Suszeptibilität hängt innerhalb der getroffenen Annahmen nicht von
der Temperatur ab.
1.3.6. Diamagnetismus: Quantenmechanische Behandlung
Wir wollen jetzt den Diamagnetismus mit Hilfe der Quantenmechanik herleiten. Wir
betrachten dazu den Hamiltonoperator eines Atoms
Z
 p2

H 0 = ∑  i + Vi (r )  ,
i =1  2m e

der sich aus der kinetischen Energie und der potentiellen Energie der Z Elektronen
zusammensetzt. Die Eigenwerte und Wellenfunktionen von H0 seien bekannt. Nun legen
wir ein Magnetfeld B an und wählen die Eichung
A(r ) =
1
(B × r)
2
Mag0304_4.DOC
24
11/12/2003
für das Vektorpotential A. Aus der Quantenmechanik ist bekannt, dass man im
Hamiltonoperator den Impuls p durch den kanonischen Impuls p − qA ersetzten muss.
Man erhält ( q = −e , µ B = − eh /( 2m e ) )
Z
Z
 (p + eA (ri )) 2

ep i ⋅ A(ri ) e 2 A( ri ) 2
H = ∑  i
+ Vi (r )  + gµ B B ⋅ S = H 0 + ∑
+
+ gµ B B ⋅ S i
2me
me
2m e
i =1 
i =1

Z
H = H0 + ∑
i =1
ep i ⋅ (B × ri ) e 2 (B × ri ) 2
+
+ gµ B B ⋅ S =
2me
8me
e2
8 me
H = H 0 + µ B ( L + g S)B +
Z
∑ (B × r )
2
i
.
i =1
Hier haben wir L = ∑ L i und S = ∑ S i gesetzt. Der mittlere Term beschreibt den
paramagnetischen Anteil und der letzte Term den diamagnetischen Anteil. Beachte, dass
im obigen Model die Spin-Bahn Kopplung ∝ L ⋅ S in H 0 berücksichtigt ist.
Zur Berechnung der freien Energie brauchen wir einen Ausdruck für die
Energieänderung des Grundzustands in einem Magnetfeld. Für B = (0,0, B z ) erhalten wir
in Störungstheorie 1. Ordnung für den diamagnetischen Anteil
∆E =
e2B 2
8me
Z
∑
0 | xi2 + y i2 | 0 =
i =1
e2B 2
8m e
Z
2
∑3 0|r
i
2
|0 .
i =1
Der letzte Schritt gilt nur für gefüllte Elektronenschalen (L = 0, S = 0, J = 0), weil nur
dann die Ladungsverteilung kugelsymmetrisch ist. Aus der Thermodynamik
( dF = − SdT − pdV − MdB ) folgt für n Atome pro Volumeneinheit
M =−
∂F
∂E
e 2B Z 2
= −n
= −n
∑ ri .
∂B
∂B
6me i=1
Damit erhält man für die diamagnetische Suszeptibilität in Störungstheorie 1. Ordnung
einen fast identischen Ausdruck wie in der klassischen Näherung:
χ dia
M
µ0 M
µ 0 ne2
=−
≅−
=−
H
B
6me
Z
∑
ri 2 .
i =1
In erster Näherung ist χ dia wiederum unabhängig von T, da angeregte Zustände meistens
nur schwach populiert sind.
Mag0304_4.DOC
25
11/12/2003
Im Prinzip sind nur die Elektronen in den äusseren Schalen wichtig, da der Term ri 2 für
die inneren Schalen klein ist (stimmt das?) und man kann Z durch Z eff ersetzen und
erhält
χ dia ≅ −
µ 0 ne 2
Z eff r 2 ,
6m e
wobei r der Radius der äusseren Schale ist. In ionischen Kristallen wie NaF, NaCl etc.
beobachtet man tatsächlich dieses Verhalten (siehe Figur 2.2 in Blundell). Für Moleküle
mit delokalisierten π-Elektronen wie Graphit ist χ dia anisotrop: Gross für B senkrecht
zur Ebene und klein für B in der Ebene. Beachte: Falls Elektronenschalen nicht
vollständig gefüllt sind, ergeben sich positive Werte für χ (à Paramagnetismus), die
viel grösser sind als χ dia (siehe Ashcroft Mermin, p. 648).
Grössenordnung der Suszeptibilität: Für r = 1 Å erhält man (siehe Jäger und Perthel p.
15) χ dia = −35 .4 ⋅10 −12 m 3 Mol −1 . Für den Beitrag von Leitungselektronen siehe JP p. 16.
1.3.7. Paramagnetismus
Paramagnetismus tritt in Materialien mit einer ungeraden Zahl von Elektronen auf.
Sauerstoff ist aber ein Beispiel eines paramagnetischen Materials mit einer geraden
Anzahl von Elektronen. Diese Materialien haben bereits in Nullfeld ein magnetisches
Moment, im Gegensatz zu diamagnetischen Materialien, in denen das Moment durch das
äussere Feld induziert wird.
Liegt kein Feld an, zeigen die Momente in willkürliche Richtungen. Bei sehr hohen
Feldern werden alle Momente ausgerichtet und der Körper ist vollständig magnetisiert.
Für eine halbklassische Betrachtungsweise verweisen wir auf die Literatur (Blundell p.
23) und die Vorlesung Festkörperphysik. Das klassische Ergebnis lautet:
µz
µ
= coth( y ) −
1
≡ L( y ) .
y
L( y ) nennt man Langevin-Funktion, y = µB /( k B T ) und µ z bezeichnet das mittlere
Moment entlang B. Im Grenzfall y << 1 erhält man
µz
µ
≅
µB
3k BT
woraus folgt:
χ=n
µ 0µ 2
.
3k BT
Mag0304_4.DOC
26
11/12/2003
Das Ergebnis zeigt, das χ umgekehrt proportional zu T ist (Curie-Gesetz), was man
auch tatsächlich beobachtet. Die Curie-Konstante C = nµ 0 µ 2 /( 3k B ) ist aber nur korrekt
für „klassische“ Spins, d.h. wenn µ >> µ B ist.
Als nächstes betrachten wir jetzt ein quantenmechanisches System mit S = 12 . Das
magnetische Moment ist gegeben durch
µ = − gµB S .
Legt man ein Magnetfeld an, dann erzeugt man 2 Zeeman-Niveaus deren Energie
gegeben ist durch (wir setzen g = 2.0000)
E = −µ ⋅ B = ± µ B B .
Die Besetzung der zwei möglichen Zustände m1 / 2 = ± 12 ist gegeben durch BoltzmannFaktoren exp( − E / k B T ) . Mit der Abkürzung x ≡ µ B B /( k B T ) erhält man
N −1
ex
= x
+ N 1 e + e−x
mJ
µL
1/2
-µB
-1/2
µB
2
N −1
2
2
2µBB
N1
2
N −1 + N 1
2
2
=
−x
e
.
e + e−x
x
1.0
Besetzung des
unteren Zustands
Besetzung
0.8
0.6
0.4
Besetzung des
oberen Zustands
0.2
0.0
0
1
2
x = µΒB/kB T
3
4
File Magnetismus.opj
Die Magnetisierung der Probe ist gerade proportional zur Differenz der beiden Kurven
und man erhält mit N = N − 1 + N 1
2
2
Mag0304_4.DOC
27
M =
11/12/2003
1
e x − e− x
µ B
(N −1 − N 1 )µ B = n µB x
= nµ B tanh B .
−
x
2
2
V
e +e
kBT
Für x << 1 , d.h. hohe Temperaturen ist tanh x ≅ x und man erhält
M = nµ B
µ B B nµ B2
=
,
kBT
k BT
Für die paramagnetische Suszeptibilität folgt
χ para ( S = 12 ) =
2
2 2
M µ 0 M nµ 0 µ B nµ 0 g µ B S ( S + 1)
≅
=
=
,
H
B
k BT
3k BT
das um einen Faktor 3 vom klassischen Langevin-Resultat abweicht. Für S = 12 ist es
besonders dramatisch, da S ( S + 1) =
3
4
≠ S2 =
1
4
ist!
100
0.20
Suszeptibilität
80
0.16
0.12
χpara = C/T
40
-1
χpara = T/C
20
0
1/χpara
χ para
60
0.08
0.04
0
40
80
T (K)
120
0.00
160
File Magnetismus.opj
Berechnung für allgemeine J:
Für beliebige J hat man 2 J + 1 Niveaus und man erhält für die potentielle Energie E J z
EJz eines Moments mit der z-Komponente des Drehimpulses J
EJ z = gµ B J z Bz .
Der g-Faktor ist gegeben durch die Landé-Gleichung:
Mag0304_4.DOC
28
11/12/2003
J ( J + 1) + S ( S + 1) − L ( L + 1)
.
2 J ( J + 1)
g = 1+
Unter der Annahme, dass die Energie für die angeregten J-Multipletts viel grösser ist als
E J z = gµ B JB z , dann erhält man für die Magnetisierung
J
M =n
∑ gµ
J z =− J
B
J ze
J
∑
e
− E J z / k BT
− E J z / k BT
= ngµ B
∑ ( J / J )e
J
∑e
aJ z / J
z
aJ z / J
,
J z =− J
wobei a = gµ 0µ B JH /( k BT ) . Man sieht, dass der Zähler gerade der Ableitung des
Nenners entspricht und man erhält
M = ngµ B J
d  J aJ z / J
ln ∑ e
da  J z =− J

.


Dies ist eine geometrische Reihe mit dem Quotienten e − a / J und es ergibt sich durch
Summation und daraus folgende Differentiation der Ausdruck
 gµ µ JH
 2J + 1
 2J +1 1
 a 
M = ngµ B J 
coth a
coth  = ngµ B JB j  0 B
−
 2J  2J
 2 J 
 2J
 k BT

 .

B J (a ) nennt man die Brillouin-Funktion. Für J = 12 erhält man natürlich wieder das
Resultat B 1 (a ) = tanh( a) .
2
Für den Grenzfall kleiner Magnetfelder ( a << 1 ) kann man BJ (a ) entwickeln und man
erhält
B J ( a) =
J +1
a.
3J
Dann gilt für die Magnetisierung
M = ngµ B J
und die Suszeptibilität
J + 1 gµ 0 µ B JH
H
= ng 2 µ 0 µ B2 J ( J + 1)
3J
k BT
3k B T
Mag0304_4.DOC
χ = ng 2 µ 0 µ B2 J ( J + 1)
29
11/12/2003
H
nµ 0 g 2 µ B2 J ( J + 1) nµ 0 2
C
=
=
µ eff = ,
3k B T
3k B T
3k B T
T
wobei das sogenannte effektive Moment gegeben ist durch
µ eff = gµ B J ( J + 1) .
Man erhält damit wiederum das Curie-Gesetz C ∝ T −1 . Im klassischen Grenzfall J → ∞
wird das Resultat von Langevin reproduziert.
Durch Messen der Temperaturabhängigkeit der paramagnetischen Suszeptibilität kann
man µ eff eines Materials bestimmen, indem man 1/ χ para gegen die Temperatur T
aufträgt. Die Steigung entspricht dann gerade der inversen Curiekonstanten C −1 .
Die folgende Figur nach W. E. Henry, Phys. Rev. 88, 559 (1952) zeigt das magnetische
Moment für die L = 0 Ionen
•
•
•
I: Cr3+ ( S = 3 / 2 )
II: Fe3+ ( S = 5 / 2 )
III: Gd3+ ( S = 7 / 2 ).
0
1
2
3
4
B/T (T/K)
Die Übereinstimmung der Brillouinfunktion mit dem Experiment ist sehr gut.