Lösungsvorschläge Übung 1

Dr. Christian Săcărea
“Babeş–Bolyai” Universität, Cluj-Napoca
Fachbereich Mathematik und Informatik
Sommersemester 2017
Lösungshinweise zur 1. Übung
Algorithmische Graphentheorie für Informatiker
Gruppenübungen:
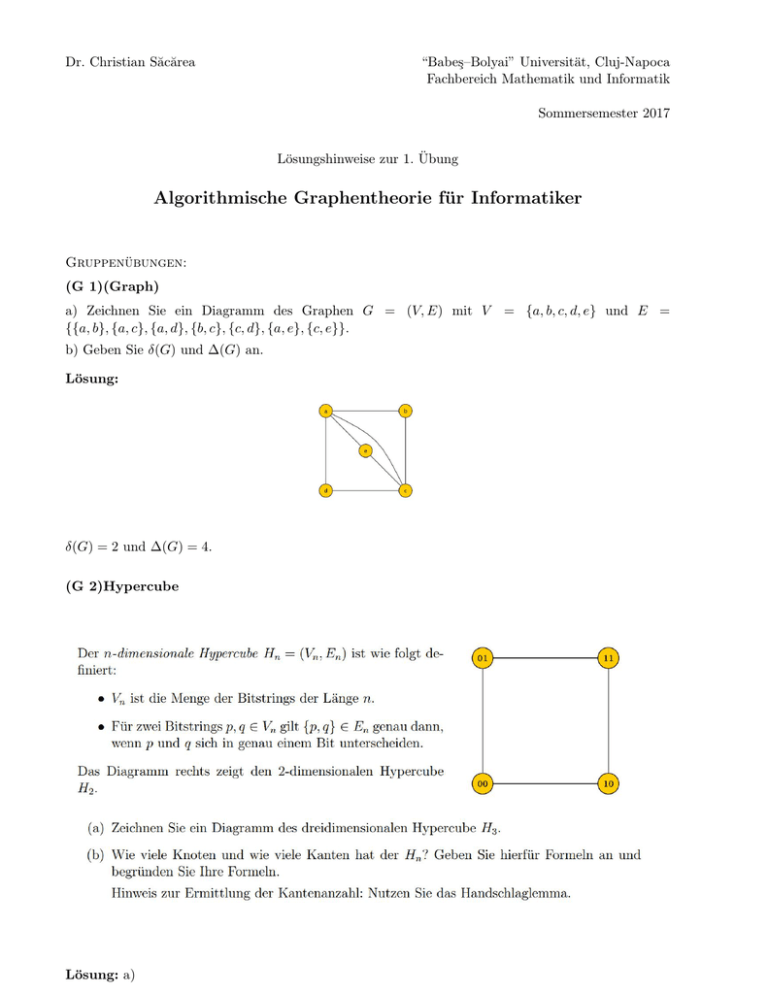
(G 1)(Graph)
a) Zeichnen Sie ein Diagramm des Graphen G = (V, E) mit V
{{a, b}, {a, c}, {a, d}, {b, c}, {c, d}, {a, e}, {c, e}}.
b) Geben Sie δ(G) und ∆(G) an.
Lösung:
δ(G) = 2 und ∆(G) = 4.
(G 2)Hypercube
Lösung: a)
= {a, b, c, d, e} und E =
b)
(G 3)Isomorphie
Welche der folgenden Graphen sind isomorph, und welche nicht?
Lösung: Die ersten zwei ja, der letzte nicht.
(G 4)Gittergraph
Der Gittergraph Qn,m = (Vn,m , En,m ) ist für n, m ≥ 2 definiert durch:
Vn,m = {1, . . . , n} × {1, . . . , m}
En,m = {{(i, j), (i0 , j0 )} | |i − i0 | + |j − j0 | = 1}.
a) Zeichnen Sie den Q2,4 und den Q3,3 .
b) Zeigen Sie mit Hilfe der vollständigen Induktion:
| En,m |= 2nm − n − m.
c) Können Sie die Formel von (b) auch direkt aus dem Handschlaglemma herleiten?
Lösung:
a)
b) Induktionsanfang für n = 2: Ein Q2,m hat
- m Kanten, die die Knoten (1, j) und (2, j) miteinander verbinden,
- m − 1 Kanten, die die Knoten (1, j) und (1, j + 1) miteinander verbinden und
- m − 1 Kanten, die die Knoten (2, j) und (2, j + 1) miteinander verbinden.
Also gilt
| E2,m |= m + (m − 1) + (m − 1) = 3m − 2 = 2 · 2 · m − 2 − m
Also stimmt die Formel für n = 2.
Induktionsschritt n → n + 1: Ein Qn+1,m hat
- Alle Kanten, die auch der Qn,m enthält. Nach I.V. sind dies 2nm − n − m.
- m Kanten, die die Knoten (n, j) und (n + 1, j) miteinander verbinden und
- m − 1 Kanten, die die Knoten (n + 1, j) und (n + 1, j + 1) miteinander verbinden.
Also gilt | En+1,m |= 2nm − n − m + m + (m − 1)
= 2nm + 2m − n − 1 − m
= 2(n + 1)m − (n + 1) − m
c) Ja, dies ist möglich. Im Qn,m haben
- die Knoten {(i, j)|2 ≤ i ≤ n − 1, 2 ≤ j ≤ m − 1} den Grad 4. Dies sind (n − 2)(m − 2) Knoten.
- die Knoten {(1, j) | 2 ≤ j ≤ m} den Grad 3. Dies sind (m − 2) Knoten.
- die Knoten {(n, j) | 2 ≤ j ≤ m} den Grad 3. Dies sind (m − 2) Knoten.
- die Knoten {(i, 1) | 2 ≤ i ≤ n} den Grad 3. Dies sind (n − 2) Knoten.
- die Knoten {(i, m) | 2 ≤ i ≤ n} den Grad 3. Dies sind (n − 2) Knoten.
- die Knoten (1, 1), (1, m), (n, 1), (n, m) den Grad 2. Damit ergibt sich nach dem Handschlaglemma
| En,m |= 12 (4(n − 2)(m − 2) + 6(m − 2) + 6(n − 2) + 8)
= 2(n − 2)(m − 2) + 3(m − 2) + 3(n − 2) + 4
= 2nm − 4m − 4n + 8 + 3m − 6 + 3n − 6 + 4
= 2nm − n − m
Hausübungen:
(H 1)Schubfachprinzip
a) Zeigen Sie: Unter je fünf Punkten in einem gleichseitigen Dreieck der Seitenlänge 1 gibt es stets
zwei, deren Abstand höchstens 1/2 ist.
b) Unter je 17 Punkten in einem gleichseitigen Dreieck der Seitenlänge 1 gibt es stets zwei, deren
Abstand höchstens d ist. Bestimmen Sie einen geeigneten Wert für d und zeigen Sie mit diesem Wert
die Gültigkeit der Aussage.
√
c) Unter je s Punkten in einem Würfel der Seitenlänge 3 gibt es stets zwei, die einen Abstand ≤ 3
haben. Bestimmen Sie einen geeigneten Wert für s.
Lösung:
a) Wir verbinden paarweise die Mittelpunkte der Seiten des gleichseitigen Dreiecks: Dadurch entstehen
vier gleichseitige (Unter-)Dreiecke, deren Seitenlänge stets 1/2 ist. Zwei Punkte in solch einem Dreieck
haben demnach einen Abstand ≤ 1/2. Nach dem Schubfachprinzip mussen von fünf Punkten, die
in dem umschließenden Dreieck mit Seitenlänge 1 liegen, mindestens zwei Punkte in dem selben
Unterdreieck liegen, denn es gibt ja nur vier Unterdreiecke. Diese beiden Punkte haben dann einen
Abstand ≤ 1/2.
b) Wenn man die vier Unterdreicke aus (a) wieder jeweils durch Halbieren der Seitenlänge unterteilt,
entstehen insgesamt 16 gleichseitige Dreiecke mit Seitenlänge d = 1/4. Von 17 Punkten mussen also
mindestens zwei im selben Unterdreieck liegen, die dann einen Abstand ≤ 1/4 haben.
c) Analog zu den Aufgaben (a) und (b), nur dass hier entlang der drei Würfelachsen unterteilt wird.
Jede Achse wird in 3 Teile der Länge
1 unterteilt.√ Dadurch entstehen 33 = 27 Unterwürfel, deren
√
2
Raumdiagonale jeweils die Länge 1 + 12 + 12 = 3 hat. Also s = 28.
(H 2)Schubfachprinzip
P
n − 2. Zeigen Sie, dass es dann zwei
Gegeben seien n natürliche Zahlen a1 , . . . , an mit nk=1 ak ≤ 2P
P
nichtleere Indexmengen I1 , I2 ⊆ {1, . . . , n} mit I1 ∩ I2 = ∅ und i∈I1 ai = i∈I2 ai gibt.