¨Ubungen zur Physik 2 – Lösungen zu Blatt 8

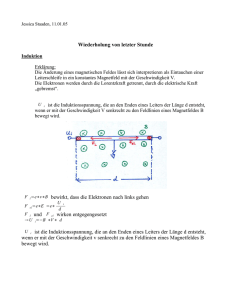
Übungen zur Physik 2 – Lösungen zu Blatt 8
(Dated: April 20, 2010)
I.
LR-KREIS
1. Der Gesamtwiderstand der Schaltung beträgt Rtot = R1 . Da R2 mit einem 0 Ω-Widerstand parallel geschaltet
ist fliesst der gesamte Strom durch die Spule:
I1 = U0 /R1
und
I2 = 0.
(1)
2. Wird der Schalter geöffnet, so fällt aufgrund ihrer Induktivität eine Induktionsspannung an der Spule ab,
welche der Abnahme des Stromes durch die Spule versucht entgegenzuwirken (Lenzsche Regel). Das untere
Ende der Spule (Skizze) liegt also auf positivem Potential, so dass die Induktionsspannung einen Stromfluss im
Uhrzeigersinn durch den Kreis Spule – Widerstand R2 bewirkt.
3. Mit Hilfe der Maschenregel und der Induktionsspannung Uind = −LI˙ erhalten wir die Spannungsbilanz
−LI˙ − R2 I = 0
wobei I den Strom durch die Spule bezeichnet. Diese Differentialgleichung lässt sich durch Separation der
Variablen lösen. Mit der Anfangsbedingung I(t = 0) = I1 ergibt sich das Ergebnis
I(t) = I1 e−t/τ
(2)
wobei die Zeitkonstante τ = L/R2 eingeführt wurde. Den zeitlichen Verlauf der Induktionsspannung erhalten
wir gemäss
Uind (t) = −LI˙ = Umax e−t/τ .
(3)
2
Die maximale Induktionsspannung Umax = I1 R2 = U0 R
R1 wird unmittelbar nach dem Öffnen des Schalters
erreicht.
4. Im Grenzfall R2 → ∞ divergiert die Induktionsspannung Umax . Gleichzeitig geht die Zeitskala gegeben durch τ ,
in welche der Strom durch die Spule abnimmt, gegen Null. Da nahezu die gesamte Induktionsspannung auch an
dem geöffneten Schalter abfällt, kann die Abwesenheit von R2 in der Praxis zu Funken- oder Lichtbogenbildung
an den Schalterkontakten führen.
II.
MAGNETISCHE REIBUNG
1. Das untere Leiterstück verlässt das Magnetfeld gleich zu Beginn des Falls, und die beiden senkrechten Stücke
bewegen sich in Richtung ihrer Längsachse. Somit wird in ihnen keine Spannung induziert, die zu einem
Stromfluss führt. Es bleibt das obere Leiterstück, das sowohl das Magnetfeld senkrecht schneidet als auch
senkrecht zu seiner Längsachse bewegt wird. In ihm wird eine Spannung Uind = vBl induziert. Im Leiter mit
dem Widerstand R fließt somit der Strom Iind = Uind /R.
2. Der Stromfluss führt im Magnetfeld zu einer senkrecht nach oben gerichteten magnetischen Kraft vom Betrag
FL = Iind lB. Desweiteren wirkt die Gravitationskraft FG = mg.
3. Somit lautet die Bewegungsgleichung für die Leiterschleife unter dem Einfluß beider Kräfte
m
dv
B 2 l2 v
= |FG + FL | = mg − Iind lB = mg −
dt
R
(4)
2
Wir führen die Konstante α ein, um im folgenden Schreibarbeit zu sparen:
α=
B 2 l2
mR
(5)
und somit
dv
B 2 l2 v
=g−
= g − αv
dt
mR
Wir integrieren mittels Separation der Variablen:
(
)
∫ t
∫ v
dv
1
1
αv
dτ =
−→ t = − (ln (g − αv) − ln (g)) = − ln 1 −
α
α
g
0
0 g − αv
(6)
(7)
Auflösen nach v ergibt
v=
dx
g
= (1 − e−αt )
dt
α
(8)
4. Für t → ∞ erhalten wir die maximale Grenzgeschwindigkeit v0 = g/α = 2.7 mm/s unter Verwendung der
angegebenen Zahlenwerte. Die Flugdauer nach der v um nur 1% von dieser Geschwindigkeit abweicht ergibt
sich aus v = 0.99v0 zu τ = −ln(0.01)/α = 1.3 · 10−3 s. Da diese Zeit sicherlich viel kleiner ist als die gesuchte
Flugzeit (vgl. mit freiem Fall) können wir die Geschwindigkeit der Leiterschleife in guter Näherung durch die
Grenzgeschwindigkeit approximieren: v(t) = v0 .
5. Damit ergibt sich für die gesuchte Zeit, nach der die Leiterschleife
das Magnetfeld verlässt t = l/v0 = 36 s. Zum
√
Vergleich: Im Fall B = 0 beträgt die Flugzeit nur tF = 2l/g = 0.1 s.