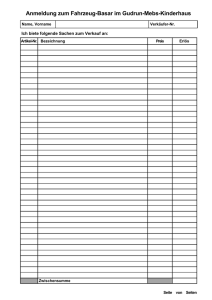
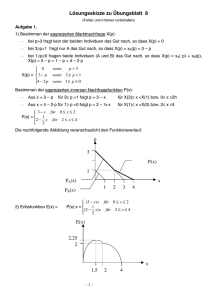
Economical Functions Deutsche Version.nb

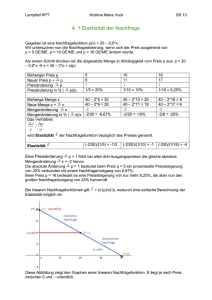
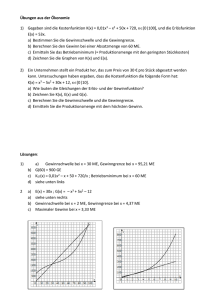
Economical Functions Deutsche Version.nb
1
Mathematics,Physics
and Economics using
E-learning Software
Thema: Wirtschaftsfunktionen
Adrian Micsa und Udo Stelzer
Berechnungen
Öffnen ê Schließen
Drucken
ü Funktionen
Öffnen ê Schließen
Die Kostenfunktion
Die betriebswirtschaftliche Kostenfunktion fasst alle entstehenden Kosten für eine bestimmte Menge x eines Produktes
zusammen. Sie enthält in der Regel fixe und variable Kosten.
Beispiel:
Die Firma ALUSTA GesmbH produziert Stahlbehälter für Schrauben und führt zu diesem Zwecke eine
Kostenrechnung. Es wird dazu eine Kostenfunktion verwendet:
K@x_D = 0.1 x3 − x2 + 4 x + 5;
Economical Functions Deutsche Version.nb
2
Plot@K@xD, 8x, 0, 12<, PlotStyle → Red,
AxesLabel → 8"Menge in Stk", "Kosten in Euro"<D;
Kosten in Euro
80
60
40
20
Menge in Stk
2
4
6
8
10
12
Wenn das Unternehmen nun zB 12 Stück Stahlbehälter produziert, dann fallen zunächst die Fixkosten an, die
unabhängig davon entstehen, ob oder wieviele Autos produziert werden (z.B. Miete für die Produktionshalle).
Weiterhin kommen die variablen Kosten dazu, die für jedes produzierte Auto genau einmal entstehen (z.B. pro Auto
Kosten für einen Motor).
Desto mehr man produziert, des höhere Kosten fallen an. Am Anfang steigen die Kosten nur langsam, da man für
geringere Produktionsmengen nur wenigere Arbeiter etc braucht. Jedoch ab einer gewissen Produktionsmenge steigen
die Kosten sprunghaft an da man um größere Mengen produzieren zu können mehere Arbeiter (z.B. eine 2. Schicht an
Arbeitern) etc einsetzten muss.
Preis
A) Fixpreis:
p@x_D = 5;
Die ALUSTA GesmbH verkauft ihre Ware mit einem Preis von € 5.00,- Der Preis von 5 ist fix, er ändert sich nicht, egal
wie viel man verkauft.
B) Variable Preisfunktion:
p@x_D = −0.5 x + 10
10 − 0.5 x
Das Unternehmen kalkuliert ihre Ware auch mit einer variablen Preisfunktion. Der Preis ist hier nicht fix, er ist
veränderbar.
a) Erlösfunktion mit Fixpreis
Economical Functions Deutsche Version.nb
3
Erl@x_D = p@xD ∗ x
5x
Der Erlös für das Unternehmen ergibt sich aus dem Preis (hier 5) mal der Menge (x).
Plot@Erl@xD, 8x, 0, 12<, PlotStyle → Black,
AxesLabel → 8"Menge in Stück", "Erlös in Euro"<D;
Erlös in Euro
60
50
40
30
20
10
Menge in Stück
2
4
6
8
10
12
Diese Grafik ist eine lineare Funktion. An dieser Grafik kann man den Ertrag im Verhältniss zur verkauften Menge
ablesen.
z.B sollte die ALUSTA GesmbH 12 Stück Stahlbehälter verkaufen, so wird ein Erlös von € 60.00,- erwirtschaftet
B) Erlösfunktion mit Preisfunktion
Erl@x_D = p@xD ∗ x êê Expand
10 x − 0.5 x2
Dies ist eine variable Preisfunktion.
k = 10;
Economical Functions Deutsche Version.nb
4
Plot@p@xD, 8x, 0, 20<, PlotStyle → Orange,
AxesLabel → 8"Menge in Stück", "Preis in Euro"<D;
Preis in Euro
10
8
6
4
2
Menge in Stück
5
10
15
20
Plot@Erl@xD, 8x, 0, 20<, PlotStyle → Blue,
AxesLabel → 8"Menge in Stück", "Erlös in Euro"<D;
Erlös in Euro
50
40
30
20
10
Menge in Stück
5
10
15
20
Bei der variablen Preisfunktion nimmt der Erlös ab einer bestimmten Menge ab. Nachdem ein Maximalerlös erzielt
wurde, nimmt der Erlös ab. Das hängt damit zusammen, dass ab einer bestimmten Produktionsmenge der Erlös die
Kosten nicht mehr decken kann und dass fast kein, bis gar kein Erlös erwirtschaftet wird.
A) Break Even Point mit Fixpreis
Erklärung Break Even Point:
Der Break-Even-Point ist der Punkt, an dem der Erlös und die Kosten einer Produktion gleich sind und damit weder
Verlust noch Gewinn erwirtschaftet werden. Dieser Punkt wird als Untere Gewinnschwelle bezeichnet. Wird die
Gewinnschwelle überschritten, erreicht man die Gewinnzone (man wird einen Gewinn machen), hingegen wird bei
Economical Functions Deutsche Version.nb
5
Unterschreitung ein Verlust erzielt.
Plot@8K@xD, Erl@xD<, 8x, 0, 12<, PlotStyle → 8Red, Black<,
AxesLabel → 8"Menge in Stück", "Kosten und Erlös in Euro"<D;
Kosten und Erlös in Euro
80
60
40
20
Menge in Stück
2
4
6
8
10
12
Rot: Kostenfunktion
Schwarz: Erlösfunktion
Punkte wo sich die beiden Kurven schneiden sind die Gewinnschwellen. An diesen beiden Punkten wird weder Gewinn,
noch Verlust gemacht.
Berechnung der Unteren und Oberen Gewinschwelle bei einem fixen Preis:
NSolve@G@xD == 0D
88x → −2.44594<, 8x → 1.94707<, 8x → 10.4989<<
Bei einem Verkauf von ca 2 Stücken Stahbehältern (Untere Gewinnschwelle) und bei einem Verkauf von ca 11 Stücken
Stahlbehältern (Obere Gewinnschwelle) wird kein Gewinn (Der Gewinn ist der Überschuss über die Aufwendungen)
erwirtschaftet. Ab einem Verkauf von 3 - 10 Stücken wird ein Gewinn erzielt. Je weiter sich der Kostengraph vom
Erlösgraph entfernt, desto mehr Gewinn wird erwirtschaftet. Werden jedoch weniger als 2 Stücke verkauft, so muss
man mit einem Verlust rechnen.
B)Break Even Point mit variabler Preisfunktion
Economical Functions Deutsche Version.nb
6
Plot@8K@xD, Erl@xD<, 8x, 0, 12<, PlotStyle → 8Red, Blue<,
AxesLabel → 8"Menge in Stück", "Erlös in Euro"<D;
Erlös in Euro
80
60
40
20
Menge in Stück
2
4
6
8
10
12
Rot: Kostenfunktion
Blau: Erlösfunktion
Berechnung der Unteren und Oberen Gewinschwelle bei einer variablen Preisfunktion:
NSolve@G@xD == 0D
88x → −6.12622<, 8x → 0.789584<, 8x → 10.3366<<
Bei der variablen Preisfunktion wird bei einem Verkauf von ca einem Stück (Untere Gewinnschwelle) und bei einem
Verkauf von ca 10 Stücken (Obere Gewinnschwelle) kein Gewinn erwirtschaftet. Das hat zur Folge, dass die
Gewinnzone breiter ist als bei der fixen Preisfunktion.
a) Movie mit fixem Preis
Mehr… ;
Clear@f, x, a, kD;
f@x_D = k ∗ x ; H∗ enter your f ∗L
MDMovie@ Plot@ 8f@xD, K@xD<, 8x, 0, 15<,
AxesLabel → 8"Menge", "Erlös"<, PlotRange → 80, 120<,
PlotLabel → "Preis = " <> ToString@NumberForm@k, 85, 3<DD <> "\n"D, 8k, 2, 8, 0.05<D;
Null
Economical Functions Deutsche Version.nb
7
Preis = +02.000
Erlös
120
100
80
60
40
20
Menge
2
4
6
8
10
12
14
Movie mit variabler Preisfunktion
Mehr… ;
Clear@f, x, a, kD;
f@x_D = Erl@xD ; H∗ enter your f ∗L
MDMovie@ Plot@ 8K@xD, f@xD<, 8x, 0, 15<, PlotRange → 80, 80<,
PlotLabel → "Preis = " <> ToString@NumberForm@k, 85, 3<DD <> "\n"D, 8k, 2, 8, 0.5<D;
Preis = +02.000
y
80
70
60
50
40
30
20
10
2
4
6
8
10
12
14
x
Gewinnfunktion:
Der Gewinn ist der Überschuss über die Aufwendungen.
G@x_D = Erl@xD − K@xD
−5 + 6 x + 0.5 x2 − 0.1 x3
Dies ist eine Gewinnfunktion die von der ALUSTA GesmbH. verwendet wird
Economical Functions Deutsche Version.nb
8
Plot@G@xD, 8x, 0, 12<, PlotStyle → Orange,
AxesLabel → 8"Menge in Stück", "Erlös in Euro"<D
Erlös in Euro
20
10
Menge in Stück
2
4
6
8
10
-10
-20
-30
Graphics Berechnung des Maximalgewinnes
NSolve@G '@xD == 0D
88x → −0.467251<, 8x → 7.13392<<
[email protected]
16.7202
Der Maximalgewinn befindet sich bei 7.13392 und beträgt 16,72 Euro pro Stück.
Drucken
Neu
Schließen
Ausschneiden
Schließen
12
Economical Functions Deutsche Version.nb
9
Das Projektteam
Öffnen ê Schließen
Drucken
Udo Stelzer, 17
Klasse 3cJ BHAK Leibnitz/Austria
E-Mail: [email protected]
Adrian Micsa, 17
Klasse 3cJ BHAK Leibnitz/Austria
E-Mail: [email protected]
Neues Kapitel
Kapitel löschen
Öffnen ê Schließen
Drucken
Erzeuge deinen eigenen surfing GUIDE für Mathematik!
Internet schließen
Schließen