Übertragungsfunktion RLC-Bandpass: komplex und mit FFT

R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 1/6
Passiver Bandpass (RLC-Schaltung). Berechnung der
komplexen Übertragungsfunktion mit zwei Methoden:
mit komplexer Rechnung und mit FFT
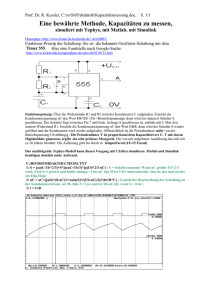
Bandpass aus 1 T-Glied: Z1= R1+ L1+RL1+ C1, Y1= Ck parallel (Lk+RLk)
Z2= L2+RL2+ C2m,
Y2= RA
Vgl Schaltung Nr 3.17 auf Homepage:
http://www.home.hs-karlsruhe.de/~kero0001/aufst6/AufstDGL6hs.html#3.17
R0
L1
i1
u0
K
C1
u1
Lk
RLk
L2
i2
ik
Ck
uk
C2
u2
RA
uA
6 Energiespeicher
C1, C2, Ck, L1, L2, Lk
6 Zustandsvariablen
u1, u2, uk, i1 , i2, ik
Der vorliegende Text berechnet die komplexe Übertragungsfunktion Ausgang zu
Eingang nach zwei verschiedenen Methoden:
Zunächst mit der „direkten“ Methode der komplexen Wechselstrom-Rechnung.
Dann mit Hilfe von der numerischen Fourier-Transformation (FFT): Auf den Eingang wird eine kurzer Impuls
gegeben (in Form einer Glockenkurve). Sowohl von der zeitlichen Ausgangsfunktion (Impulsantwort) als auch
von der zeitlichen Eingangsfunktion wird die FFT berechnet. Der komplexe Quotient FFT des Ausgangs
dividiert durch die FFT des Eingangs wird als gepunktete Kurven gemeinsam aufgetragen mit den Kurven der
komplexen Rechnung (durchgezogene Kurven). Dabei Auftragung Betrag und Phase als Funktion der Frequenz
und auch als komplexe Ortskurve (Imaginärteil als Funktion des Realteils mit Frequenz als Parameter).
Vergleicht man die durchgezogenen Kurven (also die „exakte“ Berechnung mittels komplexer Rechnung) mit
den gepunkteten Rechenwerten (FFT-Methode), so erkennt man weitgehende Übereinstimmung beider
Berechnungs-Methoden, falls gewisse Voraussetzungen eingehalten werden: Die Zeitdauer tmax muss
hinreicheichend lang sein, so dass die Impulsantwort weitgehend auf Null abgeklungen ist. Weiterhin muss der
Eingangsimpuls hinreichend kurz sein. (Diese Bedingung wird allerdings im vorliegende Text noch nicht
untersucht).
R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 2/6
Zunächst tmax hinreichend groß: Es ergeben sich nur wenig Unterschiede der
durchgezogenen Kurven (komplexe Methode) verglichen mit den gepunkteten Kurven
(FFT-Methode)
bild=1,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.1
u0/10
0.08
uAp
0.06
0.04
0.02
0
-0.02
-0.04
-0.06
0
20
40
60
80
100 sec120
140
160
180
200
bild=1,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.6
abs(u2)
Winkel(u2)
0.5
0.4
0.3
0.2
0.1
0
-0.1
-0.2
0
0.5
1
1.5
2
2.5
omega, FFT-Methode gepunktet
0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4
-0.4
-0.2
0
0.2
0.4
0.6
komplexe Ortskurve, FFT-Methode gepunktet
3
3.5
R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 3/6
Anschließend tmax kleiner : Die Amplituden-Kurven (schwarz) sind noch ziemlich
gleich, aber in den Phasenkurven (rot) deutliche Fehler sichtbar. In der Ortskurve sind
allerdings noch keine Unterschiede erkennbar, erst beim Zoomen der Ortskurve in der
Nähe des Nullpunktes sieht man die Unterschiede.
bild=5,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.1
u0/10
uAp
0.05
0
-0.05
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,150,1, 5 );
-0.1
0
50
sec
100
150
bild=5,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.6
abs(u2)
Winkel(u2)
0.4
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,150,1, 5 );
Da tmax(=150) zu klein, starker Phasenfehler, allerdings
in einem Bereich, wo die Amplitude schon sehr klein ist
0.2
0
-0.2
0
0.5
1
1.5
2
2.5
3
omega, FFT-Methode gepunktet
3.5
4
4.5
0.4
Hier ist der Physenfehler nicht sichtbar,
0.2 denn er ist nur bei sehr kleinen Amplituden vorhanden
0
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,150,1, 5 );
-0.2
-0.4
-0.4 Ortskurve,
-0.2
0 FFT-Methode
0.2
0.4 gepunktet
0.6
komplexe
R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 4/6
Anschließend tmax noch kleiner, so dass die Ausgangsfunktion noch nicht genügend
abgeklungen ist. Folglich stärkerer Fehler: In der Ortskurve sind jetzt Unterschiede
auch ohne Zoomen sichtbar.
bild=10,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.1
u0/10
uAp
0.05
0
tmax nur 100, das ist zu kurz, denn die Schwingung
ist noch nicht genügend abgeklungen
-0.05
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,110,1, 10 );
-0.1
0
20
40
60
sec
80
100
120
bild=10,R1=0.15,L1=1,RL1=0,C1=1,Lk=0.02,RLk=0,Ck=50,L2=1,RL2=0,C2=1,fak=1
0.6
abs(u2)
Winkel(u2)
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,110,1, 10 );
0.4
hier tmax nur 110, folglich noch stärkerer Phasenfehler,
auch im Bereich, wo Amplituden noch nicht sehr klein
0.2
0
-0.2
0
1
2
3
4
omega, FFT-Methode gepunktet
5
6
0.4
BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,110,1, 10 );
0.2
0
hier tmax nur 110, folglich Phasenfehler und Amplitudenfehler
-0.2 in Ortskurve erkennbar
-0.4
-0.4 -0.2
0
0.2
0.4
0.6
komplexe Ortskurve, FFT-Methode gepunktet
function BaPa1T14(R1, C1,L1,RL1, Lk,RLk,Ck, C2,L2,RL2,fak,dw, wmax,dt,tmax,DT,bild );
%BaPa1T14(R1, C1,L1,RL1, Lk,RLk,Ck, C2,L2,RL2,fak, dw,wmax,dt,tmax,DT,bild );
%BaPa1T14(0.15,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.01, 3, 0.01,200,1, 1 );
%BaPa1T14(1.1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0.01, 5, 0.01,200,1, 5 );
%BaPa1T14(0.6, 1, 1, 0, 0.25,0, 4, 1, 1, 0, 1, 0.01, 5, 0.01,200,1, 1 );
%BaPa1T14(0.35,1, 1, 0, 0.1, 0, 10, 1, 1, 0, 1, 0.01, 5, 0.01,200,1, 10 );
%BaPa1T14(0.25,1, 1, 0, 0.05,0, 20, 1, 1, 0, 1, 0.01, 3, 0.01,200,1, 15 );
R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 5/6
%BaPa1T14(0.5,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.01, 3, 0.01,200,1, 25 );
%BaPa1T14(0.05,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,200,1, 30 );%tmaxzuklein
%BaPa1T14(0.05,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,300,1, 35 );%tmaxnochzuklein
%BaPa1T14(0.05,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,400,1, 40 );%jetztfastok
%BaPa1T14(0.05,1, 1, 0, 0.02,0, 50, 1, 1, 0, 1, 0.001, 3, 0.01,400,1, 45 );
%BaPa1T14(0.6, 1, 1, 0, 0.25,0, 4, 1, 1, 0, 1, 0.01, 5, 0.01,200, 5 );
%BaPa1T14(0.35,1, 1, 0, 0.1, 0, 10, 1, 1, 0, 1, 0.01, 5, 0.01,200, 10 );
%
%
% Datei BaPa1T10.m
%BaPa1T1(R1, C1,L1,RL1, Lk,RLk,Ck, C2,L2,RL2,fak, dw,wmax,bild );
%BaPa1T1(0.25,1, 1, 0, 0.05,0, 20, 1, 1, 0, 1, 0.01, 3, 5 );
%R1=0.25; C1=1;L1=1;RL1=0;Lk=0.05;RLk=0;Ck=20; C2=1;L2=1;RL2=0;fak=1;
%dw=0.01;wmax=3; bild=1;
%dt=0.01; tmax=50;
%tmax=200;
% Auch Zeitbereich
% Bandpass aus 1 T-Glied:
% Z1= R1+ L1+RL1+ C1
% Y1= Ck parallel (Lk+RLk)
% Z2= L2+RL2+ C2
% Y2= RA
%
format compact;
w=1e-5:dw:wmax; % Vektor Kreisfrequenz w
s = j * w; % j = Wurzel aus (-1), s= "DiffenrentialOperator"
% Definition der Schaltung der 2-gliedrigen Kette:
Z1=R1+RL1 + s*L1 +1 ./(s*C1); % 1. LängsImpedanz
Y1= s*Ck+ 1 ./( RLk+ s*Lk ); % 1. QuerLeitWert
Z2= s*L2 + RL2 +1 ./( s*C2); % 1. LängsImpedanz
Y2= 1/(fak*R1);
% 2. QuerLeitWert
%
Y1p = Y1+ 1./(Z2+ 1./Y2); % ErsatzLeitWert parallel zu u1
u1=1 ./(1+ Z1 .* Y1p); % u1= Spannung am 1. QuerLeitWert
u2=u1 ./(1+ Z2 .* Y2); % u2= Spannung am 2. QuerLeitWert
%
S0=['bild=',num2str(bild)];
S1=[',R1=',num2str(R1)];S2=[',L1=',num2str(L1)];
S3=[',RL1=',num2str(RL1)];
S4=[',C1=',num2str(C1)];S5=[',Lk=',num2str(Lk)];
S6=[',RLk=',num2str(RLk)];S7=[',Ck=',num2str(Ck)];
S8=[',L2=',num2str(L2)];S9=[',RL2=',num2str(RL2)];
S10=[',C2=',num2str(C2)];S11=[',fak=',num2str(fak)];
Ti=[S0,S1,S2,S3,S4, S5,S6,S7,S8,S9,S10,S11];
figure(bild); clf reset;
plot(w, abs(u2),'k', w, angle(u2)*180/pi/1000,'m');
grid on; Title(Ti);
xlabel('omega');
legend('abs(u2)','Winkel(u2)');
% Ortskurve:
figure(bild+1); clf reset;
plot(real(u2),imag(u2)); axis equal;
grid on;
%xlabel('real(u2)');ylabel('imag(u2)');
%disp(' BaPa1T1(R1, C1,L1,RL1, Lk,RLk,Ck, C2,L2,RL2,fak, dw, wmax, bild ');
% Jetzt Zeitbereich
% dt=0.01; tmax=20;
t=0:dt:tmax; % Zeitvektor
uAp=zeros(1,length(t));
R. Kessler, C:\ro\Si05\Andy\komptep\Bandpass_FFT_3.doc, S. 6/6
%Startwerte:
i1=0; uC1=0; ik=0; uCk=0;
i2=0; uC2=0;
t1=5;
t2=t1+DT;
a0=0.9;
%uR= a0*(t>t1).*(t2>t); % EingangsSpannung Rechteckimpuls
u0= a0* exp(-(t-t1).*(t-t1)/(t2-t1)^2); % EingangsSpannung Glockenimpuls
% u0=uR+uG;
for k=1:length(t);
% Plotwerte speichern:
%uCkp(k)=uCk;
%uC1p(k)=uC1;
%uC2p(k)=uC2;
uAp(k)=fak*R1*i2;
% neue Werte berechnen:
i1=i1+(u0(k) -(R1+RL1)*i1-uC1-uCk)*dt/L1;
uC1=uC1+i1*dt/C1;
ik=ik+(uCk-RL1*ik)*dt/Lk;
uCk=uCk+(i1-ik-i2)*dt/Ck;
i2=i2+(uCk-uC2-i2*(RL2+fak*R1))*dt/L2;
uC2=uC2+i2*dt/C2;
end; % for k=1....
fftu0=fft(u0,length(t));
fftuAp=fft(uAp,length(t));
xfer=fftuAp ./ fftu0;
df=1/tmax;
freq=0:df: df*(length(t)-1);
figure(bild+2); clf reset;
%plot(t,u0, t, uAp, t,uCkp,t,uC1p, t,uC2p); grid on; xlabel('sec');
plot(t,u0/10,'m', t, uAp,'k'); grid on; xlabel('sec');title(Ti);
legend('u0/10','uAp')
FuAp=fft(uAp,length(uAp)); Fu0=fft(u0,length(t)); xfer=FuAp./Fu0;
% neu 21.5.07
figure(bild); hold on;
plot(2*pi*freq(1:100),abs(xfer(1:100)),'.k',...
2*pi*freq( 1:100),angle(xfer(1:100))*180/pi/1000,'.m');
hold off;
figure(bild+1); hold on;
plot( real(xfer(1:100)), imag(xfer(1:100)),'.'); % FFT-Methode gepunktet
disp('BaPa1T14(R1,C1,L1,RL1, Lk,RLk,Ck, C2,L2,RL2,fak, dw,wmax,dt,tmax,DT,bild )');
% Ende Datei BaPa1T14.m