Blatt 6

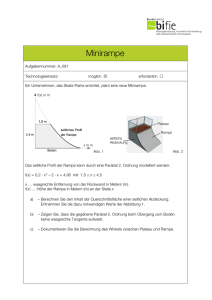
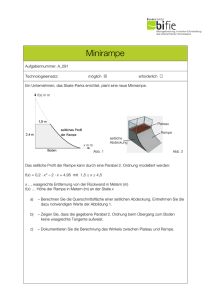
A. Bittracher
Programmierpraktikum: Numerik von ODEs (MA9502)
Übungsblatt 6
01. Juni 2015
Aufgabe 8 (Freier Fall mit Luftreibung)
Wir wollen die Bewegung eines Körpers mit Position x ∈ R2 modellieren. Auf den
Körper wirke zum einen die Gravitationskraft (in x2 -Richtung), zum anderen die
Luftwiderstandskraft.
Die Bewegung wir durch Netwon’s zweites Gesetz F = m · a beschrieben. Dabei ist
m die Masse des Körpers, F die Gesamtkraft und a die Beschleunigung des Körpers.
Die Gesamtkraft ist F = FG + FR , mit
Symbol Größe
SI-Einheit
Gravitationskraft
F
Kraft
kg · m/s2
v
Geschwindigkeit
m/s
0
FG = m
a
Beschleunigung
m/s2
−g
m
Masse
kg
und Luftwiderstandskraft
g
Fallbeschleunigung
m/s2
cW
Luftwiderstandskoeff. ohne
1
FR = − cW Aρkvk2 v .
A
Angriffsfläche
m2
2
ρ
Luftdichte
kg/m3
Die Größen x, v, a und F sind dabei vektorwertig zu verstehen.
(a) Beschreiben Sie die Bewegung des Körpers durch ein Differentialgleichungssystem zweiter Ordnung.
(b*) Schreiben Sie das System aus (a) als Differentialgleichungssystem erster Ordnung. Implementieren Sie seine rechte Seite in Matlab als
function [y] = freierfall_rs(t,x),
so dass die Matlab-Standardlöser (z.B. ode45) leicht darauf anwendbar sind.
(c) Realistische Werte für einen Fallschirmspringer sind m = 80, g = 9.81, cw = 1.35,
A = 25, ρ = 1.2. Ermitteln Sie experimentell (z.B. mit ode45) die Endgeschwindigkeit des Fallschirmspringers.
Aufgabe 9 (Springender Ball)
Wir nehmen den Körper aus der vorherigen
Aufgabe jetzt als Ball an und lassen ihn aus
einiger Höhe auf eine lineare Rampe fallen. Die
Rampe verbindet die Punkte (0, 1) und (1, 0),
und setzt sich bis ins Unendliche fort.
Beim Aufprall auf die Rampe soll der Geschwindigkeitsvektor umgelenkt werden (Eintrittswinkel = Austrittswinkel) und leicht gedämpft werden.
x2
1
x1
1
(a) Den Aufprall behandeln wir in Matlab mit so genannten Events. Machen Sie
sich mit dem Event Handling von ode45 vertraut. Schauen Sie sich dazu nochmals Aufgabe A16 aus NumODE, sowie das in Matlab enthaltene Beispiel
ballode an.
Dokumentation: ODE Event Location
(b*) Schreiben Sie eine Eventfunktion
function [value,isterminal,direction] = event_rampe(t,y),
die das Auftreffen auf der Rampe erkennt, d.h. die val=0 genau dann zurückgibt, falls y auf der Rampe liegt. Der Löser soll bei erkanntem Event terminieren
(isterminal=1). Achten Sie darauf, auch direction korrekt zu setzen!
(c*) Schreiben Sie damit ein Programm, das den Ball auf der Rampe simuliert.
Wir lassen den Ball von Position (0, 2) fallen. Beim Auftreffen auf die Rampe
soll ode45 gestoppt werden. Der Geschwindigkeitsvektor des Balls soll dann
angepasst werden (Dämpfungsfaktor 0.7). Anschließend soll ode45 mit den
neuen Anfangswerten re-initiiert werden, um den weiteren Verlauf der Flugbahn
zu simulieren.
Die weiteren Parameter sind m = 1, g = 9.81, cW = 1, A = 0.2, ρ = 1.2.
Lassen Sie den Ball 5 mal springen. Visualisieren Sie die Bewegung des Balls
mit einen Trajektorienplot.
Abgabedatum: 06.06.2015
Die Lösungen der mit (*) markierten Aufgaben sind bis zum Abgabedatum an
[email protected] zu senden. Verwenden Sie den Betreff ProgODE und erwähnen Sie in der Email Ihre Matrikelnummer!