16. Platonische Körper — kombinatorisch - TU Wien

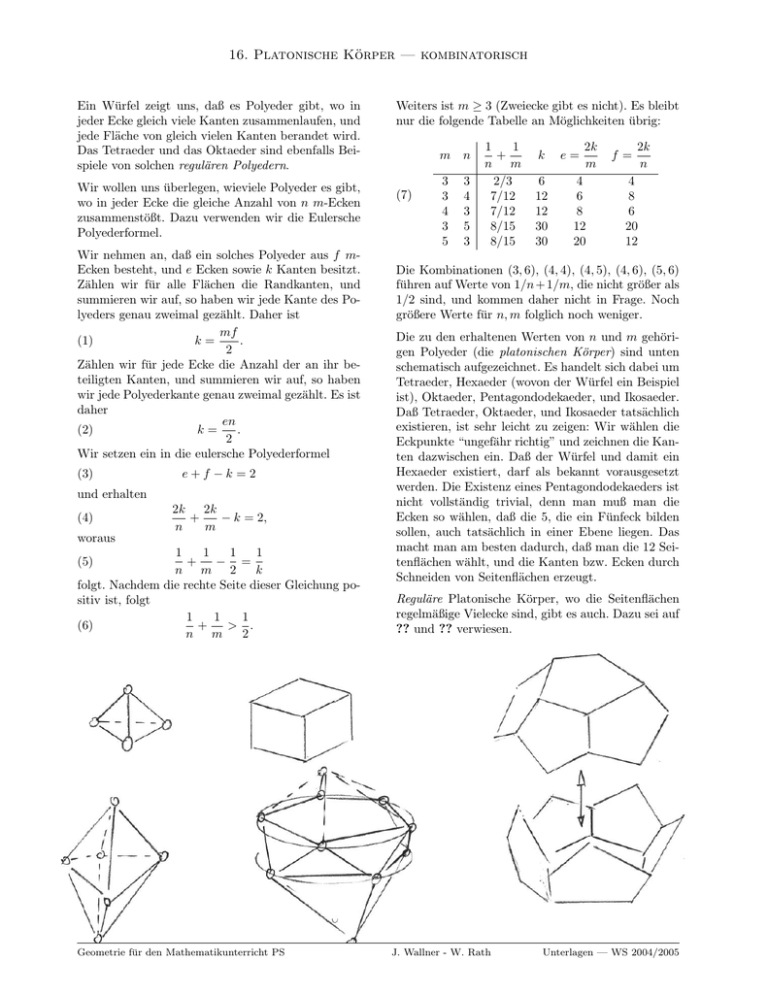
16. Platonische Körper — kombinatorisch
Ein Würfel zeigt uns, daß es Polyeder gibt, wo in
jeder Ecke gleich viele Kanten zusammenlaufen, und
jede Fläche von gleich vielen Kanten berandet wird.
Das Tetraeder und das Oktaeder sind ebenfalls Beispiele von solchen regulären Polyedern.
Wir wollen uns überlegen, wieviele Polyeder es gibt,
wo in jeder Ecke die gleiche Anzahl von n m-Ecken
zusammenstößt. Dazu verwenden wir die Eulersche
Polyederformel.
Wir nehmen an, daß ein solches Polyeder aus f mEcken besteht, und e Ecken sowie k Kanten besitzt.
Zählen wir für alle Flächen die Randkanten, und
summieren wir auf, so haben wir jede Kante des Polyeders genau zweimal gezählt. Daher ist
mf
.
(1)
k=
2
Zählen wir für jede Ecke die Anzahl der an ihr beteiligten Kanten, und summieren wir auf, so haben
wir jede Polyederkante genau zweimal gezählt. Es ist
daher
en
(2)
k=
.
2
Wir setzen ein in die eulersche Polyederformel
(3)
e+f −k =2
und erhalten
(4)
2k 2k
+
− k = 2,
n
m
woraus
1
1
1
1
+
− =
n m 2
k
folgt. Nachdem die rechte Seite dieser Gleichung positiv ist, folgt
1
1
1
(6)
+
> .
n m
2
(5)
Geometrie für den Mathematikunterricht PS
Weiters ist m ≥ 3 (Zweiecke gibt es nicht). Es bleibt
nur die folgende Tabelle an Möglichkeiten übrig:
(7)
m
n
3
3
4
3
5
3
4
3
5
3
1
1
+
n m
2/3
7/12
7/12
8/15
8/15
k
6
12
12
30
30
e=
2k
m
4
6
8
12
20
f=
2k
n
4
8
6
20
12
Die Kombinationen (3, 6), (4, 4), (4, 5), (4, 6), (5, 6)
führen auf Werte von 1/n + 1/m, die nicht größer als
1/2 sind, und kommen daher nicht in Frage. Noch
größere Werte für n, m folglich noch weniger.
Die zu den erhaltenen Werten von n und m gehörigen Polyeder (die platonischen Körper) sind unten
schematisch aufgezeichnet. Es handelt sich dabei um
Tetraeder, Hexaeder (wovon der Würfel ein Beispiel
ist), Oktaeder, Pentagondodekaeder, und Ikosaeder.
Daß Tetraeder, Oktaeder, und Ikosaeder tatsächlich
existieren, ist sehr leicht zu zeigen: Wir wählen die
Eckpunkte “ungefähr richtig” und zeichnen die Kanten dazwischen ein. Daß der Würfel und damit ein
Hexaeder existiert, darf als bekannt vorausgesetzt
werden. Die Existenz eines Pentagondodekaeders ist
nicht vollständig trivial, denn man muß man die
Ecken so wählen, daß die 5, die ein Fünfeck bilden
sollen, auch tatsächlich in einer Ebene liegen. Das
macht man am besten dadurch, daß man die 12 Seitenflächen wählt, und die Kanten bzw. Ecken durch
Schneiden von Seitenflächen erzeugt.
Reguläre Platonische Körper, wo die Seitenflächen
regelmäßige Vielecke sind, gibt es auch. Dazu sei auf
?? und ?? verwiesen.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
17. Die Platonischen Körper metrisch I
Wir suchen unter den Tetraedern, Hexaedern, Oktaeder, Ikosaedern, und Pentagondodekaeders ‘metrisch reguläre’ Vertreter, deren Seiten regelmäßige Vielecke gleicher Größe sind. Wir werden den
Würfel, das reguläre Hexaeder, zur Konstruktion
weiterer regulärer Polyeder benützen.
Punkte
Oktaeder und Tetraeder Verbindet man die 6
Flächenmitten eines Würfels mit 12 Kanten, so entstehen 8 gleichseitige Dreiecke, also ein reguläres Oktaeder. Wählt man von den 8 Ecken eines Würfels
4 aus, sodaß nie 2 benachbart sind, und verbindet
man diese durch 6 Flächendiagonalen, so entstehen
4 gleichseitige Dreiecke, also ein reguläres Tetraeder.
(2)
Ikosaeder Will man die Konstruktion schriftlich beschreiben, tut man das am besten über Koordinaten:
Wir betrachten den Würfel mit Ecken (±1, ±1, ±1)
aus und zeichnen in dessen Seitenflächen die 12
Geometrie für den Mathematikunterricht PS
(1)
(±1, 0, ±α), (±α, ±1, 0), (0, ±α, ±1)
ein (0 < α < 1). Verbindet man jeden dieser Punkte mit seinen 5 nächsten Nachbarn, z.B. den Punkt
(1, 0, α) mit
(1, 0, −α), (α, ±1, 0), (0, ±α, 1),
so erhält man ein Ikosaeder mit zwei verschiedenen
Typen von Kanten. Deren Längen sind
(3)
(4)
k(1, 0, α) − (1, 0, −α)k = 2α,
p
k(1, 0, α) − (α, 1, 0)k = (1 − α)2 + 1 + α2 .
Alle Kanten sind gleich lang, wenn
p
2α = (1 − α)2 + 1 + α2 , d.h.
√
(5)
α = ( 5 − 1)/2 = 0.61803398874 . . .
√
Bemerkung: Die Zahl ( 5 − 1)/2 ist goldene Schnitt.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
18. Die Platonischen Körper metrisch II: Das Dodekaeder
Pentagondodekaeder Wir wollen uns davon überzeugen, daß es ein reguläres Pentagondodekaeder
gibt, d.h. einen Körper, der von 12 regulären Fünfecken berandet wird, sodaß in jeder Ecke drei Fünfecke zusammenstoßen. Eine Abwicklung einer solchen polyhedralen Flächen in die Ebene läßt sich
leicht angeben (siehe Figur). Biegt man die fünf 5ecke rund um ein Fünfeck auf und klebt sie entlang
ihrer Seiten aneinander, so ensteht ein ‘Korb’. Zwei
solcher Körbe lassen sich zu einem Pentagondodekaeder zusammensetzen. Die Frage ist nur: Warum
passen zwei solche Körbe ineinander? Wir werden
das Problem anders lösen, nämlich indem wir auf
jede Seitenfläche eines Würfels (dessen Existenz als
bekannt vorausgesetzt wird), ein Dach errichten, und
zwar so, daß immer zwei Dachflächen, die entlang einer Würfelkante zusammentreffen, miteinander ein
reguläres Fünfeck bilden (siehe Figur).
√
Sei b = ( 5 − 1)/2 (der goldenen Schnitt), und sei 1
die Länge der Würfelkante. Ein Dach sei durch die
in der Figur unten angegebenen Abmessungen festgelegt. Wir nehmen nun sechs Dächer und setzen sie
wie unten angegeben auf die 6 Würfelseiten.
Geometrie für den Mathematikunterricht PS
Es sind nun folgende Dinge zu zeigen: (i) zwei Dachflächen, die entlang einer Würfelkante zusammentreffen, liegen in einer gemeinsamen Ebene, (ii) alle
Kanten des so entstehenden Polyeders haben dieselbe Länge, und (iii) die entstehenden Fünfecke sind
regelmäßig (dies kann etwa durch Längengleichheit
ausreichend vieler Diagonalen gezeigt werden).
Um (i) nachzuweisen, müssen wir α + β = 90◦ (siehe Figur) zeigen. Dies folgt aus der Ähnlichkeit der
beiden rechtwinkeligen Dreiecke mit Katheten 1/2,
b/2, sowie mit Katheten b/2, (1−b)/2, die man leicht
nachrechnen kann: (1/2) : (b/2) = (b/2) : ((1−b)/2).
(ii) besteht aus mehrmaligem Anwenden des Satzes des Pythagoras: Es ist tatsächlich ((1 − b)/2)2 +
(1/2)2 + (b/2)2 = b2 , also haben alle Kanten die
Länge b.
(iii) Ein Fünfeck kann lauter gleiche Kanten haben,
ohne regulär zu sein. Wenn alle Diagonalen gleich
lang sind, ist das Fünfeck regelmäßig. Es reicht aber
zu zeigen, dass die Diagonale eines Fünfecks, die auf
einer Würfelkante liegt, und die Diagonalen des Trapezes, das eine Dachfläche bildet, gleich lang sind.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
19. Flächeninhalt von sphärischen Dreiecken
Auf einer Kugel wird die Rolle der Geraden von den
Großkreisen eingenommen. Das sind Kreise, deren
Ebenen durch den Kugelmittelpunkt gehen. Zwei
Punkte, die einander nicht gegenüberliegen, haben
immer einen eindeutigen Großkreis als kürzeste Verbindung. Sind drei Punkte A, B, C auf einer Kugel gegeben, so teilen die drei Großkreisbögen a, b, c,
die dadurch bestimmt sind, die Kugel in acht Teile.
Der kleinere davon heißt das sphärische Dreieck mit
Ecken A, B, C und Seiten a, b, c (wir wählen die Bezeichnungen hier so, daß immer Ecke und gegenüberliegende Seite durch den gleichen Buchstaben bezeichnet werden). Die Innenwinkel bei A, B, C seien
α, β, γ.
Wir betrachen ein sphärischen Zweieck mit Öffnungswinkel α: Es ist begrenzt durch zwei Großkreisbögen, die einen Winkel α einschließen. Alle
Großkreisbögen im Inneres dieses Winkels gehören
zum Zweieck dazu. Für α = π erhalten wir eine Halbkugel als Zweieck, und im Grenzfall α = 2π (die beiden Großkreisbögen fallen zusammen) erhalten wir
die Vollkugel.
Die Fläche A eines sphärischen Zweiecks ist offenbar linear proportional zum Öffnungswinkel. Nachdem die Oberfläche der Vollkugel (α = 2π) bekannt
ist und 4πr2 beträgt, haben wir A = 2αr2 . Für ein
sphärisches Dreieck ABC teilen die Großkreise die
die Seiten a, b, c tragen, die Kugel in insgesamt 8
Geometrie für den Mathematikunterricht PS
Dreiecke
(1)
ABC, ABC 0 , AB 0 C, A0 BC,
A0 B 0 C, A0 BC 0 , AB 0 C 0 , A0 B 0 C 0
(siehe Figur). Dabei sind A0 , B 0 , C 0 die A, B, C gegenüberliegenden Punkte. Zwei dieser Dreiecke, zum
Beispiel ABC und A0 BC, können einander zu einem
sphärisches Zweieck ergänzen, das in diesem speziellen Fall den Öffnungswinkel α besitzt. Insgesamt
können wir also die folgenden Gleichungen für die
Flächeninhalte der 8 Dreiecke hinschreiben:
ABC + A0 BC = 2αr2
ABC + AB 0 C = 2βr2
ABC + ABC 0 = 2γr2
A0 B 0 C 0 + AB 0 C 0 = 2αr2
A0 B 0 C 0 + A0 BC 0 = 2βr2
A0 B 0 C 0 + A0 B 0 C = 2γr2
Addiert man diese 6 Gleichungen, so ist die Summe der Dreiecke aus Gl. (??) gleich 4πr2 , und wir
erhalten
2ABC + 2A0 B 0 C 0 + 4πr2 = 4αr2 + 4βr2 + 4γr2
Die Flächen von ABC und A0 B 0 C 0 sind gleich, die
beiden Dreiecke gehen auseinander durch Spiegelung
am Kugelmittelpunkt hervor. Es folgt also für die
Fläche des Dreiecks ABC der Wert
r2 (α + β + γ − π).
Damit ist auch gezeigt, daß die Winkelsumme eines sphärischen Dreiecks nicht 180◦ beträgt, sondern
abhängig von der Fläche größer als 180◦ ist.
J. Wallner - W. Rath
Unterlagen — WS 2004/2005
20. Winkelsummen in der euklidischen und sphärischen Geometrie
Satz 1. In der euklidischen Geometrie ist die Winkelsumme im Dreieck gleich 180◦ .
Beweis. siehe untenstehende Skizze.
Satz 2. In der sphärischen Geometrie ist die Winkelsumme im Dreieck gleich π + A/r2 , mit A als
Fläche des Dreiecks
Beweis. In Nr. ?? wurde für den Flächeninhalt der
Wert (α + β + γ − π)r2 hergeleitet, wobei α, βγ die
Innenwinkel sind.
Um allgemein eine Aussage über die Winkelsumme
in einem n-Eck zu erhalten, betrachten wir den Exzeß eines Vielecks: Dieser ist definiert aus Summe der
Innenwinkel minus π(n − 2). Die obige Aussage über
die Winkelsumme eines Dreiecks in der euklidischen
Ebene kann man auch so formulieren, daß sein Exzeß
gleich Null ist. Der Exzeß ist gleichermaßen für euklidische und für sphärische Vielecke definiert. Nach
Satz ?? ist der Exzeß in einem sphärischen Dreieck
gleich A/r2 .
Macht man aus einem n-Eck ein (n + 1)-Eck, indem
man eine Seite durch einen neuen Eckpunkt unterteilt, so erhöht sich die Winkelsumme um π, die Anzahl der Ecken um 1, der Exzeß bleibt gleich (siehe
Figur).
Satz 3. Zerlegt man ein n-Eck durch eine Strecke
in ein n1 -Eck und ein n2 -Eck, und sind S, S1 und
S2 die entsprechenden Winkelsummen, so gilt
S1 + S2 = S.
Beweis. Betrachen wir eine Ecke, die sowohl dem
n1 -als auch dem n2 -Eck gemeinsam ist, dann ist
die Summe der Innenwinkel des n1 -und des n2 -Ecks
gleich dem Innenwinkel des n-Ecks an dieser Stelle.
Für die Winkelsummen S1 , S2 und S des n1 -, des
n2 -, und des n-Ecks gilt also S1 + S2 = S.
Geometrie für den Mathematikunterricht PS
Satz 4. Der Exzeß ist additiv, d.h. zerlegt man ein
n-Eck durch eine Strecke in ein n1 -Eck und ein n2 Eck, und sind e,e1 und e2 die entsprechenden Ezxesse, so gilt
e1 + e2 = e.
Beweis. Offenbar ist n = n1 + n2 − 2, denn in es gibt
genau 2 Ecken, die sowohl dem n-Ecke, als auch dem
n1 -Eck und dem n2 -Eck angehören. Damit ist
e1 + e2
= S1 − (n1 − 2)π + S2 − (n2 − 2)π
= S − (n − 2)π = e.
Satz 5. Die Winkelsumme in einem n-Eck in der
euklidischen Ebene beträgt (n − 2)π. Der Exzeß ist
gleich Null.
Beweis. Es genügt zu zeigen, daß der Exzeß gleich
Null ist. Wir können jedes n-Eck durch eine Strecke
in Vielecke kleinerer Eckenzahl zerteilen. Nachdem
der Exzeß sich dabei additiv verhält, und wir bereits
wissen, daß der Exzeß für Dreiecke gleich Null ist,
gilt dies auch für Vierecke, 5-Ecke, etc., d.h. für alle
n-Ecke.
Satz 6. Die Winkelsumme in einem n-Eck auf einer Kugel vom Radius r ist gleich A/r2 + (n − 2)π,
wobei A die Fläche ist. Der Exzeß ist gleich A/r2 .
Beweis. Es genügt offenbar, e = A/r2 zu zeigen. Für
Dreiecke gilt diese Gleichung. Wir können jedes nEck durch eine sphärische Strecke (d.h. einen Großkreisbogen) in Vieleck kleinerer Eckenzahlen n1 , n2
unterteilen. Wir führen einen Induktionsbeweis: Angenommen, wir hätten den Satz für n1 -und n2 -Ecke
bereits gezeigt. Seien A1 , A2 die Flächen der beiden
Teile. Dann ist A1 + A2 = A und e1 + e2 = e. Es
folgt
e = e1 +e2 = A1 /r2 +A2 /r2 = (A1 +A2 )/r2 = A/r2 .
J. Wallner - W. Rath
Unterlagen — WS 2004/2005