Stromverdrängung in rechteckigen Leitern (z. B

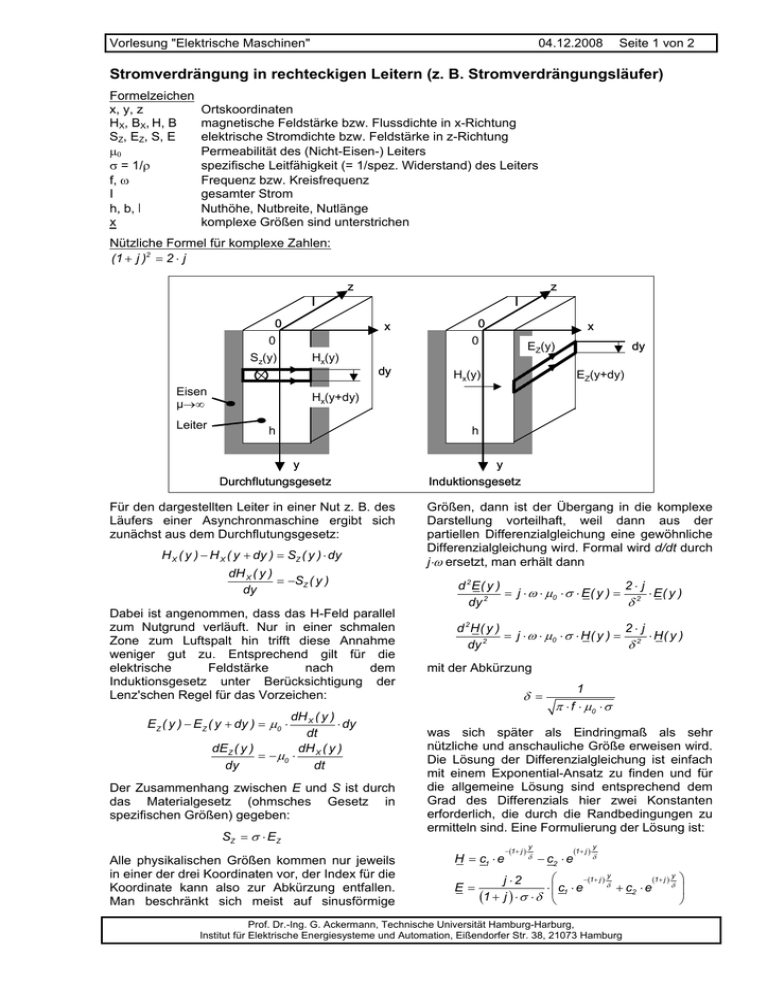
Vorlesung "Elektrische Maschinen"
04.12.2008
Seite 1 von 2
Stromverdrängung in rechteckigen Leitern (z. B. Stromverdrängungsläufer)
Formelzeichen
x, y, z
HX, BX, H, B
SZ, EZ, S, E

 = 1/
f, 
I
h, b, l
x
Ortskoordinaten
magnetische Feldstärke bzw. Flussdichte in x-Richtung
elektrische Stromdichte bzw. Feldstärke in z-Richtung
Permeabilität des (Nicht-Eisen-) Leiters
spezifische Leitfähigkeit (= 1/spez. Widerstand) des Leiters
Frequenz bzw. Kreisfrequenz
gesamter Strom
Nuthöhe, Nutbreite, Nutlänge
komplexe Größen sind unterstrichen
Nützliche Formel für komplexe Zahlen:
(1  j )2  2  j
z
z
l
0
l
0
x
0
Sz(y)
Hx(y)
Eisen
μ
Leiter
0
x
dy
EEZ(y)
Z(y)
Hx(y)
dy
EZ(y+dy)
Hx(y+dy)
h
h
y
Durchflutungsgesetz
Für den dargestellten Leiter in einer Nut z. B. des
Läufers einer Asynchronmaschine ergibt sich
zunächst aus dem Durchflutungsgesetz:
H X ( y )  H X ( y  dy )  SZ ( y )  dy
dH X ( y )
 SZ ( y )
dy
Dabei ist angenommen, dass das H-Feld parallel
zum Nutgrund verläuft. Nur in einer schmalen
Zone zum Luftspalt hin trifft diese Annahme
weniger gut zu. Entsprechend gilt für die
elektrische
Feldstärke
nach
dem
Induktionsgesetz unter Berücksichtigung der
Lenz'schen Regel für das Vorzeichen:
dH X ( y )
 dy
dt
dEZ ( y )
dH X ( y )
  0 
dy
dt
EZ ( y )  EZ ( y  dy )  0 
Der Zusammenhang zwischen E und S ist durch
das Materialgesetz (ohmsches Gesetz in
spezifischen Größen) gegeben:
SZ    EZ
Alle physikalischen Größen kommen nur jeweils
in einer der drei Koordinaten vor, der Index für die
Koordinate kann also zur Abkürzung entfallen.
Man beschränkt sich meist auf sinusförmige
y
Induktionsgesetz
Größen, dann ist der Übergang in die komplexe
Darstellung vorteilhaft, weil dann aus der
partiellen Differenzialgleichung eine gewöhnliche
Differenzialgleichung wird. Formal wird d/dt durch
j ersetzt, man erhält dann
d 2 E( y )
2 j
 j    0    E( y )  2  E( y )
2
dy

d 2 H( y )
2 j
 j    0    H( y )  2  H( y )
2
dy

mit der Abkürzung
 
1
  f  0  
was sich später als Eindringmaß als sehr
nützliche und anschauliche Größe erweisen wird.
Die Lösung der Differenzialgleichung ist einfach
mit einem Exponential-Ansatz zu finden und für
die allgemeine Lösung sind entsprechend dem
Grad des Differenzials hier zwei Konstanten
erforderlich, die durch die Randbedingungen zu
ermitteln sind. Eine Formulierung der Lösung ist:
H  c1  e
E
1 j 
y

 c2  e
j 2

1
 j    
1 j 
y

y
y
1 j 

1 j  

  c1  e
 c2  e  


Prof. Dr.-Ing. G. Ackermann, Technische Universität Hamburg-Harburg,
Institut für Elektrische Energiesysteme und Automation, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung "Elektrische Maschinen"
04.12.2008
Am Nutgrund muss H = 0 sein. Nimmt man den
gesamten Strom I als gegeben an (wenn andere
Größen gegeben sind ändert sich alles nur um
eine Konstante), dann ist bei y = 0 durch das
Durchflutungsgesetz Hb = I die zweite Gleichung
gegeben. Die Konstanten c1 und c2 sind somit
aus
folgenden
beiden
Gleichungen
zu
bestimmen:
0  c1  e
1 j 
h
 c2  e

1 j 
I
c2  
b
e
e
1 j 
h
e
1 j 
1 j 
1 j 
h

e
h

h

1 j 
h

Für eine sehr niedrige Frequenz und damit
verbunden ein sehr großes Eindringmaß kann
man die e-Funktionen approximieren nach
ex  1+x.
Dann
folgt
nach
wenigen
Umrechnungen aus diesen Gleichungen der
bekannte lineare Verlauf:
H( y )  H(0 ) 
hy
h
Für die elektrische Feldstärke folgt der bekannte
Zusammenhang entsprechend der Berechnung
des ohmschen Widerstandes eines langen
geraden Leiters:
j 2
1  j     
y

   c1  c2    c1  c2   1  j   


E
j 2
1

 j    
 H(0 )  
y
 
 H(0 )  1  j   

 1  j   h
E
I
b  h 
E
Wesentlich informativer ist der Fall einer sehr
(unendlich) tiefen Nut. Dann muss c2 = 0 sein,
anderenfalls würden die Feldgrößen unendlich.
H  H(0 )  e
1 j 
y

y

U  E  
j 2
I
 
1  j      b
U  (1  j ) 

I
   b
Der Stab entspricht also einer Reihenschaltung
eines Widerstandes mit einer Induktivität, wobei
der Widerstand genau durch den mit dem
Eindringmaß gebildeten Querschnitt bestimmt ist.
Man kann also ersatzweise annehmen, dass der
Strom in einer Schicht mit der Dicke 
konzentriert ist. Die Reaktanz der Induktivität ist
ebenso groß wie der ohmsche Widerstand,
deshalb ist die Phasenverschiebung genau 45°.

h

e
e
1 j 
Die Spannung längs des Stabes, die man mit
einem Voltmeter vom Luftspalt her messen
könnte, folgt aus Feldstärke für y = 0:
h
Das ergibt:
I
c1  
b
gegenüber der Oberfläche beträgt 1 rad, also
klingt die von der Oberfläche eindringende Welle
bereits in weniger als ¼ Periode auf 1/e ab.

I
 c1  c2
b
Seite 2 von 2
I 1 j 
e
b
E
j 2
I 1 j 
 e
1  j      b
S
j 2
I 1 j 
 e
1  j    b
y
y
Daraus wird jetzt nachträglich die Bedeutung des
Eindringmaßes  klar: In der Tiefe  hat der
Betrag aller Größen um den Faktor 1/e
abgenommen.
Die
Phasenverschiebung
Zahlenwerte:
Kupfer:
 = 9,5 mm für 50 Hz
Aluminium:
  13 mm für 50 Hz
Eisen (r >> 1)  bei 0,1 mm für 50 Hz
Ergänzung:
a) Die angeführten Gleichungen gelten in
ähnlicher Form auch für den Fall, dass das
Magnetfeld und nicht der Strom eingeprägt ist.
Daraus ist deutlich, warum Magnetkerne für
wechselnde Magnetfelder nicht aus massivem
Eisen sein dürfen, das Magnetfeld würde ja nur in
der obersten Schicht entsprechend dem sehr
kleinen Eindringmaß verlaufen. Bei elektrischen
Maschinen werden die Kerne aus gegeneinander
isolierten Blechen von 0,25 mm bis 0,35 mm
(seltener 0,5 mm) aufgebaut. Da das Magnetfeld
an beiden Oberflächen verläuft, durchsetzt das
Feld dieses dünne Blech praktisch vollkommen.
b) Ab Frequenzen von wenigen kHz müssten die
Bleche unpraktikabel dünn sein. Man verwendet
dann
Ferrit,
einen
Sinter-Werkstoff
aus
"Eisenkrümeln", der kaum elektrisch leitet
(=> Eindringmaß groß), aber leider auch eine
kleinere Permeabilität und eine kleinere
Sättigungsflussdichte als Eisenblech hat.
c) Die hier angeführten Gleichungen sind immer
dann anwendbar, wenn das Eindringmaß
wesentlich kleiner ist als die geometrische
Abmessung. Im entgegengesetzten Fall kann die
Stromverdrängung
ohnehin
vernachlässigt
werden. Der Übergangsbereich ist nur selten von
praktischem Interesse. Wenn eine Schätzung
zwischen
unendlicher
und
sehr
kleiner
Eindringtiefe nicht ausreicht, dann sind oft auch
andere Randeffekte von erheblicher Bedeutung
und man setzt numerische Rechenverfahren ein.
Prof. Dr.-Ing. G. Ackermann, Technische Universität Hamburg-Harburg,
Institut für Elektrische Energiesysteme und Automation, Eißendorfer Str. 38, 21073 Hamburg