Hans Walser, [20090207a] Folgen im Schachbrett 1 Harmonische

Hans Walser, [20090207a]
Folgen im Schachbrett
1
Harmonische Folgen
1.1 Konstruktion
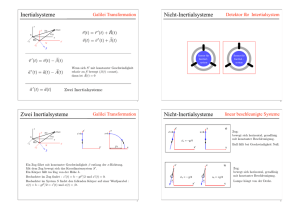
Wir beginnen mit Gitterpunkten im Schachbrett und zeichnen eine Zickzack-Linie, deren Ecken zu harmonischen Folgen führen.
Start
Die folgende Figur zeigt den ersten Schritt der Konstruktion der Zickzack-Linie.
Erster Schritt
2/4
Hans Walser: Folgen im Schachbrett
Nun folgen weitere Schritte. An den Rändern sind die relativen Höhen der Eckpunkte
der Zickzack-Linie im Vergleich zur Seitenlänge des Schachbrettes vermerkt. Diese
Höhen lassen sich mit einem geeigneten Koordinatensystem berechnen.
1
2
3
1
2
2
5
1
3
1
4
2
7
2
9
Weitere Schritte
Am linken Rand erkennen wir die klassische harmonische
1, 12 , 13 , 14 ,… = 1n n . Der Beweis lässt sich induktiv führen.
Was hat es mit den Zahlen am rechten Rand auf sich?
{
} {
}
Folge
1.2 Das harmonische Mittel
Unter dem harmonischen Mittel h zweier Zahlen a und b verstehen wir:
m = 121
a
+b
Beispiel: Ein Autorennfahrer fährt die erste Runde (der Länge s) mit der Geschwindigkeit v1 und die zweite Runde mit der Geschwindigkeit v2 . Wie groß ist die Durchschnittsgeschwindigkeit in diesen ersten beiden Runden zusammen?
Bearbeitung: Für die erste Runde ist ein Zeitaufwand t1 = vs erforderlich, entsprechend
1
für die zweite Runde t 2 =
s
v2
. Die Durchschnittsgeschwindigkeit vh ist also:
vh = t 2s
=
1 +t 2
2s
s + s
v1 v2
=
2
1+ 1
v1 v2
Wir erhalten das harmonische Mittel der beiden einzelnen Geschwindigkeiten. Die Länge s des Rennringes spielt keine Rolle.
3/4
Hans Walser: Folgen im Schachbrett
1.3
Harmonische Folgen
{
} {
}
In der klassischen harmonischen Folge 1, 12 , 13 , 14 ,… = 1n n ist jedes Folgenglied
das harmonische Mittel der beiden Nachbarglieder. Wir reden nun allgemein von einer
harmonischen Folge {an } , wenn an+1 = 1 2 1 . Unter diesem Aspekt bilden auch die
Zahlen
{
}={
2 , 2 , 2 , 2 ,…
3 5 7 9
2
2n+1
an
}
+a
n+2
n am rechten Rand eine harmonische Folge, eben-
so die Folge, dies sich aus der Vereinigung der beiden Folgen ergibt:
{1, 23 , 12 , 25 , 13 , 27 , 14 , 28 ,…} = { 22 , 23 , 24 , 25 , 26 , 27 , 28 , 28 ,…} = { 2n n \ {1}}
Aus der Definitionsbedingung an+1 =
1
an
2
+a
ergibt sich die Rekursionsformel:
1
n+2
an+2 =
1
2 1
an+1 an
Wegen dem Minuszeichen im Nenner kann es zu einer Division durch Null kommen.
Bei den Startwerten a1 = 1 und a2 = 2 etwa muss man mit Gefühl arbeiten:
n
1 2
3
4
5
6
an 1 2 2 1 23
Bei den Startwerten a1 = 1 und a2 = 3 tritt der Pol nicht auf:
n
1 2
3
4
5
6
7
8
9
3 3
an 1 3 3 1 53 73 13 11
13
4/4
Hans Walser: Folgen im Schachbrett
2
Geometrische Folgen
2.1 Konstruktion
Wir beginnen mit Gitterpunkten im Schachbrett und zeichnen eine Zickzack-Linie, deren Ecken zu geometrischen Folgen führen.
Erster Schritt
1
1
2
1
4
1
8
1
32
1
16
Weitere Schritte
Es entsteht eine geometrische Folge. Der Beweis ergibt sich aus den Strahlensätzen.