Mitschrift S. 160 - 178

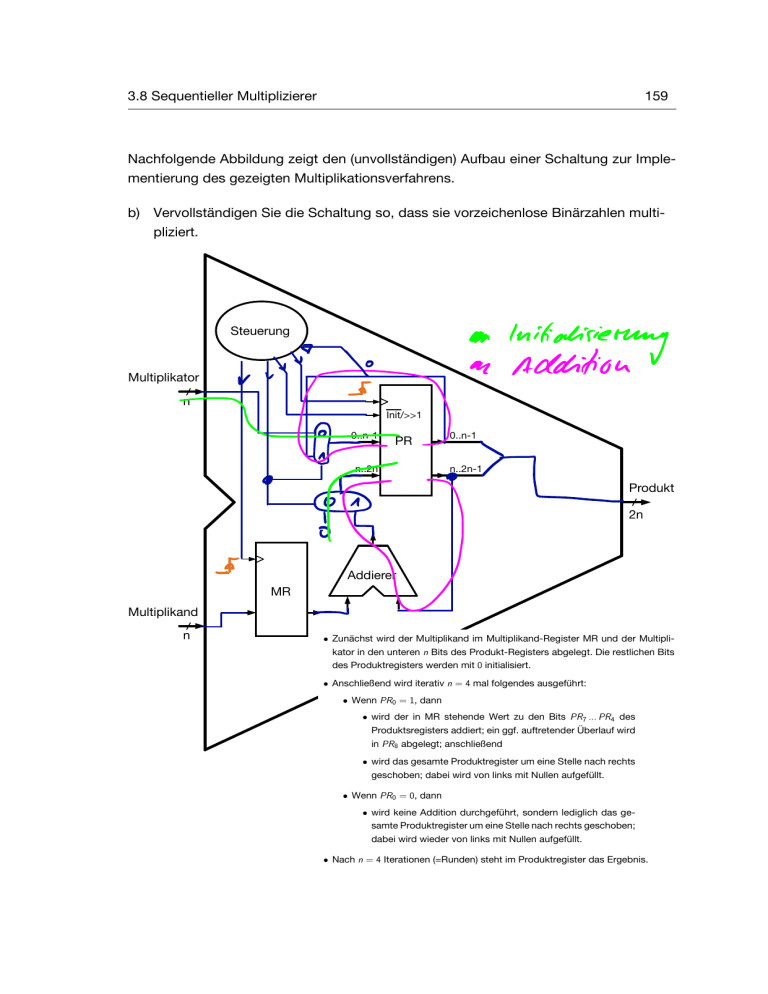
3.8 Sequentieller Multiplizierer
159
Nachfolgende Abbildung zeigt den (unvollständigen) Aufbau einer Schaltung zur Implementierung des gezeigten Multiplikationsverfahrens.
b) Vervollständigen Sie die Schaltung so, dass sie vorzeichenlose Binärzahlen multipliziert.
¥-1
:#
:
¥1
Steuerung
Multiplikator
3.7 Multiplizierer
n
141
aämäiää
Init/>>1
a-
Sequentielle
Multiplikation vorzeichenloser Zahlen
0..n-1 Schaltung zur 0..n-1
PR
In
Mit einer sequentiellen Schaltung kann der Hardwareaufwand deutlich reduziert werden.
Die nächste Abbildung skizziert eine sequentielle Schaltung, die zur Multiplikation von
n..2n
n..2n-1
vorzeichenloser Zahlen der Wortbreite n = 4 verwendet werden kann:
MR
y3 y2 y1 y0
Add
⇒
PR
n
0
0
2n
PR0
0 x3 x2 x1 x0
Addierer
MR
Multiplikand
0 0
Produkt
Das Multiplikand-Register MR ist n = 4 Bit breit, das Produkt-Register PR ist 2n + 1 = 9
Bit breit.
PR0 ist das niederwertigste Bit des im Produktregister gespeicherten Werts.
Der Ablauf ist wie folgt:
• Zunächst wird der Multiplikand im Multiplikand-Register MR und der Multiplikator in den unteren n Bits des Produkt-Registers abgelegt. Die restlichen Bits
des Produktregisters werden mit 0 initialisiert.
• Anschließend wird iterativ n = 4 mal folgendes ausgeführt:
• Wenn PR0 = 1, dann
• wird der in MR stehende Wert zu den Bits PR7 ... PR4 des
Produktsregisters addiert; ein ggf. auftretender Überlauf wird
in PR8 abgelegt; anschließend
• wird das gesamte Produktregister um eine Stelle nach rechts
geschoben; dabei wird von links mit Nullen aufgefüllt.
• Wenn PR0 = 0, dann
• wird keine Addition durchgeführt, sondern lediglich das gesamte Produktregister um eine Stelle nach rechts geschoben;
dabei wird wieder von links mit Nullen aufgefüllt.
• Nach n = 4 Iterationen (=Runden) steht im Produktregister das Ergebnis.
160
c)
3 Arithmetische Schaltungen
Vervollständigen Sie nachfolgend abgebildeten Zustands-Automaten so, dass er
den Multiplizierer wie gewünscht steuert. Nehmen Sie an, dass Sie zur Detektion
des Schleifen-Abbruchs das Signal Runde_n zur Verfügung haben, das Ihnen
anzeigt, ob Sie bereits alle Runden durchlaufen haben (Runde_n = 1) oder noch
don't
×
nicht (Runde_n = 0).
Wert
Änis
Oo
öisfi
=
an
immer
-
.
1
Initialisierung
clk_mkand= 0
0
multiplexer= 0
init/>>1= 0
clk_produkt=
clk_produkt=
multiplexer=
4¥
1
×
init/>>1=
7
Ende
clk_mkand=
clk_produkt=
multiplexer=
init/>>1=
2
Initialisierung
clk_mkand= 1
1
-
.
3
Addieren
clk_mkand=
clk_produkt=
1
clk_produkt=
multiplexer=
0
multiplexer=
init/>>1= 0
Runden
6
Schieben
0
clk_mkand=
PRO
8
⇒
-0
5
Schieben
0
clk_mkand=
0
>
1
0
c)
4
Addieren
clk_mkand=
0
clk_produkt=
multiplexer=
multiplexer=
init/>>1=
init/>>1=
Runden
immer
0
init/>>1= 0
c) PRO
clk_produkt=
care
egal
=
>
"
"
"
"
-0ft
PRO
1
=
1
immer
3.8 Sequentieller Multiplizierer
161
Multiplexer-basierte Implementierung der Steuerung
Für den Fall n = 4 soll die Steuerung wie folgt implementiert werden:
clk_mkand
clk_produkt
multiplexer
Kombinatorische
Schaltung
init/>>1
3
...
clk
...
D0 Q0
D2 Q2
D3 Q3
D4 Q4
2
2
3
PR0
Das Zustandsregister speichert die Information über
• den aktuellen Zustand (d.h. in welchem Zustand des Zustandsdiagramms sich
die Steuerung gerade befindet) und
• den Rundenzähler (d.h. welche Iterations-Runde gerade ausgeführt wird).
a)
In welchen Bits des Zustandsregisters wird
• der aktuelle Zustand und
• die aktuelle Runde
gespeichert?
Zustand
Runde
:
:
Bib
Bib
2.
4.3
1,0
162
3 Arithmetische Schaltungen
b) Tragen Sie in nachfolgende Abbildung die Eingangswerte des Multiplexers ein, die
die Ausgangs-Funktion der Steuerung implementieren. Womit muss der Steuereingang des Multiplexers verbunden werden?
Aktueller
Zustand
3
(
0000
)4
0000
4
1100
4
0010
4
Uno
4
00×1
4
01×1
4
OOXX
4
0
1
2
3
clk_mkand
3
2
clk_produkt
1
multiplexer
0
init/>>1
4
5
6
7
4
3.8 Sequentieller Multiplizierer
c)
163
Tragen Sie in nachfolgende Abbildung diejenigen Eingangswerte ein, welche die
Zustands-Übergangs-Funktion aller unbedingter Verzweigungen implementieren.
Aktueller
Zustand
3
(
001
010
)
0
3
1
3
2
3
100
3
101
3
110
Folge
1
3
4
-
zustand
0
5
3
6
3
111
2
3
7
3
d) Tragen Sie in nachfolgende Abbildung ein Schaltung ein, die den Folgezustand
0
⇒
101
des Zustands 2 liefert.
PRO
1,1
=
PRO
=
1
011
⇒
±
PR0
>
d
1
2
,
0
3
Folgezustand
von Zustand 2
164
e)
3 Arithmetische Schaltungen
Tragen Sie in nachfolgende Abbildung eine Schaltung ein, die im Zustand 5 den
Eingang Runde um 1 erhöht und den neuen Rundenwert am Ausgang bereitstellt
(00 ! 01, 01 ! 10, 10 ! 11, 11 ! 00). In Zuständen 6= 5 soll die am Eingang
angelegte Runde an den Ausgang durchgereicht werden.
Zustand
(Bit 2 ... 0)
3
101,2
f.
Ito
ggf
81oiwomunftmtand.si
y.no
,
MAI
Runde
(Bit 4, 3)
f)
2
i
2
Neue Runde
(Bit 4, 3)
Tragen Sie in nachfolgende Abbildung eine Implementierung des Runde_nDetektors ein, der in Runde 1, 2 und 3 den Ausgang auf Low-Pegel legt und
in Runde 4 auf High-Pegel (Runde 1 , 01, Runde 2 , 10, Runde 3 , 11, Runde
4 , 00).
Runde
(Bit 4,3)
2
II.
i
1
Runde_n
3.8 Sequentieller Multiplizierer
165
g) Tragen Sie in nachfolgende Abbildung eine Multiplexer-basierte Schaltung ein, die
in Abhängigkeit der Eingänge Runde_n und PR0 den auf Zustand 6 folgenden
Zustand am Ausgang ausgibt.
Runde_n
1
7-8
Ä
PR0
h)
3
Folgezustand
von Zustand 6
1
Tragen Sie in nachfolgende Abbildung eine Schaltung ein, die den auf Zustand
6 folgenden Zustand mit Hilfe eines Inverters und zweier ODER-Gatter bestimmt
und am Ausgang ausgibt.
Runde_n
→
1
PR0
1
Runden
Runden
Runde
kl
-0
=
-
U
Oft
-1
3
10
1
µ✓
-
z
PRO
pro
0
=
=
Folgezustand
von Zustand 6
101
1
011
111
166
3 Arithmetische Schaltungen
ROM-basierte Implementierung der Steuerung
In diesem Abschnitt soll die Multiplizierer-Steuerung mit nachfolgend abgebildeter ROMbasierten Schaltung implementiert werden.
clk_mkand
clk_produkt
multiplexer
init/>>1
Q0
Q1
Q2
Q3
Q4
ROM
5 4 3 2 1 0
clk
D0
D1
D2
D3
D4
8 7 6 5 4 3 2 1 0
PR0
1
Initialisierung
clk_mkand= 0
immer
2
Initialisierung
clk_mkand= 1
PR0 = 1
3
Addieren
clk_mkand= 0
clk_produkt= 0
clk_produkt= 1
clk_produkt= 0
multiplexer= 0
multiplexer= 0
multiplexer= 1
init/>>1= 0
init/>>1= 0
init/>>1= 0
Runde_n = 0 && PR0 = 0
immer
PR0 = 0
6
Schieben
clk_mkand= 0
5
Schieben
clk_mkand= 0
4
Addieren
clk_mkand= 0
clk_produkt= 1
clk_produkt= 0
clk_produkt= 1
multiplexer= X
multiplexer= X
multiplexer= 1
init/>>1= 1
init/>>1= 1
immer
immer
Runde_n = 1
7
Ende
clk_mkand= 0
clk_produkt= 0
Runde_n = 0 && PR0 = 1
multiplexer= X
init/>>1= X
immer
init/>>1= 0
3.8 Sequentieller Multiplizierer
a)
167
Welche Organisation hat das ROM?
64×9
Bit
Im ROM wird durch die Adress-Bits 0, 1 und 2 der Zustand festgelegt, durch die
Adress-Bits 3 und 4 der Rundenzähler, der die Anzahl der Iterationen mitzählt.
Zum Start der Multiplikation wird das Zustandsregister mit [Q0, Q1] = [0, 0] und [Q2, Q3,
Q4] = [0, 0, 1] initialisiert, d.h. Runde 00, Zustand 001.
b) Geben Sie den ROM-Inhalt an, der zur Implementierung der Zustände 1 und 2
benötigt wird.
Daten
Adresse
PR0
c)
Zustand
00
001
1
00
001
0
00
010
1
00
010
Zust. 1
Zust. 2
Runde
÷
Ausgang
Folgerunde
Folgezust.
0000
00
010
0000
00
010
1100
00
101
1100
00
011
Geben Sie den Inhalt des ROM-Speichers für Zustand 3 an.
PR0
Zust. 3
Runde
Zustand
Ausgang
Folgerunde
Folgezust.
00
100
1
00
1
01
011
0010
01
100
1
10
011
0010
10
100
1
11
011
0010
11
100
0110010
168
3 Arithmetische Schaltungen
d) Geben Sie den Inhalt des ROM-Speichers für Zustand 4 an.
Zust. 4
e)
PR0
Runde
1
00
100
0110
00
101
1
01
100
0110
01
101
1
10
100
0110
10
101
1
11
100
UNO
11
101
Zustand
Ausgang
Folgerunde
Folgezust.
Geben Sie den Inhalt des ROM-Speichers für Zustand 5 an.
PR0
Zust. 5
Runde
Zustand
Ausgang
Folgerunde
Folgezust.
0
00
101
00×1
01
0
01
101
10
0
10
101
00×1
00×1
11
110
110
0
11
101
Von
00
110
110
110
1
00
101
00×1
01
1
01
101
10
1
10
101
00×1
00×1
11
1
11
101
00×1
00
110
110
110
3.8 Sequentieller Multiplizierer
f)
169
Geben Sie den Inhalt des ROM-Speichers für Zustand 6 an.
PR0
Zust. 6
Runde
0
00
0
01
0
Zustand
110
Ausgang
01×1
10
110
110
01×1
01×1
0
11
110
01×1
1
1
00
01
110
1
10
110
^
11
Folgerunde
00
01
10
11
11001×111
01×1
110 01×110
00
01×1
01
Folgezust.
111
101
101
101
111
011
011
011
g) Geben Sie den Inhalt des ROM-Speichers für Zustand 7 an.
PR0
Zust. 7
Runde
Zustand
Ausgang
Folgerunde
9881%88%88
Folgezust.
nun
170
3 Arithmetische Schaltungen
Multiplikation vorzeichenbehafteter Zahlen
Zur Multiplikation vorzeichenbehafteter Zahlen (2er-Komplement) kann auf die Schaltung
für vorzeichenlose Multiplikation zurückgegriffen werden, wenn negative Zahlen zuerst
negiert werden, das Vorzeichen separat berechnet wird (XOR) und das Ergebnis ggf.
noch invertiert wird.
Es gibt jedoch auch noch andere Verfahren wie z.B. den sog. Baugh-WooleyMultiplizierer. Dieser ist sehr ähnlich wie der kombinatorische Multiplizierer für vorzeichenbehaftete Zahlen aufgebaut, verwendet jedoch an einigen Stellen ein NICHTUND-Gatter statt eines UND-Gatters sowie einen zusätzlichen Halbaddierer für die
höherwertigste Ergebnis-Stelle.
Multiplikation von Gleitkomma-Zahlen
• Zur Multiplikation von Gleitkommazahlen müssen die Mantissen inkl. führender
‘‘1,’’ als Festkommazahlen multipliziert werden.
• Die Exponenten werden addiert. Der Offset ‘‘k’’ ist nach der Addition doppelt
berücksichtigt und muss deswegen vom Ergebnis noch einmal subtrahiert
werden.
• Zur Re-Normalisierung wird die Ergebnis-Mantisse nach rechts geschoben und
zum Exponenten die Anzahl der geschobenen Stellen addiert.
3.9 Subtraktion
171
3.9 Subtraktion
Allgemein
Bezeichnungen: Minuend - Subtrahend = Differenz
Die Subtraktion zweier Zahlen wird stellenweise ausgeführt. Dabei kann es vorkommen,
dass ein größerer Wert von einem kleineren Wert subtrahiert werden muss. Um dies zu
bewerkstelligen, kann aus der nachfolgenden Stelle ein Wert geborgt werden.
Beispiel:
11
2 + 1 1 + 1 11
4 3 2 1
- 1 2 3 4
= 3 0 8 7
• 4 und wieviel ist 1? ) geht nicht ) 1 von 10-er Stelle borgen ) aus 1 wird 11
• 4 und wieviel ist 11? ) 7
• Durch das Borgen steht an der Zehner-Stelle jetzt nur noch eine 1 statt einer 2
• 3 und wieviel ist 1? ) geht nicht ) 1 von 100-er Stelle borgen ) aus 1 an der
Zehner-Stelle wird 11
• 3 und wieviel ist 11? ) 8
• Durch das Borgen steht an der Hunderter-Stelle jetzt nur noch eine 2 statt einer
3
• 2 und wieviel ist 2? ) 0
• 1 und wieviel ist 4 ) 1
Statt beim Borgen die Minuenden-Stellen zu verkleinern, kann die Subtrahenden-Stelle
vergrößert werden (wie Übertrag).
4 3 2 1
- 1 2 3 4
0
1
1
= 3 0 8 7
Das Ergebnis ist das gleiche, da die Differenz zwischen Minuenden-Stelle und
Subtrahenden-Stelle gleich bleibt. Beim Borgen über mehrere Stellen hinweg kann
einem dieses Vorgehen jedoch leichter fallen.
172
:
a)
T
c)
3 Arithmetische Schaltungen
Subtrahieren Sie 11 - 6 = 5 im Binärsystem bei einer Wortbreite n = 4.
b) Subtrahieren Sie 12 - 5 = 7 im Binärsystem bei einer Wortbreite n = 4.
Subtrahieren Sie 14 - 11 = 3 im Binärsystem bei einer Wortbreite n = 4.
3.9 Subtraktion
173
Halb-Subtrahierer
Ein Halb-Subtrahierer ist ein Schaltung, die ein Eingangs-Bit yi von einem Eingangs-Bit
xi subtrahiert. Das Ergebnis ist ein Differenz-Bit di und ein Borge-Bit bi (b = borgen =
engl. borrow).
Eingang xi
Eingang yi
Borgen bi
Differenz di
0
0
1
1
0
1
0
1
0
1
0
0
0
1
1
0
Die Differenz di entspricht der XOR-Verknüpfung der Eingänge; bi hat den Wert 1, wenn
der Minuend 0 ist und der Subtrahend 1 ist.
xi
yi
xi
yi
HS
bi
bi
di
di
Halbsubtrahierer können Binärzahlen nur halb subtrahieren: Der Halbsubtrahierer an
Stelle i erkennt zwar, ob er ein Bit von Stelle i + 1 borgen musste, kann jedoch selbst
nicht berücksichtigen, ob der Halbsubtrahierer an Stelle i 1 von ihm selbst ein Bit
borgen musste.
3.10 Dividierer
174
157
3 Arithmetische Schaltungen
Voll-Subtrahierer
Voll-Subtrahierer
Im Gegensatz zum Halbsubtrahierer kann ein Vollsubtrahierer berücksichtigen, ob die
Im Gegensatz Stelle
zum Halbsubtrahierer
kann
ein Vollsubtrahierer berücksichtigen, ob die
vorangegangene
i 1 ein Bit borgen
musste.
vorangegangene Stelle i 1 ein Bit borgen musste.
a) Vervollständigen Sie nachfolgende Wertetabelle eines Vollsubtrahierers.
a) Vervollständigen
nachfolgende
Wertetabelle eines Vollsubtrahierers.
Tabelle,
die in die GrafikSie
eingebettet
wurde:
xi
yi
bi
0
0
0
0
0
1
1
1
1
0
1
0
11
1
1
0
1
1
11
00
1
0
0
00
1
1
0
1
00
00
1
1
0
00
00
1
1
1
bi
di
O
0
00
01
:
1
1
1
1
b) Tragen Sie in nachfolgende Abbildung (links) eine Implementierung einer
Vollsubtrahierer-Schaltung ein.
b) Tragen Sie in nachfolgende Abbildung (links) eine Implementierung einer
Ripple-Borrow-Subtrahierer
Vollsubtrahierer-Schaltung ein.
a)
Berechnen Siex537 - 48 im Dezimalsystem.
y
i
i
b) Berechnen Sie
c)
¥
xi
yi
Vervollständigen Sie nachfolgende Wertetabelle eines
b
idc
3.10 Dividierer
CI
di
.
Er
.
bi-1
bi
VS
di
bi-1
3.9 Subtraktion
175
Ripple-Borrow-Subtrahierer
Beim Ripple-Borrow Subtrahierer werden n Vollsubtrahierer so verschaltet, dass sich
damit die Differenz d = x y zweier n Bit breiter Zahlen berechnen lässt.
xn-1
x2
…
yn-1
xi
bi
x1
y2
…
yi
xi
VS bi-1
bi
y1
yi
xi
VS bi-1
di
dn-1
x0
bi
di
yi
xi
VS bi-1
di
d2
…
y0
bi
yi
VS bi-1
0
di
d1
d0
Betrachten Sie den Zahlenring für vorzeichenlose Zahlen.
1111
0000
1110
0001
15
1101
0
14
1
13
1100
1011
12
3
11
4
10
6
8
0100
Richtung
steigender
Werte
0101
7
1001
0110
1000
5
0011
5
9
1010
a)
0010
2
0111
Nehmen Sie an, die Eingangswerte des entworfenen Ripple-Borrow-Subtrahierers
sind vorzeichenlos. Welches Zahlenformat hat die Differenz d? Welche Funktion
hat das ‘‘Borrow Out’’?
176
3 Arithmetische Schaltungen
Betrachten Sie den Zahlenring für Zahlen im Zweier-Komplement:
1111
0000
1110
0001
-1
1101
0
-2
1
-3
1100
-4
3
negativ
1011
-5
4
1010
0011
positiv
-6
0100
5
-7
-8
7
1001
6
0101
0110
1000
7
0010
2
0111
b) Funktioniert der Subtrahierer auch mit dem Zweier-Komplement? Wenn ja: Wie
kann man einen Überlauf feststellen? Wenn nein: Warum nicht?
3.9 Subtraktion
7
c)
177
Tragen Sie in nachfolgende Abbildung eine Schaltung ein, die einen Überlauf von
Zahlen im Zweierkomplement feststellt.
xn-1
yn-1
dn-1
u