Titelei Schwabl 1

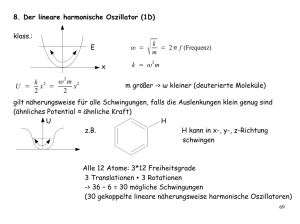
Vorwort zur fünften Auflage
Bei dieser Neuauflage wurden an einer Reihe von Stellen Ergänzungen angebracht; außerdem wurden am Ende der Kapitel Übungsaufgaben eingefügt.
Bei allen diesen Zusätzen habe ich versucht, den kompakten Charakter des
Buches nicht zu verändern. Bei dieser Gelegenheit möchte ich allen Mitarbeitern danken, die Verbesserungsvorschläge machten. Besonderer Dank gilt
Herrn Dr. S. Clar, der die Änderungen in den TEXfile einarbeitete.
München, im Januar 1998
F. Schwabl
Vorwort zur vierten Auflage
Erfreulicherweise wurde nach anderthalb Jahren eine weitere Neuauflage
notwendig. Bei dieser Gelegenheit wurden einige kleine Ergänzungen und
Korrekturen von Druckfehlern angebracht.
München, im Juni 1993
F. Schwabl
Vorwort zur dritten Auflage
Die erfreulich positive Aufnahme des Buches hatte zur Folge, daß die zweite Auflage innerhalb von zwei Jahren vergriffen war. In der vorliegenden Neuauflage wurden die Kapitel über Störungstheorie, zeitabhängige
Phänomene (Quantisierung des Strahlungsfeldes) und Meßprozeß erweitert
und an einigen Stellen kurze Ergänzungen eingefügt. Dabei wurde darauf Bedacht genommen, den kompakten Charakter des Buches nicht zu verändern.
Der Zuwachs der Seitenzahl rührt weniger von diesen Zusätzen her, als vielmehr von dem gegenüber der zweiten Auflage reduzierten Buchformat. Das
dadurch notwendige Lesen der Druckfahnen wurde von Frau M. Schiegl und
den Herren N. Knoblauch, J. Krumrey und W. Rossmann-Bloeck besorgt.
Ich danke ihnen sowie allen Kollegen, Mitarbeitern und Studenten, die Verbesserungsvorschläge machten.
München, im Januar 1992
F. Schwabl
Vorwort zur ersten Auflage
Das vorliegende Lehrbuch behandelt die Quantenmechanik. In einem einleitenden Kapitel werden, ausgehend von der historischen Entwicklung, an Hand
eines Interferenzexperiments die Grundpostulate erschlossen, von da ab ist
der Aufbau rein deduktiv. Neben den Grundlagen und vielen Anwendungen werden auch neue Aspekte der Quantentheorie und deren experimentelle
Überprüfungen dargestellt. Im Text wird Wert auf eine gestraffte Darstellung
gelegt, die dennoch keine weiteren Hilfsmittel erfordert. Die Verständlichkeit
wird gewährleistet durch Angabe aller mathematischen Schritte und ausführliche und vollständige Durchführung der Zwischenrechnungen.
Das Buch behandelt die nichtrelativistische Quantenmechanik ohne zweite Quantisierung, abgesehen von einem Abschnitt ,,Optische Übergänge”, der
eine elementare Darstellung der Quantisierung des Strahlungsfeldes enthält.
Neben dem unabdingbaren Stoff der Quantenmechanik, innerhalb dessen die
Streutheorie, zeitabhängige Phänomene und die Dichtematrix ausführlich diskutiert werden, enthält das Buch eine Darstellung der Theorie des Meßprozesses und der Bellschen Ungleichung. Ein Kapitel, das bisher noch nicht
Eingang in die Lehrbuchliteratur gefunden hat, ist die supersymmetrische
Quantenmechanik.
Aus didaktischen Gründen wird zunächst die Wellenmechanik entwickelt
und ab Kapitel 8 zur Dirac-Notation übergegangen. Nebenrechnungen und
Bemerkungen, die für das Verständnis nicht entscheidend sind, werden in
Kleindruck dargestellt. Nur in den etwas fortgeschritteneren Abschnitten sind
Zitate angegeben, die auch dort keineswegs vollständig sind, aber zur weiteren
Lektüre anregen sollen.
Das Buch wird Studenten der Physik und verwandter Fachgebiete ab dem
4. oder 5. Semester empfohlen, und Teile daraus können möglicherweise auch
von Lehrenden nutzbringend verwendet werden.
Dieses Buch ist aus Vorlesungen über Quantenmechanik, die der Autor
seit 1973 an der Universität Linz und der Technischen Universität München
gehalten hat, entstanden. Bei Teilen der Rohfassung des Skriptums und von
Zeichnungen und Tabellen haben die Herren R. Alkover, E. Frey und H.-T.
Janka mitgewirkt. Die Korrekturen der Druckfahnen wurden von den Herren
Th. Fischer, W. Prusseit, H. Schinz, A. Schorgg, S. Thoma und U. Täuber
gelesen. Herr W. Gasser hat das gesamte Manuskript gelesen und zu vielen
VIII
Vorwort zur ersten Auflage
Kapiteln des Buches wertvolle Anregungen gegeben. Ihnen und allen anderen
Mitarbeitern, deren Hilfe für die Entstehung wichtig war, sowie dem Verlag
sei an dieser Stelle herzlichst gedankt.
München, September 1988
F. Schwabl
3. Eindimensionale Probleme
In diesem Kapitel werden wir die Schrödinger-Gleichung für charakteristische
eindimensionale Potentiale lösen und einige typische Effekte der Quantenmechanik besprechen.
3.1 Der harmonische Oszillator
Die Hamilton-Funktion des klassischen harmonischen Oszillators (Abb. 3.1)
mit Masse m und Frequenz ω ist
H=
p2
mω 2 2
+
x .
2m
2
(3.1)
Mit Impulsoperator p stellt (3.1) den Hamilton-Operator dar. Die zeitunabhängige Schrödinger-Gleichung ist somit
~2 d 2
mω 2 2
x
−
+
ψ(x) = Eψ(x) ,
(3.2)
2m dx2
2
und enthält offensichtlich als charakteristische Länge
r
~
x0 =
.
ωm
(3.3)
Die Standardmethode der Analysis zur Lösung der Differentialgleichung
(3.2) unter der Nebenbedingung, daß ψ(x) quadratintegrabel ist, führt auf
Hermite-Polynome. Wir wollen hier jedoch eine algebraische Methode be-
Abb. 3.1. Potential des harmonischen Oszillators
48
3. Eindimensionale Probleme
nutzen, bei der wir versuchen, H durch das (Absolut-) Quadrat eines Operators darzustellen.
3.1.1 Algebraische Methode
Dazu definieren wir den nicht-hermiteschen Operator a durch
ωmx + ip
a= √
2ωm~
(3.4a)
ωmx − ip
a† = √
,
(3.4b)
2ωm~
und erhalten als Umkehrung
r
~
(a + a† )
x=
(3.5a)
2ωm
r
~ωm
(a − a† ) .
(3.5b)
p = −i
2
Wie man leicht aus dem Kommutator für x und p herleiten kann, gilt
[a, a† ] = 1 ,
(3.6)
während a und a† jeweils mit sich selbst kommutieren. Mit der charakteristischen Länge x0 erhält man
1
x
d
a= √
+ x0
(3.7a)
dx
2 x0
1
d
x
a† = √
− x0
.
(3.7b)
dx
2 x0
Die Relationen (3.5a,b) in (3.1) eingesetzt, ergeben für den Hamilton-Operator
H = 12 ~ω(a† a + aa† ) ,
und unter Benützung des Kommutators (3.6)
H = ~ω(a† a + 12 ) .
(3.8)
Somit ist das Problem auf die Auffindung der Eigenwerte des Besetzungszahloperators
n̂ = a† a
(3.9)
reduziert. Es sei ψν Eigenfunktion zum Eigenwert ν:
n̂ψν = νψν .
(3.10)
3.1 Der harmonische Oszillator
49
Berechnung der Eigenfunktion ψ0
Aus
ν(ψν , ψν ) = (ψν , a† aψν ) = (aψν , aψν ) ≥ 0
(3.11)
folgt
ν≥0.
Somit ist der niedrigstmögliche Eigenwert ν = 0. Um die zugehörige Eigenfunktion ψ0 zu berechnen, bemerken wir, daß auf Grund von (3.11) die Norm
von aψ0 verschwindet und deshalb
aψ0 = 0 ist, d.h.
x
d
+
ψ0 = 0 .
dx x20
Die auf 1 normierte Lösung dieser Differentialgleichung lautet
(
2 )
√
1
x
.
ψ0 (x) = ( πx0 )−1/2 exp −
2 x0
(3.12)
(3.13)
(3.14)
Berechnung der übrigen Eigenfunktionen
Aus (3.6) und (3.9) ergeben sich wegen [a† a, a† ] = a† [a, a† ] + [a† , a† ]a = a†
die wichtigen Kommutatoren
[n̂, a† ] = a†
(3.15)
[n̂, a] = −a .
(3.16)
Behauptung. a† ψν ist Eigenfunktion zum Eigenwert ν + 1.
Beweis:
n̂a† ψν = (a† n̂ + a† )ψν = (ν + 1)a† ψν .
(3.17)
Norm:
(a† ψν , a† ψν ) = (ψν , aa† ψν ) = (ψν , (a† a + 1)ψν )
= (ν + 1)(ψν , ψν ) > 0 .
Somit gilt für auf 1 normierte ψν und ψν+1
p
a† ψν = (ν + 1) ψν+1 .
Ausgehend von ψ0 erhalten wir aus (3.19)
(3.18)
(3.19)
50
3. Eindimensionale Probleme
Tabelle 3.1 Eigenzustände des harmonischen Oszillators, Eigenwerte von n̂ und H
n̂
H
Grundzustand ψ0
1. angeregter Zustand ψ1 = a† ψ0
2. angeregter Zustand ψ2 = √1 (a† )2 ψ0
0
1
2
~ω/2
3~ω/2
5~ω/2
..
.
n. angeregter Zustand ψn =
..
.
n
..
.
(n + 1/2)~ω
.
..
.
..
2
√1 (a† )n ψ0
n!
.
..
1
1
ψn = √ a† ψn−1 = √ (a† )n ψ0 ,
n
n!
(3.190 )
die in Tabelle 3.1 zusammen mit den Eigenwerten von n̂ und H angegebene unendliche Folge von Eigenzuständen. Man nennt ψ0 GrundzustandsWellenfunktion und ψn für n = 1, 2, . . . Wellenfunktion des n-ten angeregten
Zustands.
Behauptung. aψν ist Eigenfunktion mit Eigenwert ν − 1.
Beweis:
n̂aψν = (an̂ − a)ψν = (ν − 1)aψν .
(3.20)
Norm:
(aψν , aψν ) = (ψν , a† aψν ) = ν(ψν , ψν ) = ν > 0 für
(=)
Daraus folgt für ν = 0 wieder (3.12) und für ν ≥ 1:
√
aψν = ν ψν−1 .
ν > 0.
(=)
(3.21)
(3.22)
Außerdem können wir nun zeigen, daß wir in Tabelle 3.1 schon alle Zustände
gefunden haben.
Behauptung. Mit ψn , n = 0, 1, 2, . . . sind alle Eigenfunktionen gefunden.
Beweis durch Widerspruch:
Angenommen, es gäbe einen Eigenwert ν = n + α mit 0 < α < 1 und n eine
natürliche Zahl:
n̂ψν = (n + α)ψν .
3.1 Der harmonische Oszillator
51
Dann folgt aus (3.22)
n̂(an ψν ) = α(an ψν )
n̂(an+1 ψν ) = (α − 1)(an+1 ψν ) .
Da auf Grund von (3.21) die Norm der Wellenfunktion an+1 ψν existiert und
α − 1 < 0 ist, gäbe es eine Eigenfunktion von n̂ mit endlicher Norm und
negativem Eigenwert, im Widerspruch zur Positivität der Eigenwerte.
Somit sind alle stationären Zustände des harmonischen Oszillators durch
Tabelle 3.1 bzw. (3.190 ) gegeben. Die Operatoren a† (a) erhöhen (erniedrigen)
den Energieeigenwert um ~ω und werden deshalb Erzeugungs-(Vernichtungs-)
Operatoren und gelegentlich auch Leiteroperatoren genannt.
Anmerkungen: (i) Es kann jedoch nicht-quadratintegrable Eigenfunktionen mit negativem
Eigenwert geben. So ist z.B.
d2
− 2 cosh x = −cosh x ,
dx
obwohl
−
d2
=
dx2
d 2
i
dx
ein positiv-definiter Operator ist. Desgleichen ist ψ̃ = exp((x/x0 )2 /2) eine nichtnormierbare Eigenfunktion von a† (a† ψ̃ = 0) und auch von n̂ zum Eigenwert −1.
(ii) Der Grundzustand ist nicht entartet. Daraus kann man ableiten, daß auch alle
übrigen Eigenwerte von n̂ nicht entartet sind. Denn gäbe es zu einem n neben ψn eine
weitere orthonormierte Eigenfunktion ϕn , dann wäre an ϕn eine zu ψ0 orthogonale Grundzustandseigenfunktion, was einen Widerspruch darstellt.
Die Energieeigenzustände zum harmonischen Oszillator (Abb. 3.2) sind
somit
(
2 )
√
1 x
−1/2 † n
ψn = (n! π x0 )
(a ) exp −
oder
(3.23)
2 x0
(
2 )
√
1
x
x
n
−1/2
ψn = (2 n! π x0 )
exp −
Hn
2 x0
x0
(3.230 )
und die zugehörigen Energieeigenwerte lauten
En = ~ω(n + 12 )
(3.24)
mit n = 0, 1, 2, . . .. Das Spektrum der Energieeigenwerte ist diskret. Die hier
eingeführten und durch (3.23) und (3.230 ) definierten Polynome Hn werden
wir sogleich weiter untersuchen und zeigen, daß sie identisch mit den HermitePolynomen sind.
52
3. Eindimensionale Probleme
Abb. 3.2. Die Eigenfunktionen
des harmonischen Oszillators für die Quantenzahlen n = 0
p
bis 5: y = x/x0 = mω/~ x
3.1.2 Die Hermite-Polynome
Die Polynome Hn sind nach (3.23) und (3.230 ) durch
√
2
2
Hn (x) = ex /2 ( 2 a† )n e−x /2
x0 =1
n
2
2
2
2
d
= ex e−x /2 x −
ex /2 e−x
dx
definiert. Verwendet man noch die Operatoridentität
n
2
dn
d
−x2 /2
ex /2 = (−1)n n ,
e
x−
dx
dx
die aus
3.1 Der harmonische Oszillator
e−x
2
/2
x−
d
dx
ex
2
/2
=−
53
d
dx
folgt, so erhält man die übliche Darstellung für die Hermite-Polynome:
Hn (x) = (−1)n ex
2
d n −x2
e
.
dxn
(3.25)
Tabelle der ersten sechs Hermite-Polynome:
H0 (x) = 1
H1 (x) = 2x
H2 (x) = 4x2 − 2
(3.26)
H3 (x) = 8x3 − 12x
H4 (x) = 16x4 − 48x2 + 12
H5 (x) = 32x5 − 160x3 + 120x
Orthogonalitätsrelation:
Z∞
dx e−x Hn (x)Hm (x) =
2
√ n
π 2 n!δmn
(3.27)
−∞
Erzeugende Funktion:
e−t
2
+2tx
=
∞
X
1 n
t Hn (x)
n!
n=0
Differentialgleichung:
2
d
d
−
2x
+
2n
Hn (x) = 0
dx2
dx
(3.28)
(3.29)
Vollständigkeit:
∞
X
ψn (x)ψn (x0 ) = δ(x − x0 )
n=0
Hn und damit ψn hat n Knoten (einfache reelle Nullstellen).
(3.30)
54
3. Eindimensionale Probleme
3.1.3 Die Nullpunktsenergie
Klassisch ist die niedrigste Energie des harmonischen Oszillators E = 0,
quantenmechanisch ~ω/2. Da ψ0 (x) nicht V (x) allein, sondern die Summe aus
kinetischer und potentieller Energie minimalisiert, ergibt sich eine endliche
Grundzustandsenergie oder ,,Nullpunktsenergie”. Zur weiteren Illustration
berechnen wir das Unschärfeprodukt ∆x∆p. Für den Mittelwert und das
Schwankungsquadrat des Ortes finden wir
hxi = (ψn , xψn ) ∝ (ψn , (a + a† )ψn ) = 0
~
(ψn , (a2 + aa† + a† a + a†2 )ψn ) = x20 (n + 1/2) ,
2ωm
und desgleichen für den Impuls
(∆x)2 = hx2 i =
hpi = 0 ,
(∆p)2 = hp2 i =
~2
(n + 1/2) .
x20
Somit ergibt sich für das Unschärfeprodukt
∆x∆p = (n + 1/2)~ .
(3.31)
Dies ist für den Grundzustand minimal. Die Grundzustandswellenfunktion
ist nicht etwa auf x = 0 – das Minimum des Potentials – konzentriert, sondern hat die Ausdehnung x0 und eine endliche zugehörige Ortsunschärfe (=
Schwankung). Man bezeichnet diesen für die Quantentheorie charakteristischen Sachverhalt als ,,Nullpunktsschwankung”. Wir wollen noch eine Ungleichung für die Nullpunktsenergie ohne explizite Berechnung der Wellenfunktion, nur auf Grund der Unschärferelation
∆x∆p ≥
~
2
(3.32)
herleiten. Da aus Symmetriegründen für den Grundzustand hpi = hxi = 0
sein muß (siehe Abschn. 3.6), folgt
hp2 ihx2 i ≥
~2
,
4
und somit die folgende Ungleichung für die Energie:
E = hHi =
hp2 i 1
hp2 i mω 2 ~2 1
+ mω 2 hx2 i ≥
+
.
2m
2
2m
2 4 hp2 i
Die Ableitung nach hp2 i liefert als Bedingung für das Minimum
1
mω 2 ~2
1
−
=0
2m
8
(hp2 imin )2
hp2 imin =
m~ω
.
2
und somit
3.1 Der harmonische Oszillator
55
Für die Energie gilt dann
E≥
mω 2 ~2 2
~ω
m~ω
+
=
.
2m . 2
8
m~ω
2
Die Nullpunktsenergie ist der kleinste Energiewert, der mit der Unschärferelation vereinbar ist.
Anmerkung: Vergleich mit dem klassischen Oszillator. Für die klassische Bewegung gilt
x = q0 sin ωt
E=
1
mω2 q02
2
(3.33)
.
(3.34)
Wir definieren eine klassische ,,Aufenthaltswahrscheinlichkeit”
Wklass (x)dx =
dt
,
T
wobei dt die Aufenthaltsdauer in dx und T = 2π/ω sein sollen. Aus (3.33) folgt
q
dx = q0 ω cos ωt dt = q0 ω 1 − (x/q0 )2 dt , und somit
Wklass =
2πq0
p
1
1 − (x/q0 )2
.
(3.35)
Beispiel:
Der 1. angeregte Zustand besitzt die Energie E1 = (3/2)~ω. Mit (3.34) folgt (Abb. 3.3)
r
√
3~ω
= 3 x0 .
q0 =
mω2
Abb. 3.3. Vergleich der quantenmechanischen (—) mit der ,,klassischen” (- - -) Aufenthaltswahrscheinlichkeit für (a) Energie E1 und (b) E10
92
3. Eindimensionale Probleme
Aufgaben zu Kapitel 3
3.1 Die Hermite-Polynome Hn (x) sind in (3.25) definiert.
2
(a) Zeigen Sie, daß e−t +2tx erzeugende Funktion der Hermite-Polynome ist, d.h.
e−t
2
+2tx
=
∞
X
tn
Hn (x) .
n!
n=0
(∗)
(b) Zeigen Sie durch Ableiten von (∗) die Gültigkeit der Rekursionsrelationen
Hn0 (x) = 2n Hn−1 (x)
und
Hn+1 (x) = 2x Hn (x) − 2n Hn−1 (x) .
(c) Beweisen Sie die Vollständigkeitsrelation (3.30).
Anleitung: Drücken Sie Hn (x) und Hn (x0 ) durch (3.25) aus und stellen Sie die
Gauß-Funktionen durch ihre Fourier-Transformierte dar.
(d) Zeigen Sie, daß die Hermite-Polynome und damit die ψn n Knoten (einfache
reelle Nullstellen) im Endlichen besitzen.
Anleitung: Induktionsschluß, Satz von Rolle.
3.2 (a) Zeigen Sie, daß die kohärenten Zustände in der Form (3.3700 ) geschrieben
werden können.
Anleitung: Verwenden Sie (2.47).
(b) Weisen Sie nach, daß
1
2
(ϕα , ϕβ ) = e− 2 (|α|
+|β|2 )+α∗ β
gilt.
(c) Beweisen Sie die Relation
Z 2
d α
ϕα (x)ϕ∗α (x0 ) = δ(x − x0 ) ,
π
wobei d2 α ≡ d(Re α) d(Im α) ist.
3.3 Der klassische Grenzfall des harmonischen Oszillators (s. Ende von Abschn. 3.1).
Betrachten Sie den kohärenten Zustand ϕα (x) für |α| 1.
(a) Zeigen Sie unter Benutzung der Stirling-Formel,
√
für n 1 ,
n! ≈ 2πn nn e−n
daß der Betrag der Amplitude
αn
√
n!
für
n0 = |α|2
maximal ist.
(b) Zeigen Sie, daß der Mittelwert hn̂i des Operators n̂ im Zustand ϕα gleich n0
ist.
.
(c) Berechnen Sie ∆n
hn̂i
(d) Zeigen Sie, daß der Mittelwert der Energie in diesem Grenzfall
Aufgaben zu Kapitel 3
93
(ϕα , Hϕα ) = ~ω|α|2
ist. Vergleichen Sie dieses Ergebnis mit dem klassischen Resultat.
3.4 In diesem Beispiel werden nichtnormierte und deshalb unphysikalische Lösungen
des harmonischen
Oszillators diskutiert.
2
2
(a) Ist ex /2x0 Eigenfunktion des Operators n̂ = a† a ?
(b) Können Sie eine divergente Eigenfunktion von n̂ zum Eigenwert 0 angeben?
(c) Wieso treten diese unphysikalischen Lösungen bei der algebraischen Methode
nicht auf?
3.5 Der heutige Stand der Halbleitertechnik gestattet die Herstellung von Bauelementen, in denen sich die Elektronen in zwei Dimensionen (der (y, z)-Ebene etwa)
frei bewegen können, während in der dritten Dimension (x-Achse) durch geeignete
Materialschichtungen (man beherrscht sogar einatomige Monolagen) sehr schmale,
hohe Potentialtöpfe erreicht werden können, die zu einer scharfen Quantisierung
der Bewegung in dieser Richtung führen.
In dieser Aufgabe ist ein einzelner, unendlich hoher Potentialtopf (das gibt es
fast) zu behandeln. Denken Sie sich die freie Bewegung in der (y, z)-Ebene absepariert und lösen Sie folgende Teilfragen:
(a) Bestimmen Sie die Eigenfunktionen und Energieeigenwerte für die Bewegung
im unendlich hohen Potentialkasten
(
0
für x ∈ (−a, a)
V (x) =
∞ sonst .
(b) Zeigen Sie, daß das System der Eigenfunktionen vollständig ist.
(c) Bestimmen Sie die Impulsverteilung für ein Teilchen, das sich im n-ten Energieeigenzustand befindet.
3.6 Lösen Sie die stationäre Schrödinger-Gleichung für das Potential
x
.
V (x) = −~2 / ma2 cosh2
a
Anleitung: Führen Sie y =
x
a
ein, machen Sie den Ansatz
ψ(y) = eiky ϕ(y)
und substituieren Sie z = tanh y. Die resultierende Gleichung kann durch einen
Potenzreihenansatz in Verbindung mit einer Abbruchbedingung elementar gelöst
werden. Diskutieren Sie die auftretenden Lösungen.
3.7 (a) Berechnen Sie den Bindungszustand und die Streuzustände für das eindimensionale Potential
V (x) = −λδ(x)
mit λ > 0.
(b) Beweisen Sie die Vollständigkeitsrelation für diese Zustände.
3.8 Im Sinne der Einleitung zur Aufgabe 3.5 lassen sich auch sogenannte “Doppelheterostrukturen” herstellen. Betrachten Sie als einfachste Realisierung einen
unendlich hohen Potentialtopf, in dem sich eine δ-Barriere befindet. (Siehe schematische Abbildung.)
(a) Bestimmen Sie die normierten Eigenfunktionen und geben Sie eine Formel für
die Energieeigenwerte an.