Semiempirische Methoden

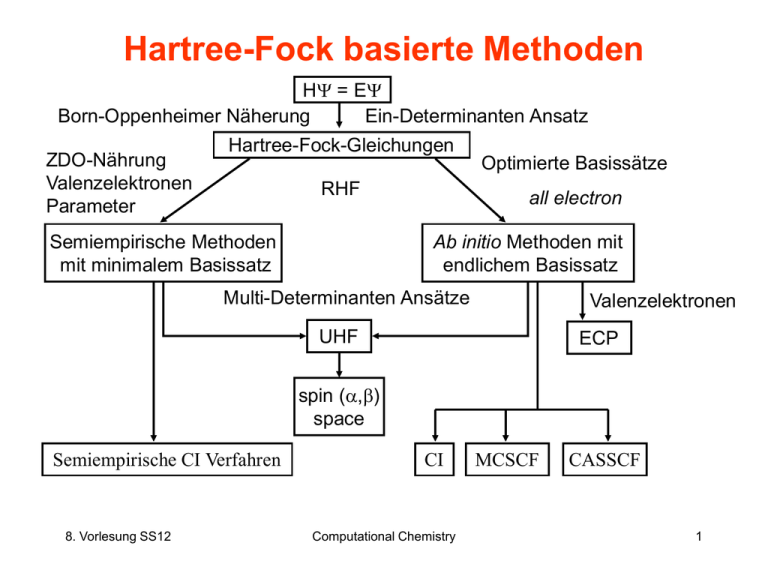
Hartree-Fock basierte Methoden
HY = EY
Born-Oppenheimer Näherung
Ein-Determinanten Ansatz
ZDO-Nährung
Valenzelektronen
Parameter
Hartree-Fock-Gleichungen
RHF
Semiempirische Methoden
mit minimalem Basissatz
Optimierte Basissätze
all electron
Ab initio Methoden mit
endlichem Basissatz
Multi-Determinanten Ansätze
Valenzelektronen
UHF
ECP
spin (a,b)
space
Semiempirische CI Verfahren
8. Vorlesung SS12
CI
Computational Chemistry
MCSCF
CASSCF
1
Semiempirische Methoden (I)
Im Gegensatz zu ab initio Rechnungen wurden die
semiemprischen Methoden zum Teil auch an experimentellen
Daten kalibriert:
• Bildungswärmen (DHfo)
• Molekülgeometrien (Bindungslängen, Winkel)
• Dipolmomente (m)
• Ionisationspotentiale (IP)
Dadurch sind die Ergebnisse von semiempirische Methoden
bei diesen Eigenschaften oft denen von ab initio Rechnungen
auf niedrigem Niveau (mit vergleichbartem Rechenaufwand)
überlegen.
8. Vorlesung SS12
Computational Chemistry
2
Semiempirische Methoden (II)
Das Problem von ab initio Rechnungen ist die N4 Abhängigkeit
von der Anzahl der Zwei-Elektronen Integrale.
Lösungsansatz und Näherungen:
1. Nur Valenzelektronen werden betrachtet, Rumpfelektronen
werden mittels der effektiven Kernladung beschrieben die ein
effektives Potential bilden (frozen core).
2. Minimaler Basissatz wird verwendet (ein s und drei p-Orbitale
pro Atom), aber dafür exakte STOs die orthogonal zueinander
sind.
3. Zero Differential Overlap (ZDO) Näherung
8. Vorlesung SS12
Computational Chemistry
3
ZDO Näherung (I)
Zero Differential Overlap (ZDO) Näherung bedeutet:
Alle Produkte von Basisfunktionen an verschiedenen Kernen, die
sich auf dasselbe Elektron i beziehen, werden auf Null gesetzt
m A  B  0

 m   d   0
d.h. Es findet keine Überlappung in einem beliebigen Volumenelement d statt .
Aber: Das Integral über die Basisfunktionen ist nicht Null!
(Beschreibt die chemische Bindung zwischen Atomen)
Anmerkung zur Notation:
mA : Atomorbital an Atom A
Die semiempirischen Atomorbitale m, , ,  entsprechen den
ab initio Basisfunktionen a, b, , 
8. Vorlesung SS12
Computational Chemistry
4
ZDO Näherung (II)
Folgen der ZDO-Näherung:
1. Die Überlappungsmatrix S reduziert sich zur Einheitsmatrix E
S m   m
FC  SCE

FC  CE
2. Integrale an 3 und 4 Zentren werden vernachlässigt (haben
den zahlenmäßig größten Anteil an den Zwei-Zentren
Integralen)
8. Vorlesung SS12
Computational Chemistry
5
Semiempirische Methoden (III)
Als Näherungen für Ein- und Zwei-Elektronenintegrale erhält man
ausgehend vom der ab initio Formel
a F  b  a h  b 
   c c   a  
occ.MO
AO AO
j

j
j
g  b   a  g   b


die analogen semiempirischen Elemente der Fockmatrix
AO AO
Fm  h m 
  D   m

|   
1
2
 m
| 


mit den Ein-Elektronen Integralen
h m  m h 
K
und dem Ein-Elektronen Operator
hi     
1
2
2
i
a
8. Vorlesung SS12
Computational Chemistry
Za
R a  ri
6
Semiempirische Methoden (IV)
N/2
den Elementen der Dichtematrix
D   2  c  i  c  i
i 1
den Zwei-Elektronenintegralen
m 
 m 1   2  g 12  1    2 
dem Zwei-Elektronen Operators
g 12 
1
r1  r2
Die semiempirischen Methoden unterscheiden sich in der
Art und Weise wie die Ein- und Zwei-Elektronenintegrale
konkret berechnet, bzw. parametrisiert werden.
Damit reduziert sich der Rechenaufwand hauptsächlich auf
die Ein- und Zwei-Elektronen-Operatoren.
Problem: In wie weit läßt sich die gegenseitige Überlappung
der Orbitale vernachläßigen? → differential overlap
8. Vorlesung SS12
Computational Chemistry
7
CNDO Complete Neglect of Differential
Overlap (I)
Pople, Santry & Segal J. Chem. Phys. 43 (1965) S129-135
 Drastische Reduzierung der Mehrzentrenintegrale
Verwendet folgende Parameter:
• Core Hamiltonian Umm aus Ionisierungsenergien
• Elektronrepulsionsintegrale AB
• Resonanzintegral bAB aus ab initio Rechnungen an
zweiatomigen Molekülen
Zu berechnen sind:
• Überlappungsintegrale Sm
• Elektron-Kern Wechselwirkungsterme VAB
8. Vorlesung SS12
Computational Chemistry
8
CNDO Complete Neglect of Differential
Overlap (II)
Mit CNDO berechenbare Größen:
+ Bildungswärmen
+ Ionisierungspotentiale
+/– Dipolmomente (mit Einschränkungen)
Nachteile von CNDO bzw. CNDO/1:
– Vernachlässigung der Einzentrenaustauschintegrale führt
zu schlechten optimierten Molekülgeometrien
– Zwei neutrale Atome die mehrere Ångstrom entfernt sind
ziehen sich an
– Die resultierenden Bindungslängen sind zu kurz
– Die Bindungsdissoziationsenergien sind zu hoch
8. Vorlesung SS12
Computational Chemistry
9
CNDO/2 und CNDO/S (I)
Abhilfe schaffte die CNDO/2 Methode (Pople and Segal
J. Chem. Phys. 44 (1966) 3289-3296) indem dem der ElektronKern-Wechselwirkungsterm VAB modifiziert wurde
Zur Berechnung von optischen Spektren wurde darüber
hinaus die CNDO/S Methode speziell parametrisiert
(Del Bene & Jáffe J. Chem. Phys. 48 (1968) 1807).
8. Vorlesung SS12
Computational Chemistry
10
CNDO/S (II)
Beispiel: UV-Übergänge in Benzol (Energien in eV)
Übergang
CNDO/S
exptl.
nach
3B
1u
3.7
3.89
1B
2u
4.7
4.89
1B
1u
5.2
6.18
1E
1u
6.9
6.95
E


0


8. Vorlesung SS12

{
} 1E
1u
1B
1u
1B
2u
3B
1u

1
A 1g
Computational Chemistry
11
INDO Intermediate Neglect of Differential
Overlap (I)
Pople, Beveridge & Dobosh J. Chem. Phys. 47 (1967) 20261033
 Berücksichtigung der Überlappung von Basisfunktionen am
selben Atom
Dadurch wird nun die Singulett-Triplett-Aufspaltung
berücksichtigt (T-Zustand ist v.a. an einem Atom energetisch
günstiger)
T rip le tt
S in g u le tt
Folge: Spindichten (EPR) werden besser als mit CNDO
erhalten
8. Vorlesung SS12
Computational Chemistry
12
INDO Intermediate Neglect of Differential
Overlap (II)
Die verwendeten Ein-Zentren-Zwei-Elektronenintegrale können
als sog. Slater-Condon-Parameter aus Atomspektren
entnommen werden. Bsp:
ss ss  ss pp  
AA
F
o
sp x sp x  sp y sp y  sp z sp z 
1
2
G
1
px px px px  py py py py  pz pz pz pz  F 
o
8. Vorlesung SS12
Computational Chemistry
4
25
F
2
13
INDO Intermediate Neglect of Differential
Overlap (III)
Mit INDO berechenbare Größen:
+ Ionisierungspotentiale
+ Dipolmomente
+ Spindichten und Hyperfeinkopplungskonstanten (EPR)
Nachteile von INDO:
– schlechte optimierte Molekülgeometrien
Zur Berechnung von optischen Spektren wurde außerdem
eine spezielle INDO/S Parametrisierung entwickelt. (Ridley
& Zerner Theor. Chim. Acta 32 (1973) 111).
Für die Berechnung von EPR Spektren bei großen
Molekülen ist INDO immer noch von Bedeutung
8. Vorlesung SS12
Computational Chemistry
14
Weitere INDO basierte Methoden
MINDO/3
Konsequente Kalibrierung an experimentellen Daten. Bis dato
wurde versucht ab initio Rechnungen zu reproduzieren.
SINDO1
Zur Berechnung von Verbindungen mit Übergangsmetallen.
ZINDO M. Zerner et al.
Zur Berechnung von von Spektren bei Übergangsmetallen.
8. Vorlesung SS12
Computational Chemistry
15
NDDO Neglect of Diatomic Differential
Overlap (I)
Theorie-Basis für alle modernen semiempirischen Verfahren
 Vernachlässigt wird nur die Überlappung von Atomorbitalen,
die auf unterschiedlichen Atomen A und B sind
Gegenüber INDO sind damit für jedes Paar von NichtWasserstoffsatomen A und B, 100 mal mehr Integrale zu
berechnen oder zu parametrisieren.
Prinzipielle Vorteile gegenüber CNDO und INDO:
+ verwendete Orbitale haben s oder p Charakteristik
+ dadurch wird die Bindungsrichtung besser beschrieben
8. Vorlesung SS12
Computational Chemistry
16
MNDO Modfied Neglect of Diatomic
Overlap (I)
Dewar, Thiel et al. J. Am. Chem. Soc. 99 (1977) 4899-4917
Im Gegensatz zu INDO-basierten Ansätzen treten hier nur
noch elementspezifische Parameter auf.
Verwendet werden folgende Parameter (pro Element):
• Einelektronenterme Us, Up, bs, bp
• zwei getrennte Orbitalexponenten für die s und p-Orbitale
• ein Parameter a für die Kern-Kern Abstoßung
• 5 Einzentren-Zweielektronenintegrale die den Coulomb,
bzw. den Austauschintegralen entsprechen
8. Vorlesung SS12
Computational Chemistry
17
MNDO Modfied Neglect of Diatomic
Overlap (II)
Vorteile von MNDO:
+ Bildungswärmen
+ Ionisierungspotentiale
+ große Anzahl parametrisierter Elemente
+ Optimierung zu realistischen Molekülgeometrien
Nachteile von MNDO:
– gegenseitige Abstoßung ungeladener Moleküle
– deswegen lassen sich keine H-Brücken darstellen
– zu niedrige Rotationsbarrieren (um Einfachbindungen)
8. Vorlesung SS12
Computational Chemistry
18
AM1 Austin Model 1 (I)
Dewar, Stewart et al. J. Am. Chem. Soc. 107 (1985) 3902
Modifizierung der MNDO Kern-Kern-Abstoßungsfunktion durch
Hinzufügen von 2-4 Gaußfunktionen. → Fit-Funktionen
Differenz der Kern-Kern-Abstoßungsterme zwischen AM1 und
MNDO. Entnommen aus A. Leach, Molecular Modelling
8. Vorlesung SS12
Computational Chemistry
19
AM1 Austin Model 1 (II)
Vorteile gegenüber MNDO:
+ bessere Molekülgeometrien v.a. bei hypervalenten
Elementen (P, S)
+ H-Brücken (aber mit der Tendenz zur Gabelung)
+ Aktivierungsenergien bei chemischen Reaktionen
+ Rotationsbarrieren
Schwächen von AM1:
– hypervalente Elementen allgemein, da keine d-Orbitale
– Verbindungen mit freien Elektronenpaaren
– NO2-Verbindungen
– H-Brücken oft gegabelt anstelle von linear
8. Vorlesung SS12
Computational Chemistry
20
PM3 Parameterized Method 3 (I)
J. J. P. Stewart J. Comput. Chem. 10 (1989) 209
Analog zu AM1, aber jeweils 2 Gaußfunktionen
Im Gegensatz zu den bisherigen Methoden erfolgte die
Parametrisierung stärker durch statistisches Kalkül.
Vorteile gegenüber AM1:
+ bessere Molekülgeometrien bei C, H, P und S
+ NO2-Verbindungen besser
+ H-Brückengeometrien oft besser
8. Vorlesung SS12
Computational Chemistry
21
PM3 Parameterized Method 3 (II)
Nachteile gegenüber AM1:
– Alle übrigen N-haltigen Verbindungen schlechter
– höhere Atomladungen führen zu polarerem Charakter der
Moleküle (höheres Dipolmoment)
– zu niedrige Rotationsbarrieren
– Nicht alle parametrisierten Elemente (Mg, Al, Zn) liefern
zuverläßige Ergebnisse für alle Substanzklassen
→ Re-Parametrisierungsansätze auf NDDO-Basis
8. Vorlesung SS12
Computational Chemistry
22
Neue Methoden seit 1995 (I)
MNDO/d
Thiel und Voityuk J. Phys. Chem. 100 (1996) 616
Erweitert die MNDO-Methode um d-Obitale und ist
“kompatibel” mit den bereits für MNDO parametrisierten
Atomen
PM3(tm)
d-Orbitale für Elemente der Übergangsreihen (Fe, Cu,...)
SAM1 Semi ab initio Method 1
A. Holder und M. Dewar
Bestimmte Integrale werden konsequent berechnet, deshalb
auch für Übergangsmetalle (Cu, Fe) anwendbar
8. Vorlesung SS12
Computational Chemistry
23
Neue Methoden seit 1995 (II)
OM1 und OM2
W. Weber und W. Thiel, Theor. Chem. Acc. 103 (2000) 495
Orthogonalisierungskorrekturen für NDDO
v.a. elektronische Übergänge (Spektren) besser
PM5
J.P.P. Stewart (2001)
NNDO mit zusätzlichem Atompaarterm für die Kern-KernAbstoßung wie in MINDO/3
v.a. Bildungswärmen besser
PM6
J.P.P. Stewart (2007)
Fokus auf Wasserstoffbrückenbindungen
8. Vorlesung SS12
Computational Chemistry
24
Neue Methoden seit 1995 (III)
AM1/d und AM1*
Erweitert die AM1-Methode um d-Obitale und ist
“kompatibel” mit den anderen für AM1 parametrisierten
Atomen.
AM1* Winget, Horn et al. J.Mol.Model. (2003) 408.
Reparameteriesierungen
RM1
NNDO Ansatz von AM1 neu parameterisiert
Simas, Stewart et al. J.Comput.Chem. 17 (2006) 1101.
8. Vorlesung SS12
Computational Chemistry
25
Bildungswärmen
Berechnung der Bildungswärmen von Verbindungen bei 25° C
Atome
D H f o ( Molekül )  E elec ( Molekül ) 
E
Atome
elec
( Atome ) 
 DH
f
o
( Atome )
Atomisierungs Bildungswärmen
energien
der Elemente
Experimentell bekannt
Berechnet werden muß also die elektronische Energie
O
H
O
A to m is ie ru n g
H
8. Vorlesung SS12
H
E elec (M olekül)
H
Computational Chemistry
O
H
H
26
Vergleich der Methoden
Berechnung der Bildungswärmen von Verbindungen bei 25° C
Durchschnittlicher absoluter Fehler (in kcal/mol)
Anzahl Verbindungen
Methode
(C, H, N, O, sowie)
MNDO
AM1
PM3
Al (29)
22.1
10.5
16.4
4.9
Si (84)
12.0
8.5
6.0
6.3
P (43)
38.7
14.5
17.1
7.6
S (99)
48.4
10.3
7.5
5.6
Cl (85)
39.4
29.1
10.4
3.9
Br (51)
16.2
15.2
8.1
3.4
I (42)
25.4
21.7
13.4
4.0
Zn (18)
21.0
16.9
14.7
4.9
Hg (37)
13.7
9.0
7.7
2.2
Mg (48)
9.3
15.4
12.0
9.3
8. Vorlesung SS12
Computational Chemistry
MNDO/d
27
Open Source Programme
MOPAC 7.1 (und MOPAC2007) J.J.P. Stewart
http://openmopac.net/
GHEMICAL
http://www.bioinformatics.org/ghemical/ghemical/index.html
8. Vorlesung SS12
Computational Chemistry
28
Zusammenfassung Semiempirik
Durch Weglassen bestimmter Mehrzentrenintegrale wird der
Rechenaufwand im Vergleich zu ab initio QM drastisch
verringert.
Das Ausmaß der jeweiligen ZDO-Näherung bestimmt auch die
„Qualität“ der Methode.
Aufgrund der Parameterisierung an experimentellen Daten
lassen sich entsprechende Meßwerte (z.B. Bildungsenergie)
mit geringem Rechenaufwand vorhersagen.
Als Basis-Funktionen werden Slater-Typ Orbitale verwendet.
Neuere Methoden verwenden nun auch d-Orbitale neben sund p-Orbitalen und teilweise zusätzliche Integrale.
Die Stärken und Schwächen der am häufigsten verwendeten
Methoden (MNDO, AM1 und PM3) sind gut bekannt.
8. Vorlesung SS12
Computational Chemistry
29
Solvatationsmodelle
Wozu ?
Alle biologisch relevanten Reaktionen finden in
wässriger Lösung statt
Vorhersage von molekularen Eigenschaften:
• Solvatationsenergien
• Bindungsaffinitäten in Enzym-Ligand Systemen
• Protonierungszustände von Residuen und Liganden, pKa
8. Vorlesung SS12
Computational Chemistry
30
Was ist Solvatation ?
g a s / va p o u r
s u b lim a tio n
s o lv a tio n
s o lid
s o lve n t
8. Vorlesung SS12
Computational Chemistry
31
Aminosäuren in Wasser (1)
R
R
O
H 2O
H
N
H
O
H
O
+
N
H
H
H
O
Einzelne Aminosäuren dissoziieren in Wasser:
Carbonsäuren als schwache Säuren zu Carboxylaten
Amine als schwache Basen bilden Ammoniumgruppen
Auch die Seitenketten können ihren Protonierungszustand
ändern (titrierbare Gruppen eines Proteins)
8. Vorlesung SS12
Computational Chemistry
32
Aminosäuren in Wasser (2)
Wie verhält sich die Carbonsäuregruppe der Seitenkette von
Asp oder Glu bei unterschiedlichem pH ?
H 3 C-CO O H + H 2 O
H 3 C-CO O - + H 3 O +
HAc
A c-
Die Umsetzung einer Säure mit einer Base liefert eine
Titrationskurve
HAc + NaO H
Na + Ac - + H 2 O
0
pH
2
4
pKa
6
8
10
12
14
pH
1 0 -1
Ac
0
-
1 0 -2
1 0 -3
1 0 -4
4 .7
1 0 -5
1 0 -6
14
H Ac
1 0 -7
[N a O H ]
OH-
H 3O +
K o n ze n tra tio n m o l/l
8. Vorlesung SS12
Computational Chemistry
33
Aminosäuren in Wasser (3)
typische pKa-Werte von Aminosäurenseitenketten
(dargestellt in ihrer protonierten Form als Säure)
A sp
O
3 .9
C H2
OH
O
G lu
C H2
4 .1
C H2
OH
H
+
L ys
C H2 C H2 C H2
C H2 N
H
1 0 .8
H
H
A rg
N
+
C H2 C H2 N
H
C
1 2 .5
N
H
H
H
H
+
H is
N
C H2
6 .0 4
N
P ro to n ie ru n g ka n n sich
ä n d e rn
H
8. Vorlesung SS12
Computational Chemistry
34
Aminosäuren in Wasser (4)
typische pKa-Werte von Aminosäurenseitenketten
(dargestellt in ihrer protonierten Form als Säure)
Ser
C H2 O H
13
Thr
CH
13
OH
C H3
T yr
C ys
C H2
C H2 S H
OH
1 0 .1
8 .3
O xid a tio n zu
D isu lfid b rü cke n
Diese pKa-Werte wurden für einzelne Aminosäuren in Lösung
bestimmt (bulk properties). Im Protein kann sich der Wert je
nach Umgebung ändern.
8. Vorlesung SS12
Computational Chemistry
35
Komplexbildung in Lösung (1)
DGgas
Gas
L
DGsol(L)
Lösung
+
E
L+ELE
DGsol(E)
L
+
L
E
Verdrängung von
Wassermolekülen
aus der Bindungstasche ist
vorwiegend
entropisch
DGsol(LE)
E
DGass
L
E
DGass  DGgas(L+ELE) + DGsol(LE) – DGsol(L) – DGsol(E)
8. Vorlesung SS12
Computational Chemistry
36
Komplexbildung in Lösung (2)
L + E  LE
Massenwirkungsgesetz: DG  RT ln Kon
 RT ln ( [LE] / [L] [E] )
Für Wirkstoffe sollte die Bindungskonstante Kon im nanomolaren
Bereich sein
milli
micro nano
m
m
n
10-3
10-6
10-9
8. Vorlesung SS12
pico femto
p
f
10-12 10-15
Computational Chemistry
37
Vorgänge bei der Solvatation
H
O
H
H
H
H
H
H
O
H
H
H
H
H
H
O
H
H
H
H
H
continuum
DGestat + DGvdw
co n tin u u m
co n tin u u m
DGcav
DGsolv  DGcav + DGestat + DGvdw
8. Vorlesung SS12
Computational Chemistry
38
Berechnung der Terme (1)
DGsolv  DGcav + DGestat + DGvdw
Cavity energy DGcav Hohlraumbildungsenergie
• Ausformen einer Kavität gegen den Druck
des Solvens
• Reorganisation der Solvensmoleküle
proportional zu der Wahrscheinlichkeit einen
entsprechenden Hohlraum zwischen den
Lösungsmittelmolekülen zu finden
R. A. Pierotti Chem.Rev. 76 (1976) 717.
8. Vorlesung SS12
Computational Chemistry
39
Berechnung der Terme (2)
DGsolv  DGcav + DGestat + DGvdw
van der Waals Energie DGvdw
• schwache Wechselwirkungen durch
fluktuierende elektrische Momente
(Dispersion)
• u.a. abhängig von der Polarisierbarkeit
Von Bedeutung falls das Lösungsmittel eine kleine
Dielektrizitätskonstante hat (e < 10) und das gelöste
Molekül keine Ladung und kein permanentes
Dipolmoment hat. Dann ist DGestat relativ klein.
8. Vorlesung SS12
Computational Chemistry
40
Berechnung der Terme (3)
DGsolv  DGcav + DGestat + DGvdw
Elektrostatische Energie DGestat
• starke Wechselwirkung, deshalb
dominierender Term
DGsolv 1-10 kcal/mol für neutrale Moleküle
ca. 100 kcal/mol für Ionen (Na+, Ca2+,...)
In der Regel sind DGestat und DGcav
größenordnungsmäßig gleich
8. Vorlesung SS12
Computational Chemistry
41
Solvatationsmodelle (1)
Solvens als strukturloses
Kontinuum
Explizite
Lösungsmittelmoleküle
(Supermolekülansatz)
Erste Lösungmittelhülle explizit,
weiteres Lösungsmittel als Kontinuum
Vorteil: H-Brücken mit dem Lösungsmittel werden
besser erfaßt als im reinen Kontiuumsansatz
Alternative: An entsprechenden Stellen plaziert man
explitize Wassermoleküle
8. Vorlesung SS12
Computational Chemistry
42
Solvatationsmodelle (2)
Born (1920) Ladung/Ion in einer kugelförmigen cavity
DGestat = Arbeit um ein Ion
aus dem Vakuum in die
Lösung zu bringen
+
2
D G estat
q 
1

1



2a 
e 
q : Ladung in e
a : Radius
e : Dielektrizitätskonstante (DK)
Wasser = 80 Vakuum = 1
Protein = 2-20
8. Vorlesung SS12
Computational Chemistry
43
Solvatationsmodelle (3)
Onsager/Kirkwood (1930) Dipol in einer cavity
Das Dipolmoment m des gelösten Moleküls
induziert ein Dipolmoment im Lösungsmittel,
das seinerseits ein elektrisches Feld  in der
cavity erzeugt, das sog. Reaktionsfeld
 RF 
( 2 e  1)
( 2 e  1) a
D G estat  
3
m
Unter Berücksichtigung der Ladungsverteilung in der cavity erhält man
 RF m
2
Im Falle von geladenen Molekülen kommt noch ein entsprechender
Born-Term hinzu.
8. Vorlesung SS12
Computational Chemistry
44
Solvatationsmodelle (4)
Dieser Reaktionsfeldansatz kann in quantenmechanischen Methoden
verwendet werden und zwar als Störung des ursprünglichen
Hamiltonians
Hˆ tot  Hˆ o  Hˆ RF
wobei
T
Hˆ RF   mˆ
2 (e  1)
( 2 e  1) a
3
 mˆ 
Schwachpunkt ist die kugel- oder ellipsoide Form der cavity, die für
die meisten Moleküle unzutreffend ist.
• Für willkürliche Formen benutzt man deshalb Punktladungen an
der Cavityoberfläche die aus der Wellenfunktion (QM) oder
Atomladungen (Kraftfelder) abgeleitet werden.
• Point Charge Method (PCM)
8. Vorlesung SS12
Computational Chemistry
45
Solvatationsmodelle (5)
Variante der point charge method:
In COSMO (A. Klamt) ist die cavity in einem Leiter mit unendlich
hohem e untergebracht (metallischer Leiter) und die Ergebnisse
werden auf realistische e skaliert.
Verbesserung: COSMO-RS (real solvent)
Beschreibt die Wechselwirkung in einer Flüssigkeit als lokale,
paarweise Interaktion der Moleküloberflächen
Vorteile: H-Brücken werden besser als
in Kontinuumsansätzen beschrieben
Anwendbar auf Mischungen von
Flüssigkeiten
http://www.cosmologic.de/theory_background.html
8. Vorlesung SS12
Computational Chemistry
46
Generalized Born Equation (1)
Kontinuummethode für Kraftfelder, N Atome als Partikel mit Radius ai
und Ladung qi
Die gesammte freie elektrostatische Energie ist dann die Summe
aus Coulomb und freier Born Energie
N
D G estat 
N

i 1 j  i  1
qi q j
e rij
2
N
q
1


 1 2 1    i
e  i 1 a i

In den üblichen Programmen z.B. AMSOL (Cramer & Truhlar) oder
OPLS, wird folgende Formel verwendet:
D G estat
8. Vorlesung SS12
N
1


  1 2 1  
e  i 1

N
qi q j
 f r
j 1
ij
, a ij 
Computational Chemistry
47
Generalized Born Equation (2)
Die Funktion f(rij, aij) berücksichtigt dabei, ob die Ladungen qi und
qj nahe bei einander sind (→ Onsager Theorie) oder weit entfernt
sind r >>ai wobei die Energie dann die Summe aus Coulomb und
Born Term ist (Still).
f rij , a ij  
2
rij  a ij e
2
2
D
mit a ij 
a i a j und D 
rij
( 2 a ij )
2
Aufwendig ist die Bestimmung des effektiven Born Radius ai für
jede Atomladung im System während der Rechnung. U.a. wird
dazu die solvent accessible area (SASA) der Atome benötigt.
S
S
8. Vorlesung SS12
Computational Chemistry
48
Langevin Dipol Modell
Warshel & Levitt (1976)
Auf einem dreidimensionalen Gitter
werden die Lösungsmittelmoleküle
als Dipole mi dargestellt, wobei Eio
das Feld aufgrund des Moleküls
allein ist.
D G sol  
1
2

m i Ei
o
i
8. Vorlesung SS12
Computational Chemistry
49
Poisson-Boltzmann Gleichung (1)
Geeignet für große Moleküle (Proteine, DNA-Stränge)
e= 8 0
e= 4
Die Poisson Gl. stellt einen Zusammenhang
zwischen dem Potential  und der
Ladungsdichte r in einem Medium mit
homogenem e dar
  (r )  
2
4r ( r )
e
Im Falle von Punktladungen in einem konstanten Dielektrikum geht
die Poisson Gl. in das Coulombsche Gesetz über. Variiert man nun
e mit der Position r dann ist
 e ( r )   ( r )   4r ( r )
8. Vorlesung SS12
Computational Chemistry
50
Poisson-Boltzmann Gleichung (2)
Kommen nun noch bewegliche Ionen in der Lösung vor, so
werden diese mittels einer Boltzmann-Verteilung beschrieben
  V (r ) 

n ( r )  N exp 

k
T
b


Zusammen erhält man die Poisson-Boltzmann Gleichung
 e ( r )   ( r )  k sinh  ( r )    4r ( r )
'
k‘ erhält man über die inverse Debye-Hückel-Länge k mit
I als der ionischen Stärke der Lösung
k
2

k
'2
e
8 N A e I
2

8. Vorlesung SS12
1000 e k b T
I 
1
2
c
i
z
2
i
i
Computational Chemistry
ci Konzentration
zi Ladungszahl
51
Poisson-Boltzmann Gleichung (3)
Der sinh läßt sich alternativ als Taylor-Reihe darstellen
2
4


 (r )
 (r )
 e ( r )   ( r )  k  ( r ) 1 

     4r ( r )
6
120


'
In der linearisierten PB-Gl. wird nur der erste Term verwendet
 e ( r )   ( r )  k  ( r )   4r ( r )
'
Analytisch lassen sich nur sehr einfache geometrische
Formen der Moleküle lösen:
• Proteine als Kugeln oder Ellipsen (Tanford-Kirkwood)
• DNA als Zylinder
• Membranen als Ebenen (Gouy-Chapman)
8. Vorlesung SS12
Computational Chemistry
52
Poisson-Boltzmann Gleichung (4)
Als numerische Lösung kommt v.a. die finite difference Methode
zum Einsatz (Warwick & Watson 1982) z.B. verwendet im
Programm DelPhi (Barry Honig)
Dazu werden elektrostatisches Potential ,
Ladungsdichte r, DK e und ionische Stärke I
jedem Gitterpunkt zugewiesen. Da sich die
Werte gegenseitig beeinflussen, erfolgt die
Lösung iterativ.
Entsprechende Atomladungen kann man Kraftfeldparametern
entnehmen. Umgekehrt lassen sich damit Ladungen für bestimmte
Fragmente bestimmen, z.B. Ladung des Eisens in Häm-Gruppen.
8. Vorlesung SS12
Computational Chemistry
53
Poisson-Boltzmann Gleichung (5)
Anwendungen:
electrostatic steering
Beispiel: Acetylcholin an Acetylcholinesterase
8. Vorlesung SS12
Computational Chemistry
54
Poisson-Boltzmann Gleichung (6)
Anwendungen:
Elektrostatisches Potential an der
Oberfläche in Abhängigkeit des
umgebenden Salzgehaltes
Oben: Isocontourfläche von freiem
Actin
Unten: Actin mit 5 gebundenen
Ca2+-Gegenionen
8. Vorlesung SS12
Computational Chemistry
55
Poisson-Boltzmann Gleichung (7)
Berechnung des elektrostatischen Beitrags an der
Solvatationsenergie
Es sind zwei Simulationen nötig:
1. System in Vakuum (e = 1)
2. System in Lösung (e = 80)
Somit ist
D G estat 
1
2
e
 q 
i
i
 80
e 1
 i

i
8. Vorlesung SS12
Computational Chemistry
für alle Ladungen qi
im System
56
Poisson-Boltzmann Gleichung (8)
Ebenso läßt sich die freie Komplexierungsenergie eines EnzymLigand Komplexes berechnen, indem man die einzelnen Molekülsysteme aus der Lösung in ein Medium niedriger DK (em > 1)
bringt, vereinigt und anschließend zusammen solvatisiert
em
es
em
em
em
em
em
es
em
8. Vorlesung SS12
es
em
em
em
em
Computational Chemistry
57
Poisson-Boltzmann Gleichung (9)
pKa Berechnung (z.B. von Aminosäuren in Proteinen)
HA + H2O ↔ A- + H3O+ mit pH = -lg[H3O+]
pH = pKa + lg([A-]/[H3O+]) = pKa + lgKG
Henderson-Hasselbach:
Durch Umformen erhält man:
f HA ( pH ) 
[ HA ]

[ HA ]  [ A ]

1
KG 1
1

10
pH  pK a
1
f H A (p H )
1
Virtuelle Titrationskurve
0 .5
pH
0
pKa
8. Vorlesung SS12
Computational Chemistry
58
Poisson-Boltzmann Gleichung (10)
p K a (b u lk)
b e ka n n t
COOH
W a sse r
CO O -
D G w a sse r
D G n e u tra l
D G g e la d e n
COOH
P ro te in
p K a (p ro te in )
CO O -
DG
lg K  pH  pK
a
D G   kT ln K
D G ( geladen
 neutral )
  kT ln  pH  pK
a

Man erstellt eine Titrationskurve
in Abhängigkeit eines
äußeren pH und ermittelt so
den pKa der Residue
Schwierigkeiten: Wechselwirkungen mit
anderen titrierbaren Residuen
8. Vorlesung SS12
Computational Chemistry
59
Zusammenfassung Solvatation
Ionen sind im Wasser von einer Solvatationshülle umgeben,
und damit energetisch günstiger als im Vakuum (Solvatationsenergie). Deshalb sind entsprechene Aminosäurenseitenketten
auch allermeistens im geladenen Zustand anzutreffen (an der
Proteinoberfläche, bzw. gepaart als Satzbrücken im ProteinInneren).
Der zahlenmäßig größte Beitrag zur Solvatationsenrgie ist der
Born Term (Monopol). Dispersive Beiträge (Dipol-Dipol wie bei
van der Waals WW) spielen vor allem in unpolaren Medien
(kleine Dielektrizitätskonstante) eine Rolle.
Da auch entropische Beiträge (teilweise) in die Solvatationsenergie einfließen, ist es schwierig gute Übereinstimmungen
mit experimentellen Werten zu bekommen (z.B.
Bindungsaffinitäten).
8. Vorlesung SS12
Computational Chemistry
60
Scoring Funktionen (1)
Ziel: Vorhersage der biologischen Affinität einer Verbindung
Warum: Bei der Suche nach neuen pharmakologischen
Wirkstoffen wird zunächst eine virtuelle Bibliothek von
mehr als 100.000 denkbaren Verbindungen konstruiert.
Von diesen bleiben auch nach Anwendung von ADME
Filtern noch tausende übrig die in die Bindungstasche
des target Proteins passen könnten. Nur ein Bruchteil
davon kann auch tatsächlich im Labor synthetisiert
werden.  Docking Algorithmen notwendig
Das virtuelle Docking von potentiellen Wirkstoffen an ein
Enzymmodell ist der Flaschenhals im Computer Aided
Drug Design
Für ca. 50% der target Proteine von denen man die
Struktur in molekularem Detail kennt, gibt es noch keine
geeigneten Wirkstoffe
8. Vorlesung SS12
Computational Chemistry
61
Scoring Funktionen (2)
Docking ist rechenzeitaufwendig da es ein globales
Minimumproblem darstellt
starrer Ligand an starres Protein: 6 Variablen bzw. Freiheitsgrade
flexibler Ligand an starres Protein: 6 + n* Bindungen
flexibler Ligand an flexibles Protein: 6 + n* +...
8. Vorlesung SS12
Computational Chemistry
62
Scoring Funktionen (3)
 Docking benötigt eine schnell zu berechnende Bewertungsfunktion
Es bieten sich Energiefunktionen an, wie sie auch in Kraftfeldern
verwendet werden:
Intra-Ligand Konformationsterme (Bindungen, Winkel, Torsionen)
Nicht-bindende Wechselwirkungen zwischen Ligand und Enzym:
• Van der Waals Wechselwirkung (sterisch)
• Elektrostatische Wechselwirkung (Salzbrücken)
• Wasserstoffbrücken
• Solvatationsterme (Desolvatation, SASA)
• Entropische Terme (Verlust der translatorischen und rotatorischen
Freiheitsgarde bei der Bindung ans Enzym)
z.B. in FlexX und Autodock verwendet
M. Rarey et al. J. Mol. Biol. 261 (1996) 470
8. Vorlesung SS12
Computational Chemistry
63
Scoring Funktionen (4)
Prinzipielles Problem von Energiebasierten Scoring Funktionen:
Leichte Ungenauigkeiten führen zu großen Fehlern bei der Vorhersage
der Bindungskonstanten
Massenwirkungsgesetz: DG  RT ln K
5.7 kJ/mol (= 1.4 kcal/mol) bewirken Faktor 10 für K
Genauigkeit von berechneten Solvatationsenergien liegt bei
etwa 1-2 kcal/mol
Idee: Scoring Funktion wird an einer Reihe von experimentell
bekannten Enzym-Ligand Komplexen kalibriert.
Nachteil: Nicht für „neue“ Enzymsysteme verwendbar
8. Vorlesung SS12
Computational Chemistry
64
Scoring Funktionen (5)
Wissensbasierte Scoring Funktionen
Idee: Ähnliche Typen von Ligandenatomen werden häufiger zu
bestimmten Atomtypen im Protein benachbart sein.
Lit. I. Muegge & Y.C. Martin J. Med. Chem. 42 (1999) 791
Atomtypen für C: aliphatisch, aromatisch, polar, unpolar, etc.
Wesentlich mehr Atomtypen für Liganden als für Proteinatome
Aus der radialen Verteilungsfunktion zwischen Atomtypenpaaren ij wird ein potential of mean force A(ij) erstellt.
ij
 r seg
r  


Aij   k B T ln
ij
 r

bulk


PMFscore

 A r 
ij
ij
kl
Ähnlich: Drugscore Gohlke & Klebe J. Mol. Biol. 295 (2000) 377
8. Vorlesung SS12
Computational Chemistry
65
Scoring Funktionen (6)
Vergleich der Preformance von Scoring Funktionen
G. Keserű J. Comp.-Aided Mol. Design 15 (2001) 649
Vergleich anhand bekannter Cytochrom P450cam Substrate
8. Vorlesung SS12
Computational Chemistry
66
Scoring Funktionen (7)
Vergleich der Preformance von Scoring Funktionen
G. Keserű J. Comp.-Aided Mol. Design 15 (2001) 649
Vergleich anhand bekannter Cytochrom P450cam Substrate
Vergleich berechneter und tatsächlicher Bindungsaffinität
8. Vorlesung SS12
Computational Chemistry
67
Scoring Funktionen (8)
Aktueller Trend: Consensus scoring
Man bildet die Summe aus verschiedenen Scoring Funktionen
Für jede der verwendeten Scoring Funktionen wird eine
Schranke definiert, die affine (1) und nicht-affine Liganden (0)
separiert.
Das Dockingergebnis für jeden Liganden wird anhand dieser
Schranke bewertet (0 oder 1).
Diese Ganzzahlen werden für jede Scoringfunktion aufaddiert.
Bsp. Erhält man mit 4 unterschiedlichen Scoringfunktionen
mindestens 3 als Ergebnis, so wird der Ligand als bindend
betrachtet.
8. Vorlesung SS12
Computational Chemistry
68