2.4 Einige wichtige Verteilungen

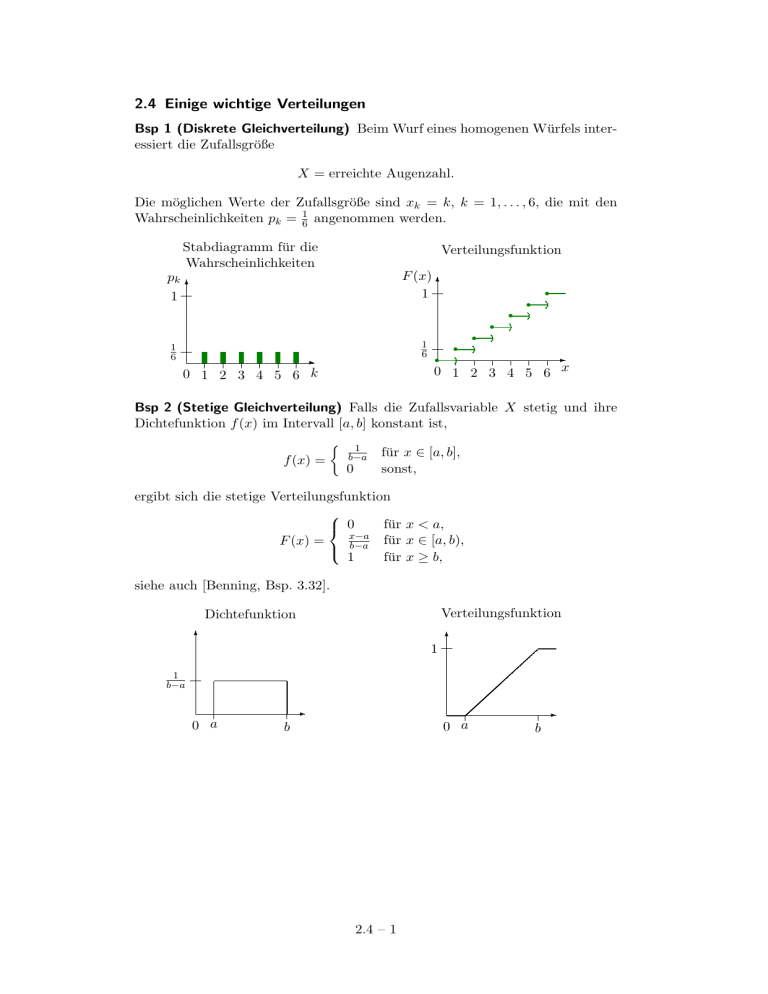
2.4 Einige wichtige Verteilungen
Bsp 1 (Diskrete Gleichverteilung) Beim Wurf eines homogenen Würfels interessiert die Zufallsgröße
X = erreichte Augenzahl.
Die möglichen Werte der Zufallsgröße sind xk = k, k = 1, . . . , 6, die mit den
Wahrscheinlichkeiten pk = 61 angenommen werden.
Stabdiagramm für die
Wahrscheinlichkeiten
Verteilungsfunktion
F (x)
6
1
pk
6
1
1
6
1
6
-
r
r
r
r
r
r
r
-
0 1 2 3 4 5 6 x
0 1 2 3 4 5 6 k
Bsp 2 (Stetige Gleichverteilung) Falls die Zufallsvariable X stetig und ihre
Dichtefunktion f (x) im Intervall [a, b] konstant ist,
1
b−a für x ∈ [a, b],
f (x) =
0
sonst,
ergibt sich die stetige Verteilungsfunktion

für x < a,
 0
x−a
für x ∈ [a, b),
F (x) =
 b−a
1
für x ≥ b,
siehe auch [Benning, Bsp. 3.32].
Verteilungsfunktion
Dichtefunktion
6
1
6
1
b−a
-
0 a
-
0 a
b
2.4 – 1
b
Bsp 3 (Binomialverteilung) Ein Bernoulli-Experiment ist ein Zufallsexperiment mit nur zwei möglichen Ergebnissen A und A, man denke z.B. an den
Münzwurf (Zahl oder Wappen) oder an eine Qualitätskontrolle (brauchbar oder
nicht). Die Wahrscheinlichkeiten seien P (A) = p und p(A) = 1 − p.
Ein solches Bernoulliexperiment werde n-mal nacheinander ausgeführt. Dann
genügt die Zufallsvariable
X = Anzahl der Versuche, in denen das Ereignis A eintritt
der Binomialverteilung . Die Wahrscheinlichkeiten sind
pk = P (X = k) =
n k
p (1 − p)n−k ,
k
k = 0, 1, 2, . . . , n.
Balkendiagramm für die Wahrscheinlichkeiten
zugehörige Verteilungsfunktion
n = 4, p = 0.5
pk
n = 4, p = 0.5
F (x)
6
1
r
1
6
r
r
r
r
0 1 2 3 4 k
n = 8, p = 0.5
F (x)
6
1
n = 8, p = 0.5
pk
1
6
r
r
r
r
0 1 2 3 4 5 6 7 8 k
6
r
r
r
r
n = 8, p = 0.1
F (x)
6
r r
1
n = 8, p = 0.1
pk
r
-
0 1 2 3 4 5 6 7 8 x
-
1
-
0 1 2 3 4 x
-
r
r
r
r
r
r
r
-
0 1 2 3 4 5 6 7 8 x
-
0 1 2 3 4 5 6 7 8 k
Siehe auch http://de.wikipedia.org/wiki/Binomialverteilung, [Papula
Bd. 3, II.6.1], [Benning, 3.6.2].
2.4 – 2
Ü 4 Wie groß ist die Wahrscheinlichkeit pk , dass beim zehnmaligen Werfen
einer Münze k-mal Wappen geworfen wird?
Lösung: Es gilt
pk =
10
k
k 10−k
1
1
−10 10
.
=2
2
2
k
k 0
1
2
3
4
5
6
7
8
9
10
pk 0.1 % 1.0 % 4.4 % 11.7 % 20.5 % 24.6 % 20.5 % 11.7 % 4.4 % 1.0 % 0.1 %
Ü 5 Bei der Qualitätskontrolle hat sich herausgestellt, dass 8 % der gefertigten
Teile nicht brauchbar sind. Wie groß ist die Wahrscheinlichkeit, dass von 10
ausgewählten Teilen (a) genau 1, (b) höchstens 3 und (c) mehr als 3 unbrauchbar
sind? (Ein einmal ausgewähltes Teil wird wieder zurückgelegt.)
Lösung: Es gilt
pk =
10
· 0.08k · 0.9210−k .
k
Die Antwort zu (a) lautet
p1 = 37, 77 %,
die Antwort zu (b) ist
F (3) =
3
X
pk = 0, 4344 + 0, 3777 + 0, 1478 + 0, 0343 = 0, 9942 = 99, 42 %,
k=0
die zu (c) ist P (X > 3) = 1 − F (3) = 0, 58 %.
Bem 6 Die Binomialverteilung entspricht dem n-maligen Ziehen mit Zurücklegen, so dass für jede Ziehung die Wahrscheinlichkeit p konstant bleibt. Beim
Ziehen ohne Zurücklegen erhält man die hypergeometrische Verteilung , siehe
z.B. http://de.wikipedia.org/wiki/Hypergeometrische_Verteilung, [Papula Bd. 3, II.6.2], [Benning, 3.6.3]. Wir wollen darauf nicht eingehen.
2.4 – 3
Bsp 7 (Poissonverteilung) Die Verteilung einer diskreten Zufallsgröße X, bei
der
λk −λ
pk = P (X = k) =
e , k = 0, 1, 2, . . . , λ > 0,
k!
ist heißt Poisson-Verteilung mit dem Parameter λ.
Balkendiagramm für die
Wahrscheinlichkeiten
λ=1
λ=1
F (x)
6
1
pk
1
zugehörige Verteilungsfunktion
6
r
r
r
r
r
r
r
r
r
-
0 1 2 3 4 5 6 7 8 x
-
0 1 2 3 4 5 6 7 8 k
λ=6
λ=6
F (x)
6
1
pk
1
6
r
r
r
r
r
r
r
r
r
-
0 1 2 3 4 5 6 7 8 x
-
0 1 2 3 4 5 6 7 8 k
Die Poisson-Verteilung geht aus einer Folge von binomialverteilten Zufallsgrößen mit den Parametern n und p durch den Grenzübergang n → ∞ hervor,
wenn man gleichzeitig p so variiert, dass np = k konstant bleibt.
Für p ≤ 0, 08 und n ≥ 1500p kann die Binomialverteilung mit i. Allg. ausreichender Genauigkeit durch die Poisson-Verteilung ersetzt werden, deren Auswertung einfacher ist.
Konkrete Anwendungen sind:
• Ein Kaufhaus wird an einem Samstag durchschnittlich alle 10 Sekunden
von einem Kunden betreten. Die Wahrscheinlichkeit dafür, dass in der
nächsten Minute (= 6 · 10 Sekunden) genau 9 Kunden das Kaufhaus betreten, wird durch p9 = P (X = 9) mit λ = 6 beschrieben.
• In der Natur verhält sich zum Beispiel der radioaktive Zerfall nach der
Poisson-Verteilung. Gibt X die Anzahl der Atomkerne an, die in einer
Sekunde zerfallen, dann ist X Poisson-verteilt. Der Parameter λ gibt an,
wieviele Atomkerne in einer Sekunde durchschnittlich zerfallen.
Siehe auch http://de.wikipedia.org/wiki/Poisson-Verteilung,
[Papula Bd. 3, II.6.3], [Benning, 3.6.4].
2.4 – 4
Aufg 8 Von den mundgeblasenen Gläsern einer Glashütte ist bekannt, dass im
Durchschnitt 0,2 Fehler pro Glas auftreten. Die diskrete Zufallsvariable
X = Zahl der Unreinheiten in einem Glas
ist annähernd poissonverteilt mit dem Parameter λ = 0,2. Man bestimme die
Wahrscheinlichkeit, dass ein Glas (a) keinen Fehler, (b) genau einen Fehler und
(c) mindestens zwei Fehler hat.
Lösung: Es ist (a)
P (X = 0) =
0,20 −0,2
e
= 0, 8187,
0!
P (X = 1) =
0,21 −0,2
e
= 0, 1637
1!
(b)
und (c)
P (X ≥ 2) = 1 − P (X ≤ 1) = 1 − 0, 8187 − 0, 1637 = 0, 0175.
2.4 – 5
Bsp 9 (Normalverteilung) Eine Zufallsgröße X mit der Dichtefunktion
(x−µ)2
1
f (x) = √ e− 2σ2
σ 2π
heißt normalverteilt , genauer (µ, σ)-normalverteilt . Die Verteilungsfunktion
lautet entsprechend
Z x
(t−µ)2
1
F (x) = √
e− 2σ2 dt.
σ 2π −∞
Von der Standardnormalverteilung spricht man, wenn die Normalverteilung die
Parameter µ = 0 und σ = 1 besitzt.
zugehörige Verteilungsfunktion
Dichtefunktion, µ = 0, σ = 1
y
–2
–1
0.8
0.5
y
0
1
2
–2
x
–1
0.4
0
1
2
x
Die Kurve zur Dichtefunktion ist auch als Glockenkurve bekannt.
0.4
0.3
y
0.2
0.1
–3
–2
–1
0
1
2
3
x
Siehe auch http://de.wikipedia.org/wiki/Normalverteilung,
[Papula Bd. 3, II.6.4], [Benning, 3.6.5].
2.4 – 6