2. Konsumententheorie - WWZ

2. Konsumententheorie
Georg Nöldeke
WWZ, Universität Basel
Intermediate Microeconomics, HS 11
2. Konsumententheorie
1/99
2.1 Einleitung
Wir betrachten durchweg eine Situation, in der es nur zwei
Güter gibt, die im Allgemeinen mit Gut 1 und Gut 2
bezeichnet werden.
Ein Güterbündel x ist durch die Angabe von Mengen der
beiden Güter beschrieben: x = (x1 , x2 ) mit x1 ≥ 0 und x2 ≥ 0.
Der Konsument verfügt über ein Budget in Höhe von m > 0
Geldeinheiten, welches ihm zum Kauf der beiden Güter
zur Verfügung steht.
Die Preise der beiden Güter sind durch p = (p1 , p2 ) mit
p1 > 0 und p2 > 0 gegeben.
Das Budget m und die Preise p1 , p2 werden als
vorgegeben betrachtet: m und p sind exogen.
Die Entscheidung des Konsumenten besteht in der
Auswahl eines Güterbündels: x ist endogen.
2 / 99
2.2 Präferenzen
Ausgangspunkt der folgenden Modellierung ist die
Vorstellung, dass wir für einen Konsumenten, der zwischen
zwei Güterbündeln x und y auszuwählen hat, beobachten
können, ob er
1. das Güterbündel x als besser erachtet.
2. das Güterbündel y als besser erachtet.
3. die beiden Güterbündel für gleich gut erachtet.
Wir schreiben in den jeweiligen Fällen:
1. x y (“x wird y streng vorgezogen.”)
2. y x (“y wird x streng vorgezogen.”)
3. x ∼ y (“x und y sind indifferent”)
und nehmen an, dass für gegebene Güterbündel x und y
höchstens eine dieser Aussagen zutreffend ist.
3 / 99
2.2 Präferenzen
Man definiert
x y ⇔ x y oder x ∼ y,
und liest die Beziehung als “x wird y vorgezogen.”
Eine Präferenzrelation, die ebenfalls mit bezeichnet
wird, ist dadurch beschrieben, dass sie für jedes Paar von
Güterbündeln x und y angibt, ob die Beziehung x y gilt
oder nicht.
Beachte: Aus Kenntnis der Präferenzrelation kann man
die Indifferenzrelation ∼ und die strenge Präferenzrelation
rekonstruieren.
Gilt z.B. x y während die Beziehung y x nicht gilt, so
folgt x y.
4 / 99
2.2 Präferenzen
Definition (Vollständigkeit)
Eine Präferenzrelation heisst vollständig, wenn für alle
Güterbündel x und y gilt:
x y oder y x (oder beides).
Definition (Transitivität)
Eine Präferenzrelation heisst transitiv, wenn für alle
Alternativen x, y und z gilt:
x y und y z ⇒ x z.
5 / 99
2.2 Präferenzen
Definition (Rationalität)
Eine Präferenzrelation heisst rational, wenn sie vollständig
und transitiv ist.
Gegeben eine rationale Präferenzrelation und ein
Güterbündel x = (x1 , x2 ) definiert man die Indifferenzkurve
I(x) als die Menge aller Güterbündel, die indifferent zu x
sind:
I(x) = {y = (y1 , y2 ) | y ∼ x}
6 / 99
2.2 Präferenzen
Im Regelfall wird unterstellt, dass Präferenzrelationen nicht
nur rational sind, sondern weitere Eigenschaften
aufweisen:
1. Stetigkeit und Differenzierbarkeit der Präferenzrelation:
Indifferenzkurven haben keine “Sprünge” und keine
“Knicke.”
2. Strenge Monotonie der Präferenzrelation: Mehr ist besser.
3. Strenge Konvexität der Präferenzrelation: Mischungen sind
besser als Extreme.
Stetigkeit und Differenzierbarkeit ist eine “technische”
Annahme, die wir nicht weiter formalisieren werden.
7 / 99
2.2 Präferenzen
Zur Vereinfachung verwenden wir die folgende Notation
und Terminologie:
x ≥ y bedeutet, dass x1 ≥ y1 und x2 ≥ y2 gilt: x ist grösser als
y.
x > y bedeutet, dass x1 > y1 und x2 > y2 gilt: x ist streng
grösser als y.
Ein Güterbündel mit x > 0 bezeichnen wir als inneres
Güterbündel.
Definition (Monotonie und strenge Monotonie)
Sei x 6= y. Eine rationale Präferenzrelation heisst monoton,
wenn aus x ≥ y folgt, dass x y gilt. Folgt für innere
Güterbündel zudem x y, so heisst die Präferenzrelation
streng monoton.
8 / 99
2.2 Präferenzen
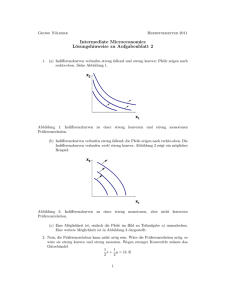
Abbildung: Ist eine Präferenzrelation streng monoton, so sind die
Indifferenzkurven durch innere Güterbündel streng fallende
Funktionen.
9 / 99
2.2 Präferenzen
Die Güterbündel z, die auf der Verbindungslinie zwischen
zwei Güterbündeln x und y liegen, lassen sich
mathematisch als sogenannte konvexe Kombinationen von
x und y beschreiben.
Für alle Güterbündel x, y und reele Zahlen 0 ≤ α ≤ 1
definiert man
αx + (1 − α)y = (αx1 + (1 − α)y1 , αx2 + (1 − α)y2 ).
Gilt z = αx + (1 − α)y für 0 < α < 1, so bezeichnet man z als
eine konvexe Kombination von x und y.
Definition (Konvexität und strenge Konvexität)
Eine Präferenzrelation heisst konvex, wenn für alle
Güterbündel x 6= y und konvexen Kombinationen z dieser beiden
Güterbündel aus x y folgt, dass auch z y gilt. Gilt für innere
Güterbündel zudem z y, so heisst die Präferenzrelation
streng konvex.
10 / 99
2.2 Präferenzen
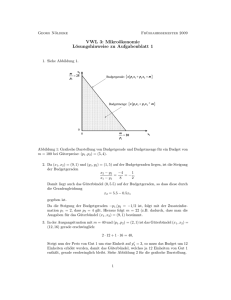
Abbildung: Eine Indifferenzkurve einer streng konvexen
Präferenzrelation. Alle Güterbündel auf der Verbindungslinie
zwischen den indifferenten Güerbündeln x und y werden diesen
Güterbündeln streng vorgezogen. Hier für das Güterbündel
z = 0.5x + 0.5y dargestellt.
11 / 99
2.2 Präferenzen
Abbildung: Indifferenzkurve einer nicht-konvexen, aber streng
monotonen Präferenzrelation. Das Güterbündel z liegt auf der
Verbindungslinie zwischen x und y, so dass bei Konvexität z y
gelten müsste. Es gilt aber y z.
12 / 99
2.2 Präferenzen
Definition (Artigkeit)
Eine rationale Präferenzrelation heisst artig, wenn sie
differenzierbar, streng monoton und streng konvex ist.
Artigkeit besagt, dass
die Indifferenzkurven sich als differenzierbare, streng
fallende und streng konvexe Funktionen von x1 darstellen
lassen.
Güterbündel, die “rechts oberhalb” einer Indifferenzkurve
liegen, den Güterbündeln auf der Indifferenzkurve
vorgezogen werden.
Wir werden im Folgenden nur artige Präferenzrelationen
betrachtet.
13 / 99
2.2 Präferenzen
Abbildung: Eine Indifferenzkurve einer artigen Präferenzrelation.
14 / 99
2.3 Die Grenzrate der Substitution
Definition (Grenzrate der Substitution)
Die Steigung der Indifferenzkurve I(x) an der Stelle x heisst die
Grenzrate der Substitution an der Stelle x. Sie wird mit
GRS(x) bezeichnet.
Die Grenzrate der Substitution misst (im Sinne eines
Grenzwertes) das Verhältnis ∆x2 /∆x1 , in dem die Mengen
der beiden Güter gegeneinander ausgetauscht werden
können, so dass der Konsument indifferent bleibt.
Oftmals ist es nützlich, den Absolutwert der Grenzrate der
Substitution zu betrachten. Diesen bezeichnen wir als die
marginale Zahlungsbereitschaft (für Gut 1).
15 / 99
2.3 Die Grenzrate der Substitution
Satz
Für eine artige Präferenzrelation gilt für alle x > 0:
1. Die Grenzrate der Substitution ist streng negativ:
GRS(x) < 0.
2. Die marginale Zahlungsbereitschaft ist streng fallend
entlang einer Indifferenzkurve: x ∼ y und x1 > y1 impliziert
| GRS(x) |<| GRS(y) |.
16 / 99
2.3 Die Grenzrate der Substitution
Abbildung: Indifferenzkurve einer artigen Präferenzrelation. Es gilt
GRS(x) < 0 und der Absolutwert | GRS(x) | ist um so kleiner, je grösser
x1 ist.
17 / 99
2.3 Die Grenzrate der Substitution
Abbildung: Indifferenzkurve einer nicht-konvexen Präferenzrelation.
Die marginale Zahlungsbereitschaft steigt bei einer Bewegung
entlang der Indifferenzkurve.
18 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Rationale Präferenzrelationen lassen sich durch eine
sogenannte Nutzenfunktion darstellen.
Die Nutzendarstellung einer Präferenzrelation erfolgt
dadurch, dass besseren Alternativen ein höherer Wert der
Nutzenfunktion zugeordnet wird.
19 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Definition (Nutzenfunktion)
Eine Nutzenfunktion u ordnet jedem Güterbündel x eine reele
Zahl u(x) zu: die Nutzenbewertung des Güterbündels x.
Definition (Nutzendarstellung)
Eine Nutzenfunktion u stellt eine Präferenzrelation dar, falls
für alle Güterbündel x und y gilt:
x y ⇔ u(x) ≥ u(y)
20 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Bei der Nutzendarstellung kommt es nur darauf an, dass
die Nutzenfunktion die Güterbündel genauso ordnet, wie
die Präferenzrelation.
Definition (Streng monotone Transformation)
Eine Nutzenfunktion v heisst eine streng monotone
Transformation einer Nutzenfunktion u, wenn es eine streng
steigende Funktion f : R → R gibt, so dass für alle Güterbündel
x gilt:
v(x) = f (u(x)).
21 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Satz (Ordinalität der Nutzendarstellung)
Wenn u eine Nutzendarstellung der Präferenzrelation ist,
dann stellt auch jede streng monotone Transformation v von u
die Präferenzrelation dar.
Die Ordinalität der Nutzendarstellung impliziert, dass es
keinen Sinn macht, Eigenschaften der Nutzenfunktion, die
durch eine streng monotone Transformation verändert
werden, mit Blick auf die Ziele eines Entscheiders zu
interpretieren.
22 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Aus der Angabe einer Nutzenfunktion u lassen sich die
Indifferenzkurven der dargestellten Präferenzrelation
bestimmen.
Die Indifferenzkurve zu x ist:
I(x) = {y = (y1 , y2 ) | u(y) = u(x)}
Insbesondere entsprechen die Indifferenzkurven von den Niveaulinien von u.
Eine beliebige Indifferenzkurve ist durch die Gleichung
u(x) = k bestimmt.
Unterschiedliche Indifferenzkurven korrespondieren zu
unterschiedlichen Werten der Konstanten k.
23 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Definition (Grenznutzen)
Die partielle Ableitung ∂∂u(x)
xi einer differenzierbaren
Nutzenfunktion bezeichnet man als den Grenznutzen des i-ten
Gutes (an der Stelle x).
Beachte: Der Grenznutzen ist kein ordinales Konzept, d.h.
unterschiedliche Nutzendarstellungen der gleichen
Präferenzrelation führen zu unterschiedlichen
Grenznutzen.
Dennoch ist der Grenznutzen ein hilfreiches Konzept, da er
zur Bestimmung der Grenzrate der Substitution der durch
u dargestellten Präferenzordnung verwendet werden kann.
24 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Satz
Sei u eine differenzierbare Nutzenfunktion mit streng positiven
Grenznutzen ∂ u(x)/∂ xi > 0. Dann gilt für die Grenzrate der
Substitution der durch u dargestellten Präferenzrelation :
GRS(x) = −
∂ u(x)/∂ x1
.
∂ u(x)/∂ x2
Die marginale Zahlungsbereitschaft ist also gleich dem
Verhältnis der Grenznutzen der beiden Güter.
Anmerkung: Ergebnis folgt aus dem Satz über implizite
Funktionen, der auf die Gleichung u(x1 , x2 ) = k angewendet
wird.
25 / 99
2.4 Nutzendarstellung von Präferenzrelationen
Frage
Wie erkennt man, ob eine differenzierbare Nutzenfunktion eine
artige Präferenzrelation darstellt?
1. Die Grenznutzen beider Güter sind für alle x > 0 streng
positiv.
2. Das Verhältnis der Grenznutzen ist für alle x > 0 bei einer
Bewegung entlang einer Niveaulinie streng fallend in x1 die Nutzenfunktion ist streng quasikonkav.
Definition (Artige Nutzenfunktion)
Eine differenzierbare Nutzenfunktion heisst artig, wenn sie
streng quasikonkav ist und die Grenznutzen beider Güter für
x > 0 streng positiv sind.
26 / 99
2.5 Beispiele für Nutzenfunktionen
Definition (Cobb-Douglas-Präferenzen)
Eine Präferenzrelation heisst Cobb-Douglas, wenn sie durch
eine sogenannte Cobb-Douglas-Nutzenfunktion der Form
u(x1 , x2 ) = x1c · x2d mit c > 0 und d > 0
dargestellt werden kann.
Die Bedeutung von Cobb-Douglas-Präferenzen liegt darin,
dass Cobb-Douglas-Nutzenfunktionen recht leicht zu
handhaben sind und daher zur Illustration vieler der
folgenden Überlegungen und Definitionen verwendet
werden können.
27 / 99
2.5 Beispiele für Nutzenfunktionen
Eine Cobb-Douglas-Präferenzrelation mit der
Nutzendarstellung
u(x1 , x2 ) = x1c · x2d mit c > 0 und d > 0
wird ebenfalls durch die folgenden Nutzenfunktionen
dargestellt:
u(x1 , x2 ) = x1a x21−a
u(x1 , x2 ) = a ln(x1 ) + (1 − a) ln(x2 ),
wobei
c
.
c+d
Wie wir noch sehen werden, besitzt der Parameter a in
diesen Darstellungen eine unmittelbare ökonomische
Interpretation.
a=
28 / 99
2.5 Beispiele für Nutzenfunktionen
Cobb-Douglas Präferenzrelationen sind artig:
1. Die Cobb-Douglas Nutzenfunktion ist differenzierbar.
2. Für x > 0 sind die partiellen Ableitungen der
Nutzendarstellung u(x1 , x2 ) = a ln(x1 ) + (1 − a) ln(x2 ) streng
positiv
∂ u(x)
a
∂ u(x) 1 − a
=
> 0,
=
> 0.
∂ x1
x1
∂ x2
x2
3. Das Verhältnis der Grenznutzen
a x2
∂ u(x)/∂ x1
=
∂ u(x)/∂ x2 1 − a x1
ist streng fallend in x1 und streng steigend in x2 und daher
streng fallend bei einer Bewegung entlang einer
Niveaulinie.
29 / 99
2.5 Beispiele für Nutzenfunktionen
Cobb-Douglas-Präferenzen: Niveaulinien u(x1 , x2 ) = k der
Nutzenfunktion u(x1 , x2 ) = x1 x2 . Beachte: Für alle k > 0 verlaufen
die Indifferenzkurven streng fallend und streng konvex - die
Präferenzrelation ist artig.
30 / 99
2.5 Beispiele für Nutzenfunktionen
Definition (Quasilineare Präferenzen)
Eine Präferenzrelation heisst quasilinear (im zweiten Gut),
wenn sie durch eine sogenannte quasilineare Nutzenfunktion
der Form
u(x1 , x2 ) = v(x1 ) + x2
dargestellt werden kann.
Niveaulinien einer quasilinearen Nutzenfunktion:
v(x1 ) + x2 = k ⇔ x2 = k − v(x1 ).
Dies bedeutet, dass sich die verschiedenen
Indifferenzkurven einer quasilinearen Präferenzrelation nur
durch die Höhe des vertikalen Achsenabschnitts k − v(0)
voneinander unterscheiden.
31 / 99
2.5 Beispiele für Nutzenfunktionen
Quasilineare Präferenzrelation: Die Indifferenzkurven
ergeben sich aus der vertikalen Verschiebung einer einzigen
Indifferenzkurve.
32 / 99
2.5 Beispiele für Nutzenfunktionen
Um eine quasilineare Präferenzrelation zu beschreiben,
genügt es, die Funktion v anzugeben, welche jeder Menge
von Gut 1 eine reele Zahl zuordnet.
Gilt v(0) = 0, so hat diese Funktion eine einfache
Interpretation: v(x1 ) ist die Zahlungsbereitschaft des
Konsumenten dafür, die Menge x1 anstatt die Menge 0 von
Gut 1 zu erhalten.
Diese Zahlungsbereitschaft wird in Einheiten von Gut 2
gemessen.
Beachte:
Zahlungsbereitschaft und marginale Zahlungsbereitschaft
sind unabhängig davon, wieviele Einheiten x2 in einem
Güterbündel enthalten sind.
33 / 99
2.5 Beispiele für Nutzenfunktionen
Die quasilineare Nutzenfunktionen u(x1 , x2 ) = v(x1 ) + x2 stellt
eine artige Präferenzrelationen dar, wenn v differenzierbar mit
streng positiver erster Ableitung v0 und streng negativer
Ableitung v00 ist:
1. Die partiellen Ableitungen der quasilinearen
Nutzenfunktion sind streng positiv:
∂ u(x)
∂ u(x)
= v0 (x1 ) > 0,
= 1 > 0.
∂ x1
∂ x2
2. Das Verhältnis der Grenznutzen ist v0 (x1 ). Gilt v00 (x1 ) < 0,
so ist dieses streng fallend bei einer Bewegung entlang
einer Niveaulinie.
34 / 99
2.6 Die Budgetbeschränkung
Preise und Budget bestimmen die Möglichkeiten des
Konsumenten: Er kann sich diejenigen Güterbündel
leisten, die in der Budgetmenge
B(p, m) = {x = (x1 , x2 ) | p1 x1 + p2 x2 ≤ m}
liegen.
Man nennt diese Güterbündel auch erschwinglich.
Die Ungleichung p1 x1 + p2 x2 ≤ m besagt, dass die
Ausgaben für ein Güterbündel x bei Güterpreisen p das
Budget m nicht übersteigen. Sie wird als
Budgetbeschränkung bezeichnet.
Die Budgetgerade beschreibt diejenigen Güterbündel, die
gerade erschwinglich sind
p1 x1 + p2 x2 = m,
d.h. die Ausgaben entsprechen dem Budget.
35 / 99
2.6 Die Budgetbeschränkung
Die Budgetgerade
p1 x1 + p2 x2 = m ⇔ x2 =
m p1
− x1
p2 p2
beschreibt tatsächlich eine Gerade mit
Steigung: −p1 /p2 < 0.
Horizontaler Achsenabschnitt: m/p1 > 0.
Vertikaler Achsenabschnitt: m/p2 > 0.
Beachte: Der Konsument kann sich alle Güterbündel
leisten, die “links unterhalb” der Budgetgeraden liegen.
36 / 99
2.6 Die Budgetbeschränkung
Ökonomische Interpretation der Steigung der
Budgetgerade:
Die Steigung −p1 /p2 ist negativ, da der Konsument bei
einer Bewegung entlang der Budgetgeraden etwas von Gut
2 aufgeben muss, um zusätzliche Einheiten von Gut 1 zu
erlangen.
Der Absolutwert der Steigung, p1 /p2 , gibt an, wieviele
Einheiten von Gut 2 der Konsument aufgeben muss, um
eine zusätzliche Einheit von Gut 1 zu erhalten. Dieser
sogenannte relative Preis stellt also die
Opportunitätskosten einer zusätzlichen Einheit von Gut 1
dar.
Ökonomische Interpretation der Achsenabschnitte der
Budgetgerade:
Die Achsenabschnitte geben an, wieviele Einheiten des
jeweiligen Gutes sich der Konsument maximal leisten kann,
wenn er auf den Konsum des anderen Gutes verzichtet.
37 / 99
2.6 Die Budgetbeschränkung
Eine Veränderung des Budgets führt zu einer
Parallelverschiebung der Budgetgeraden.
Beispiel: Budget steigt ⇒ beide Achsenabschnitt steigen
um den Prozentsatz der Budgeterhöhung an.
Eine Veränderung eines Preises führt zu einer Drehung
der Budgetgeraden um den Achsenabschnitt des Gutes,
dessen Preis unverändert bleibt.
Beispiel: Preis von Gut 1 steigt ⇒ horizontaler
Achsenabschnitt wird kleiner; vertikaler Achsenabschnitt
bleibt unverändert.
Eine Veränderung aller Preise und des Budgets um den
gleichen Prozentsatz lässt die Budgetgerade und damit die
Budgetmenge unverändert.
Beispiel: Werden alle Preise und das Budget in Rappen
statt in Franken gemessen, so ändert sich nichts an den
Güterbündeln, die der Konsument sich leisten kann.
38 / 99
2.6 Die Budgetbeschränkung
Anstatt Budget und Preise in einer fixen Geldeinheit zu
messen, kann man auch den Preis von Gut 2 als
Recheneinheit für die Geldgrössen wählen.
Tut man dies, so bezeichnet man Gut 2 als Numeraire und
setzt p2 = 1.
Das Budget m gibt dann an, wieviele Einheiten des
Numeraire sich der Konsument maximal leisten kann.
Der Preis p1 von Gut 1 gibt dann den relativen Preis von
Gut 1 an; er entspricht der Anzahl der Einheiten des
Numeraires, auf welche der Konsument für eine zusätzliche
Einheit von Gut 1 verzichten muss.
Beachte: Die Budgetgerade bleibt unverändert, wenn man
statt (p1 , p2 , m) die Werte (p1 /p2 , 1, m/p2 ) einsetzt.
Es ist also stets möglich, Gut 2 als Numeraire zu wählen,
ohne etwas daran zu ändern, welche Güterbündel
erschwinglich sind.
39 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Wir gehen davon aus, dass der Konsument bei gegebenen
Preisen p = (p1 , p2 ) > 0 und gegebenem Budget m > 0 ein
Güterbündel wählt, welches optimal im Sinne der
folgenden Definition ist.
Definition (Optimales Güterbündel)
Sei eine rationale Präferenzrelation. Ein Güterbündel
x∗ ∈ B(p, m) ist optimal in der Budgetmenge B(p, m), wenn es
allen anderen Güterbündeln in der Budgetmenge vorgezogen
wird:
x ∈ B(p, m) ⇒ x∗ x.
40 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Satz
Ist eine Präferenzrelation artig, so gibt es in jeder
Budgetmenge B(p, m) mit p > 0 und m > 0 genau ein optimales
Güterbündel. Dieses liegt auf der Budgetgeraden, d.h. es gilt
p1 x1∗ + p2 x2∗ = m.
Die Existenz eines optimalen Güterbündels wird durch die
Annahme der Stetigkeit der Präferenzrelation gesichert.
Eindeutigkeit folgt aus der Annahme der strengen
Konvexität der Präferenzrelation.
Die Annahme der strengen Monotonie sichert, dass das
optimale Güterbündel auf der Budgetgeraden liegen muss.
41 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Abbildung: Die Lösung eines Konsumentenproblems bei einer artigen
Präferenzrelation. In der dargestellten Budgetmenge ist x∗ das
einzige optimale Güterbündel. Es wird allen anderen Güterbündeln in
der Budgetmenge, wie z.B. dem mit x markierten Güterbündel, streng
vorgezogen.
42 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Abbildung: Ein Beispiel mit zwei optimalen Güterbündeln. Beachten
Sie, dass die Präferenzrelation nicht konvex ist, da ansonsten das als
“nicht optimal” markierte Güterbündel vorgezogen sein müsste.
43 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Abbildung: Das innere Güterbündel x liegt auf der Budgetgeraden. Es
ist nicht optimal, da die Indifferenzkurve durch x die Budgetgeraden
schneidet und es somit Güterbündel in der Budgetmenge gibt, die x
streng vorgezogen werden. Hier liegen diese Güterbündel in dem
grün markierten Bereich.
44 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Satz
Ist eine Präferenzrelation artig, so ist ein Güterbündel x∗ > 0,
welches auf der Budgetgeraden liegt, genau dann optimal,
wenn die Grenzrate der Substitution bei diesem Güterbündel
mit der Steigung der Budgetgeraden übereinstimmt:
GRS(x∗ ) = −
p1
.
p2
Ökonomischer formuliert, besagt die
Optimalitätsbedingung aus diesem Satz, dass die
marginale Zahlungsbereitschaft für Gut 1 mit dem relativen
Preis von Gut 1 übereinstimmt.
45 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Beachte die Annahme x∗ > 0 in der Formulierung des
Satzes – es handelt sich um eine Charakterisierung
sogenannter innerer Lösungen des
Konsumentenproblems.
Gibt es kein Güterbündel, welches die
Optimalitätsbedingung erfüllt, so muss es sich bei der
Lösung des Konsumentenproblems um eine sogenannte
Randlösung handeln: entweder x∗ = (m/p1 , 0) oder
x∗ = (0, m/p2 ) ist optimal.
46 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Satz (Nutzenmaximierung)
Sei u eine Nutzendarstellung der Präferenzrelation . Das
Güterbündel x∗ ist genau dann optimal in der Budgetmenge
B(p, m), wenn es das folgende Nutzenmaximierungsproblem
löst:
max u(x) unter der Nebenbedingung p1 x1 + p2 x2 ≤ m.
x≥0
Für eine gegebene Nutzenfunktion u kann man optimale
Güterbündel also explizit durch Lösung des
Nutzenmaximierungsproblems bestimmen.
Wir befassen uns daher im folgenden mit der Frage, wie
man ein Nutzenmaximierungsproblem löst.
47 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Satz
Ist u eine artige Nutzenfunktion. Liegt das Güterbündel x∗ auf
der Budgetgeraden,
p1 x1∗ + p2 x2∗ = m,
(1)
und erfüllt es die Bedingung erster Ordnung,
p1
∂ u(x1∗ , x2∗ )/∂ x1
= ,
∗
∗
∂ u(x1 , x2 )/∂ x2
p2
(2)
so ist es die einzige Lösung des Nutzenmaximierungsproblems.
48 / 99
2.7 Optimale Güterbündel und Nutzenmaximierung
Für artige Nutzenfunktionen kann man zur Lösung des
Nutzenmaximierungsproblems also wie folgt verfahren:
1. Suche ein Güterbündel, welches Gleichungen (1) und (2)
erfüllt. Ist die Suche erfolgreich, so ist die Lösung des
Nutzenmaximierungsproblems bestimmt.
2. Gibt es kein solches Güterbündel, so muss eine
Randlösung vorliegen. Vergleiche u(m/p1 , 0) und u(0, m/p2 ),
um zu bestimmen, welches dieser beiden Güterbündel den
grösseren Nutzen liefert – dieses ist die Lösung des
Nutzenmaximierungsproblems.
49 / 99
2.8 Beispiele für Nutzenmaximierung
Cobb-Douglas-Nutzenfunktion: u(x1 , x2 ) = x1a x21−a mit
0 < a < 1.
Die Gleichungen
p1 x1∗ + p2 x2∗ = m
und
GRS(x1∗ , x2∗ ) = −
ax2∗
p1
=−
∗
(1 − a)x1
p2
besitzen die eindeutige Lösung
x1∗ = am/p1 > 0, x2∗ = (1 − a)m/p2 > 0.
Dieses Güterbündel ist also die eindeutige Lösung des
Nutzenmaximierungsproblems.
Beachte: Der Parameter a stellt den Anteil des Budgets
dar, den der Konsument füt Gut 1 ausgibt.
50 / 99
2.8 Beispiele für Nutzenmaximierung
Artige quasilineare Nutzenfunktion u(x1 , x2 ) = v(x1 ) + x2 .
Gibt es ein Güterbündel x∗ ≥ 0, welches die Bedingungen
v0 (x1∗ ) = p1 /p2 und x2∗ = (m − p1 x1∗ )/p2
erfüllt, so ist dieses die einzige Lösung des
Nutzenmaximierungsproblems.
Gibt es kein solches Güterbündel, so tritt eine
Randlösung auf:
1. Gilt v0 (0) ≤ p1 /p2 , so ist (x1∗ , x2∗ ) = (0, m/p2 ) die einzige
Lösung des Nutzenmaximierungsproblems.
2. Gilt v0 (m/p1 ) ≥ p1 /p2 , so ist (x1∗ , x2∗ ) = (m/p1 , 0) die einzige
Lösung des Nutzenmaximierungsproblems.
51 / 99
2.8 Beispiele für Nutzenmaximierung
Abbildung: Optimale Güterbündel für eine artige, quasilineare
Präferenzrelation: Für die rote Budgetgerade ist das innere
Güterbündel x0 optimal. Hier gilt v0 (x10 ) = p1 /p2 . Für die schwarze und
die grüne Budgetgerade resultiert die Randlösung x∗ = (0, m/p2 ).
52 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Die Nachfragefunktion eines Konsumentens beschreibt,
welches Güterbündel x der Konsument in Abhängigkeit von
den Güterpreisen p > 0 und seinem Budget m > 0 wählt.
Formal ist die Nachfragefunktion eines Konsumenten also
eine Funktion f , die jedem (p, m) > 0 das nachgefragte
Güterbündel x = f (p, m) zuordnet.
Wir schreiben
x1 = f1 (p1 , p2 , m), x2 = f2 (p1 , p2 , m)
für die nachgefragte Menge des ersten, bzw. des zweiten
Gutes und bezeichnen die entsprechend definierte
Funktion als die Nachfragefunktion von Gut i.
53 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Im Folgenden ist zur Vereinfachung unterstellt, dass
die betrachteten Nachfragefunktionen differenzierbar sind.
die betrachteten Budgetsituationen so sind, dass streng
positive Mengen beider Güter nachgefragt werden.
Die partiellen Ableitungen der Nachfragefunktion
bezeichnen wir mit
∂ fi (p,m)
∂ pj :
Änderung der nachgefragten Menge von Gut i bei
Erhöhung des Preises von Gut j.
∂ fi (p,m)
∂ m : Änderung der nachgefragten Menge von Gut i bei
einer Erhöhung des Budgets.
54 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Einkommenselastizität (der Nachfrage) von Gut i:
ξi (p, m) =
∂ fi (p, m) m
.
∂m
fi (p, m)
Ausgabenanteil von Gut i:
θi (p, m) =
pi fi (p, m)
.
m
Elastizität der Nachfrage von Gut i bei einer Änderung des
Preises von Gut j:
εi j (p, m) =
∂ fi (p, m) p j
.
∂ pj
fi (p, m)
Für i = j ist dieses die Eigenpreiselastizität; für i 6= j die
Kreuzpreiselastizität.
55 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Definition (Normale und inferiore Güter)
(Die Nachfrage von) Gut i heisst normal, wenn die
nachgefragte Menge des Gutes mit steigendem
Einkommen zunimmt: ξi (p, m) > 0.
(Die Nachfrage von) Gut i heisst inferior, wenn die
nachgefragte Menge des Gutes mit steigendem
Einkommen streng abnimmt: ξi (p, m) < 0
Ob ein Gut normal oder inferior ist, hängt im Allgemeinen
von der betrachteten Budgetsituation ab.
Gilt ξi (p, m) = 0 bezeichnet man die Nachfrage von Gut i
als einkommensunabhängig.
56 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Ob ein Gut normal, inferior oder einkommensunabhängig
ist, hängt davon ab, wie sich die marginale
Zahlungsbereitschaft bei Änderung der Menge des
anderen Gutes verändert:
Hängt die marginale Zahlungsbereitschaft für Gut 1 nicht
von der Menge von Gut 2 ab, so ist Gut 1
einkommensunabhängig. Das gilt bei quasilinearen
Präferenzen.
Steigt die marginale Zahlungsbereitschaft für Gut 1 bei
einem Anstieg der Menge von Gut 1, so ist Gut 1 normal.
Fällt die marginale Zahlungsbereitschaft für Gut 1 bei
einem Anstieg der Menge von Gut 2, so ist Gut 1 inferior.
Die folgenden Abbildungen illustrieren diese
Zusammenhänge.
57 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Quasilineare Präferenzrelation: Die Nachfrage von Gut 1 ist
einkommensunabhängig, da die Steigung der Indifferenzkurven
nicht von x2 abhängt.
58 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Gut 1 ist normal: Bei einem Anstieg von x2 steigt die marginale
Zahlungsbereitschaft. Dies führt dazu, dass die nachgefrage
Menge von Gut 1 mit steigendem Einkommen zunimmt.
59 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Gut 1 ist inferior: Bei einem Anstieg von x2 fällt die marginale
Zahlungsbereitschaft. Dieses führt dazu, dass die nachgefragte
Menge von Gut 1 mit steigendem Einkommen fällt.
60 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Definition (Gewöhnliche Güter und Giffen-Güter)
Gut i heisst gewöhnlich, wenn die nachgefragte Menge
des Gutes mit steigendem Preis des betrachteten Gutes
abnimmt: εii (p, m) ≤ 0
Gut i heisst Giffen, wenn die nachgefragte Menge des
Gutes mit steigendem Preis des betrachteten Gutes
zunimmt: εii (p, m) > 0.
Auch bei dieser Definition gilt: Ob ein Gut gewöhnlich oder
Giffen ist, kann von der betrachteten Budgetsituation
abhängen.
61 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Gut 1 ist gewöhnlich: Bei einem Anstieg des Preis von Gut 1
(Drehung der Budgetgeraden im Uhrzeigersinn) fällt die
nachgefragte Menge von Gut 1.
62 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Gut 1 ist Giffen: Bei einem Anstieg des Preis von Gut 1
(Drehung der Budgetgeraden im Uhrzeigersinn) steigt die
nachgefragte Menge von Gut 1.
63 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Definition (Substitute und Komplemente)
Gut i heisst Substitut für Gut j 6= i, wenn die nachgefragte
Menge von Gut i bei einem Anstieg des Preises von Gut j
zunimmt: εi j (p, m) > 0.
Gut i heisst Komplement für Gut j, wenn die nachgefragte
Menge von Gut i bei einem Anstieg des Preises von Gut
j 6= i abnimmt: εi j (p, m) < 0.
In den beiden vorhergehenden Grafiken ist Gut 2 jeweils
ein Komplement für Gut 1.
64 / 99
2.9 Die Nachfragefunktion eines Konsumenten
Beispiel: Nachfragefunktion zu der
Cobb-Douglas-Nutzenfunktion u(x1 , x2 ) = x1a x21−a ist
f1 (p1 , p2 , m) = a
m
m
und f2 (p1 , p2 , m) = (1 − a) .
p1
p2
Einkommenselastizitäten sind ξ1 (p, m) = ξ2 (p, m) = 1:
Beide Güter sind normal.
Ausgabenanteile sind konstant: θ1 (p, m) = a bzw.
θ2 (p, m) = (1 − a).
Eigenpreiselastizitäten sind ε11 (p, m) = ε22 (p, m) = −1:
Beide Güter sind gewöhnlich.
Kreuzpreiselastizitäten sind ε12 (p, m) = ε21 (p, m) = 0: Die
Güter sind weder Komplemente noch Substitute für
einander.
65 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Fragestellung
Welche Eigenschaften muss die Nachfragefunktion eines
Konsumenten mit artiger Präferenzrelation besitzen?
Definition (Artige Nachfragefunktion)
Eine Nachfragefunktion f heisst artig, wenn für alle p > 0 und
m > 0 das Güterbündel f (p, m) das eindeutige optimale
Güterbündel in der Budgetmenge B(p, m) eines Konsumentens
mit artiger Präferenzrelation (bzw. Nutzenfunktion) ist.
66 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Satz (Budgetidentität)
Eine artige Nachfragefunktion erfüllt die Budgetidentität: Für
alle (p, m) > 0 gilt:
p1 f1 (p, m) + p2 f2 (p, m) = m
und damit
θ1 (p, m)ξ1 (p, m) + θ2 (p, m)ξ2 (p, m) = 1.
Die Budgetidentität folgt daraus, dass das optimale
Güterbündel bei einer monotonen Präferenzrelation stets
auf der Budgetgeraden liegt.
Anwendungsbeispiel: Es ist unmöglich, dass alle Güter
inferior sind.
67 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Satz (Homogenität vom Grad Null)
Eine artige Nachfragefunktion ist homogen vom Grad Null in
Preisen und Budget: Für alle (p, m) > 0 gilt
fi (t p,tm) = fi (p, m) für alle t > 0
und damit
εi1 (p, m) + εi2 (p, m) + ξi (p, m) = 0.
Dieser Satz gilt, da die Budgetmenge - und somit auch die
Lösung des Konsumentenproblems - unverändert bleibt,
wenn alle Preise und das Budget um den gleichen
Prozentsatz ändern.
Anwendungsbeispiel: Ist Gut 1 gewöhnlich und inferior, so
muss es ein Substitut für Gut 2 sein.
68 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Satz (Negativer Substitutionseffekt)
Für eine artige Nachfragefunktion gilt, dass die
Substitutionselastizität negativ ist:
εii∗ (p, m) := εii (p, m) + θi (p, m)ξi (p, m) ≤ 0.
Der Ausdruck εii (p, m) + θi (p, m)ξi (p, m) beschreibt die
Änderung der Nachfrage von Gut i wenn der Preis von Gut i
steigt und zugleich das Einkommen des Konsumenten so
erhöht wird, dass er sich das Güterbündel f (p, m) weiterhin
leisten kann.
In Reaktion auf eine solche einkommenskompensierte
Preiserhöhung von Gut 1 muss die nachgefragte Menge von
Gut 1 fallen, da ansonsten ein Widerspruch zu der Annahme
resultiert, dass f (p, m) das Nutzenmaximierungsproblem in
der Ausgangssituation löst.
69 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Das Güterbündel f (p, m) wurde in der Ausgangssituation (rote
Budgetgerade) gewählt und wird daher allen Güterbündeln
streng vorgezogen, die unterhalb der roten Budgetgeraden
liegen. Bei einer einkommenskompensierten Preiserhöhung
von Gut 1 (blaue Budgetgerade) muss also ein Güterbündel
gewählt werden, welches “links oberhalb” von f (p, m) auf der
blauen Budgetgeraden liegt.
70 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Konsequenzen des negativen Substitutionseffekt:
Normale Güter sind gewöhnlich.
Giffen-Güter sind inferior.
Im hier betrachteten Zwei-Güterfall gilt zudem:
Ist Gut i inferior, so ist es ein Substitut für Gut j.
Ist Gut i ein Komplement zu Gut j, so ist Gut i normal.
71 / 99
2.10 Eigenschaften artiger Nachfragefunktionen
Beachte:
Die Gleichung εii∗ (p, m) = εii (p, m) + θi (p, m)ξi (p, m) wird oft
als
εii (p, m) = εii∗ (p, m) + (−θi (p, m)ξi (p, m))
geschrieben und als
Gesamteffekt = Substitutionseffekt + Einkommenseffekt
interpretiert.
Der Substitutionseffekt ist im Lehrbuch anders als hier
definiert - im Ergebnis macht dies aber keinen
Unterschied.
72 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Analog zu dem Nutzenmaximierungsproblem
max u(x1 , x2 ) unter der NB p1 x1 + p2 x2 ≤ m
x1 ,x2
kann man das Ausgabenminimierungsproblem
min p1 x1 + p2 x2 unter der NB u(x1 , x2 ) ≥ ū
x1 ,x2
definieren.
Die Lösung des Ausgabenminimierungsproblems
x = h(p, ū) bezeichnet man als die kompensierte
Nachfragefunktion.
Zur besseren Unterscheidung bezeichnen wir die Lösung
des Nutzenmaximierungsproblems x = f (p, m) im
Folgenden als unkompensierte Nachfragefunktion.
73 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Die Ausgabenfunktion gibt das minimale Budget an,
welches es erlaubt, das Nutzenniveau ū bei den Preisen
p = (p1 , p2 ) zu erreichen:
E(p, ū) = p1 h1 (p, ū) + p2 h2 (p, ū).
Das entsprechende Gegenstück im
Nutzenmaximierungsproblem heisst indirekte
Nutzenfunktion:
U(p, m) = u( f1 (p, m), f2 (p, m)).
Für artige Nutzenfunktionen besteht ein enger
Zusammenhang zwischen den Lösungen des
Nutzenmaximierungs- und des
Ausgabenminimierungsproblems - man spricht von einer
Dualität.
74 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Ausgabenminimierung: h(p, ū) ist das billigste Güterbündel,
welches es ermöglich, das Nutzenniveau ū zu erreichen. Die
erforderlichen Ausgaben E(p, ū) können über die
Achsenabschnitte der entsprechenden Budgetgerade bestimmt
werden.
75 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
E(p,U(p, m)) = m, bzw. U(p, E(p, ū)) = ū: Für gegebene
Preise sind Ausgabenfunktion und indirekte
Nutzenfunktion invers zueinander.
h(p,U(p, m)) = f (p, m) bzw. h(p, ū) = f (p, E(p, ū)): Für
gegebene Preise stimmen kompensierte und
unkompensierte Nachfrage überein, wenn ū = U(p, m) bzw.
m = E(p, ū) gilt.
Diese Zusammenhänge implizieren, dass man
Ausgabenfunktion und kompensierte Nachfragefunktion
aus der Lösung des Nutzenmaximierungsproblems direkt
bestimmen kann.
76 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Beispiel: Cobb-Douglas-Nutzenfunktion u(x1 , x2 ) = x1a x21−a .
Nachfragefunktion ist f1 (p, m) = am/p1 und
f2 (p, m) = (1 − a)m/p2 .
Indirekte Nutzenfunktion ist daher:
a a (1 − a)m 1−a
a
1 − a 1−a
am
=m
.
U(p, m) = u( f (p, m)) =
p1
p2
p1
p2
Auflösen der Gleichung U(p, m) = ū nach m = E(p, ū) liefert die
Ausgabenfunktion:
E(p, ū) = ū
p a p 1−a
1
2
.
a
1−a
Einsetzen der Ausgabenfunktion in die unkompensierte
Nachfragefunktion liefert die kompensierte Nachfragefunktion:
h1 (p, ū) = ū
a p2
1 − a p1
1−a
, h2 (p, ū) = ū
1 − a p1
a p2
a
.
77 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Satz (Shepards Lemma)
Sie u eine artige Nutzenfunktion. Dann ist die kompensierte
Nachfragefunktion von Gut i gleich der partiellen Ableitung der
Ausgabenfunktion nach pi :
∂ E(p, ū)
= hi (p, ū).
∂ pi
Intuition:
Steigt pi um eine Einheit, so ermöglicht es das zusätzliche
Einkommen hi (p, ū) gerade weiterhin das Güterbündel
h(p, ū) zu konsumieren und somit das Nutzenniveau ū zu
erreichen.
78 / 99
2.11 Ausgabenfunktion und kompensierte Nachfrage
Satz (Kompensierte Nachfrage und
Substitutionselastizität)
Die Eigenpreiselastizität der kompensierten Nachfragefunktion
ist gleich der Substitutionselastizität der unkompensierten
Nachfragefunktion:
∂ hi (p, ū) pi
= εii∗ (p, E(p, ū))
∂ pi hi (p, ū)
Intuition: Die Substitutionselastizität beschreibt die Auswirkung
einer kompensierten Preisänderung - die genaue Form der
Kompensation (Bisher gewähltes Güterbündel erschwinglich
oder bisherigen Nutzenniveau erschwinglich) macht bei der
Bestimmung der Ableitungen keinen Unterschied.
79 / 99
2.12 Kompensierende und äquivalente Variation
Fragestellung
Der Preis von Gut 1 steigt von p1 auf p∗1 , während p2 und m
unverändert bleiben. Wie kann man die Auswirkung auf die
Wohlfahrt des Konsumenten quantifizieren?
Die Betrachtung der resultierenden Nutzenänderung
U(p∗1 , p2 , m) −U(p1 , p2 , m) liefert keine sinnvolle Antwort, da
die Grösse dieses Betrages davon abhängt, welche
Nutzenfunktion zur Darstellung einer Präferenzrelation
verwendet wurde.
Immerhin gibt jedoch das Vorzeichen der Differenz
U(p∗1 , p2 , m) −U(p1 , p2 , m) Auskunft darüber, ob der
Konsument sich verbessert oder verschlechtert.
80 / 99
2.12 Kompensierende und äquivalente Variation
Kompensierende Variation
Die kompensierende Variation gibt den Geldbetrag an, den der
Konsument nach der Preisänderung zusätzlich zu seinem Budget
erhalten muss, um das gleiche Nutzenniveau wie in der
Ausgangssituation zu erreichen:
CV = E(p∗1 , p2 , ū)) − m mit ū = U(p1 , p2 , m).
Da m = E(p1 , p2 , ū) gilt, kann dieses auch als
CV = E(p∗1 , p2 , ū)) − E(p1 , p2 , ū)
geschrieben werden.
Aus Shepards Lemma folgt dann:
CV =
Z p∗
1
p1
h1 ( p̃1 , p2 , ū)dtildep1 .
81 / 99
2.12 Kompensierende und äquivalente Variation
Äquivalente Variation
Die äquivalente Variation gibt den Geldbetrag an, der von dem
Budget des Konsumenten abgezogen werden kann, so dass sein
Nutzen um den gleichen Betrag wie durch die Preisänderung fällt:
EV = m − E(p1 , p2 , u∗ ) mit u∗ = U(p∗1 , p2 , m)
Da m = E(p∗1 , p2 , u∗ ) gilt, kann dieses auch als
EV = E(p∗1 , p2 , u∗ )) − E(p1 , p2 , u∗ )
Aus Shepards Lemma folgt dann:
EV =
Z p∗
1
p1
h1 ( p̃1 , p2 , u∗ )dtildep1 .
82 / 99
2.12 Kompensierende und äquivalente Variation
Kompensierende und äquivalente Variation wenn der Preis
von Gut 1 von p1 (rote durchgezogene Budgetgerade) auf p∗1
(blaue, durchgezogene Budgetgerade) steigt. Gut 2 ist hier
Numeraire, so dass die vertikalen Achsenabschnitte der
verschiedenen Budgetgeraden als Geldbeträge interpretiert
83 / 99
2.12 Kompensierende und äquivalente Variation
Beachte:
Kompensierende und äquivalente Variation hängen nur
von der zu Grunde liegenden Präferenzrelation, nicht aber
von der gewählten Nutzendarstellung, ab.
Kompensierende und äquivalente Variation stimmen im
allgemeinen (wie in der vorhergehenden Grafik) nicht
überein.
Eine Ausnahmefall sind die quasilinearen
Präferenzrelationen, da hier die Nachfrage von Gut 1 ist für
alle relevanten Budgetsituationen
einkommensunabhängig, so dass unkompensierte und
kompensierte Nachfrage von Gut 1 übereinstimmen:
f1 (p, m) = h1 (p, ū) = h1 (p, u∗ ).
84 / 99
2.12 Kompensierende und äquivalente Variation
Satz
Sei u eine artige quasilineare Nutzenfunktion. Dann gilt:
CV = EV =
Z p∗
1
p1
f1 ( p̃1 , p2 , m)d p̃1 .
R p∗
f1 ( p̃1 , p2 , m)d p̃1 ist die Fläche links von der
unkompensierten Nachfragefunktion von Gut 1, die
zwischen den Preisen p1 und p∗1 liegt. Diese Fläche wird
oftmals (so auch im Lehrbuch) als Änderung der
Konsumentenrente bezeichnet.
1
p1
85 / 99
2.12 Kompensierende und äquivalente Variation
Kompensierende und äquivalente Variation bei
quasilinearen Präferenzen als Fläche links von der
Nachfragefunktion zwischen den beiden Preisen. Beachte,
dass der Preis auf der vertikalen Achse abgetragen ist.
86 / 99
2.12 Kompensierende und äquivalente Variation
Im Allgemeinen, d.h. auch ohne die Annahme der
Quasilinearität, ist der Unterschied zwischen
kompensierender und äquivalenter Variation für kleine
Preisänderungen gering und beide Wohlfahrtsmasse
werden durch die Fläche links von der Nachfragefunktion
zwischen den beiden Preisen approximiert:
CV ≈ EV ≈
Z p∗
1
p1
f1 ( p̃1 , p2 , m)d p̃1
Diese Approximation ist um so besser, je kleiner der durch
−θ1 (p, m)ξ1 (p, m) beschriebene Einkommenseffekt ist.
Aus diesem Grund wird die Änderung der
Konsumentenrente oft als Wohlfahrtsmass einer
Preisänderung betrachtet.
87 / 99
2.13 Konsumentenrente
Betrachte einen Konsumenten mit artiger quasilinearer
Nutzenfunktion
u(x1 , x2 ) = v(x1 ) + x2 mit v(0) = 0, v0 (x1 ) > 0 und v00 (x2 ) < 0.
Gut 2 ist Numeraire: p2 = 1.
Dies erlaubt es, die Zahlungsbereitschaft v(x1 ) als
Geldbetrag zu interpretieren.
Definition (Konsumentenrente)
Die Differenz zwischen der Zahlungsbereitschaft v(x1 ) eines
Konsumenten und seinen Ausgaben z für Gut 1 heisst
Konsumentenrente:
kr = v(x1 ) − z.
88 / 99
2.13 Konsumentenrente
Die Konsumentenrente misst den Handelsgewinn des
Konsumenten
Ohne Handel von Gut 1 ist der Nutzen des Konsumenten
u(0, m) = m.
Der Nutzen des Konsumenten aus einem Handel, in dem er
x1 Einheiten von Gut 1 gegen Zahlung des Betrages z
erhält, ist u(x1 , m − z) = v(x1 ) + m − z.
Die Differenz v(x1 ) + m − z − m = v(x1 ) − z = kr ist der
Handelsgewinn.
R p∗
Frage: Was hat das mit dem Ausdruck
zu tun?
1
p1
f1 ( p̃1 , p2 , m)d p̃1
89 / 99
2.13 Konsumentenrente
Sei mit d(p1 ) := f1 (p1 , 1, m) die zum Preis p1 nachgefragte
Menge von Gut 1 bezeichnet. Die durch den Kauf dieser
Menge zum Preis p1 erzielte Konsumentenrente ist
kr(p1 ) = v(d(p1 )) − p1 d(p1 ).
Satz
kr(p1 ) =
R∞
p1 d1 ( p̃1 )d p̃1
Insbesondere gilt also
kr(p1 ) − kr(p∗1 ) =
Z p∗
1
p1
d( p̃1 )d p̃1 ,
so dass die zuvor als Änderung der Konsumentenrente
bezeichnete Fläche tatsächlich den Verlust an
Konsumentenrente darstellt, der durch einen Anstieg des
Preises von p1 auf p∗1 entsteht.
90 / 99
2.13 Konsumentenrente
Die Konsumentenrente bei Preis p1 ist die Differenz zwischen
der Zahlungsbereitschaft v(d(p1 )) und der Zahlung z = p1 d(p1 )
für die nachgefragte Menge des Gutes. Die
Zahlungsbereitschaft entspricht der blau umrandeten Fläche;
die Zahlung entspricht der grün schraffierten Fläche.
91 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Durch einen Konsumentenpreisindex wird versucht, die
Veränderung der Kaufkraft einer Währung zu messen.
Dazu wird in der Schweiz (und vielen anderen Ländern)
ein Laspeyres-Preisindex verwendet:
Für ein Basisjahr wird ein Warenkorb festgelegt, der den
Konsum eines “typischen” Konsumenten beschreiben soll.
In dem Basisjahr und den Folgejahren werden die zum Kauf
dieses Warenkorbs erforderlichen Ausgaben festgestellt.
Auf dieser Grundlage wird dann errechnet, um wieviel
Prozent die zum Kauf des Warenkorbs erforderlichen
Ausgaben angestiegen sind.
92 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Abbildung: Das Siegel der Wirtschaftswissenschaftlichen Fakultät der
Universität Basel zeigt Etienne Laspeyres (1834-1913), der von 1864
- 1866 Professor an der Universität Basel war.
93 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Frage
Was kann über die Wohlfahrt eines Konsumenten ausgesagt
werden, der im Basisjahr den Warenkorb konsumiert und
dessen Einkommen für ein Folgejahr entsprechend des
Konsumentenpreisindex angepasst wird?
Antwort
Der Konsument erzielt im Folgejahr ein höheres Nutzenniveau,
es geht ihm also besser.
94 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Begründung der Antwort:
Unterstelle eine artige Nutzenfunktion mit innerer Lösung des
Konsumentenproblems.
Der Kaufkraftausgleich ermöglicht es dem Konsumenten das
im Basisjahr gewählte Güterbündel weiterhin zu konsumieren
- er kann sich durch den Inflationsausgleich also nicht
verschlechtern.
Gibt es eine Änderung der relativen Preise, wird der
Konsument im Folgejahr jedoch ein anderes Güterbündel
wählen - dieses Güterbündel wird dem im Basisjahr gewählten
Güterbündel streng vorgezogen.
Schlussfolgerung:
Die durch den Kaufpreisindex gemessene Inflationsrate ist
systematisch verzerrt: sie überschätzt den tatsächlichen
Kaufkraftverlust.
Die “korrekte” Inflationsrate könnte prinzipiell mit der
kompensierende Variation bestimmt werden.
95 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Modellrahmen:
Betrachte Gut 2 als Numeraire und setze p2 = 1.
Gehe davon aus, dass der Preis p1 von Gut 1 in einer
Situation ohne Besteuerung dem Wettbewerbspreis
entspricht.
Unterstelle, dass das Angebot von Gut 1 vollkommen
elastisch ist, so dass eine Mengensteuer auf Gut 1 mit
Satz t den Preis des Gutes von p1 auf p1 + t ändert.
Betrachte die Auswirkung der Einführung eine
Mengensteuer mit gegebenem Satz t > 0.
96 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Auswirkung einer Mengensteuer: Nach Einführung der
Mengensteuer mit Satz t wird (x1∗ , x2∗ ) nachgefragt; die
Steuereinnahmen tx1∗ entsprechen der Länge der rot markierten
Strecke auf der Achse für Gut 2.
97 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Ist Gut 1 gewöhnlich, so führt die Einführung einer
Mengensteuer dazu, dass die nachgefragte Menge von
Gut 1 fällt.
Fragt der Konsument nach Einführung der Mengensteuer
das Güterbündel (x1∗ , x2∗ ) nach, so sind die
Steuereinnahmen tx1∗ .
Nach Einführung der Mengensteuer geht es dem
Konsumenten offenkundig schlechter als in der
Ausgangssituation: U(p1 + t, 1, m) < U(p1 , 1, m).
Würde die Mengensteuer durch eine Kopfsteuer ersetzt,
die zu den gleichen Steuereinnahmen führt, so würde es
dem Konsumenten besser als in der Situation mit
Mengensteuer gehen:
U(p1 + t, 1, m) < U(p1 , 1, m − tx1∗ ).
98 / 99
2.13 Beispiele zur Wohlfahrtsanalyse
Vergleich von Mengen- und Kopfsteuer: Führen Mengensteuer
und Kopfsteuer zu den gleichen Steuereinnahmen in Höhe von tx1∗ ,
so zieht der Konsument die Kopfsteuer vor.
99 / 99