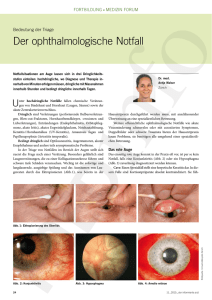
Vortrag: Beschreibende Statistik

Stochastik in der Schule:
Globale Ideen, lokale Bedeutungen, zentrale Tätigkeiten
von
Bernhard Kröpfl, Werner Peschek und Edith Schneider, Klagenfurt
Kurzfassung: In der vorliegenden Arbeit werden globale Ideen, lokale Bedeutungen und zentrale Tätigkeiten
der Stochastik herausgearbeitet und damit didaktische Orientierungen für die Planung, Entwicklung, Durchführung und Bewertung des Stochastikunterrichts angeboten. Curriculare Umsetzungen und Konkretisierungen
dieser Überlegungen findet man in (Kronfellner/Peschek 1998), einem Lehrbuch für die S II, sowie in (Kröpfl u.
a. 1999), einem Lehrbuch für die statistische Grundausbildung von Betriebswirtschaftler/inne/n.
Abstract: In this paper global ideas, local meanings and central actions of stochastic are worked out and with
that didactical orientations for the designing, development, realisation and evaluation of the teaching of stochastic
are offered. One finds curricular realisations and concretizations of these considerations in (Kronfellner/Peschek
1998), a textbook for the S II as well as in (Kröpfl u. a. 1999), a textbook for the statistical basic training of
economic students.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 1
1
Beschreibende Statistik
Es ist weitgehend unbestritten, dass die beschreibende Statistik in vielen gesellschaftlichen
Lebensbereichen angewandt wird, in den Wissenschaften ebenso wie in der Wirtschaft und
Technik, in der Politik, im Sport und in vielen kulturellen Bereichen; die Ergebnisse statistischer Erhebungen begegnen uns nicht nur in Fachzeitschriften, sondern fast täglich auch in
Zeitungen und Journalen, im Radio und im Fernsehen, in politischen Argumentationen wie in
Festtagsreden, auf Werbeplakaten wie auch in amtlichen Formularen oder Bescheiden. Die
Bedeutung der beschreibenden Statistik in vielen beruflichen und außerberuflichen
Lebenssituationen (auch von Schülern/innen) ist ein Argument, das für eine unterrichtliche
Behandlung dieses mathematischen Gebiets spricht.
Manchem/r Lehrer/in erscheint die beschreibende Statistik jedoch als zu einfach und elementar, um im Mathematikunterricht (der Sekundarstufe II) sinnvoll behandelt werden zu können.
Tatsächlich beschränken sich die rechentechnischen Anforderungen im Wesentlichen auf das
Rechnen mit Prozenten, Brüchen, Quadraten, Wurzeln, Betrags- und Summenzeichen, lediglich in der zweidimensionalen Statistik trifft man bei der Herleitung der Regressionsgleichung
auf „höhere Mathematik“.
Andere Lehrer/innen hingegen sind der Auffassung, dass die beschreibende Statistik sehr hohe
Anforderungen hinsichtlich Kontextverständnis, Darstellung und Interpretation stelle und aus
diesem Grund für den Schulunterricht eher zu anspruchsvoll sei. Tatsächlich ist die beschreibende Statistik allein innermathematisch kaum angemessen behandelbar; außermathematische
Sachverhalte erfordern aber nicht selten weiterreichendes Kontextwissen und -verständnis
(und ein gewisses Maß an Motivation, sich mit solchen Problemstellungen zu befassen) sowie
einen kritischen Umgang mit Darstellungen und Interpretationen der kontextbezogenen Daten.
Beide Standpunkte führen zur selben Konsequenz: einer in vielen Fällen eher stiefmütterlichen und oft auch recht unangemessenen unterrichtlichen Behandlung der beschreibenden
Statistik.
Folgt man der Sichtweise von R. Fischer und G. Malle (1985, S. 221), wonach sich Mathematik „im Wechselspiel zwischen Darstellen, Interpretieren und Operieren“ vollzieht, wie
auch ihrem (vielfach bestätigten) Befund, dass das Operative den traditionellen Mathematikunterricht so stark beherrscht, dass (zu) wenig Raum für das Darstellen und Interpretieren
bleibt, dann kommt zur o. a. Praxisrelevanz ein weiteres Argument für die unterrichtliche
Behandlung der beschreibenden Statistik hinzu: die Chance, dem Darstellungs- und
Interpretationsaspekts im Mathematikunterricht einen angemesseneren Stellenwert
einzuräumen.
In dem im Folgenden skizzierten Konzept einer (klassischen) beschreibenden Statistik (vgl.
auch Peschek 1998) kommt dem Darstellungs- und Interpretationsaspekt jedenfalls zentrale
Bedeutung zu.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 2
1. 1
Beschreibende Statistik im Spannungsfeld zweier globaler Ideen
Für die beschreibende Statistik lassen sich mindestens zwei globale („fundamentale“) Ideen
identifizieren, die die Entwicklung dieses Gebiets nachhaltig beeinflusst haben und ihr
heutiges Erscheinungsbild prägen: Die Idee der Mustererkennung und -darstellung sowie die
Idee der Raffung.
Viele statistische Tätigkeiten und Arbeitsweisen (insbesondere diverse Verfahren der grafischen und halbgrafischen Darstellung) zielen darauf ab, in großen Datensätzen explorativ
globale Muster (Strukturen, Verläufe, Beziehungen) zu erkennen, diese sichtbar zu machen
und zu beschreiben (darzustellen). Abb. 1 etwa macht die starken Geburtenrückgänge seit
1970 wie jene der (Nach-)Kriegsjahre ebenso erkenn- und sichtbar wie den Frauenüberschuss
in den älteren Jahrgängen u. v. a. m., in Abb. 2 wird es wohl darum gehen, die starken saisonalen Schwankungen in der Energieaufbringung Klagenfurts (bei leicht steigender Gesamtentwicklung) zu erkennen bzw. deutlich zu machen.
Abb. 1: Alterspyramide für Österreich
Energieaufbringung (in Mio. kWh)
160
140
120
100
80
Zeitraum t
60
0
2
4
6
8
10
12
14
16
Abb. 2: Energieaufbringung in Klagenfurt 1990 - 1993
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 3
Der Raffung als weiterer globaler Idee der beschreibenden Statistik liegt eine grundlegende
menschliche und gesellschaftlich höchst bedeutsame Denkstrategie zugrunde: Wer umfangreiche, komplexe Informationen (Datensätze) vergleichen will oder muss, wer angesichts
unübersichtlicher Informationslage Entscheidungskriterien sucht, kann versuchen, sich durch
operative Komprimierung der Daten Überblick, Vergleichsmöglichkeiten oder intersubjektiv
nachvollziehbare Entscheidungsgrundlagen zu schaffen: Addition und deren Kommutativität
ermöglichen es uns, die in einem Restaurant konsumierten Speisen und Getränke mit einem
Gesamtbetrag zu bewerten und zu bezahlen, die verschiedenen Noten im Verlauf eines
Schuljahres werden zu einer Endnote (mit entsprechenden Konsequenzen) verdichtet, das
quantitative Verhältnis zwischen Budgetdefizit (selbst Produkt einer extremen Raffung) und
Bruttonationalprodukt (ebenfalls eine extreme Raffung) macht uns für den Euro (un-)tauglich
usw. Erst solche Raffungen machen die Mathematik - in unserem Fall die Statistik - so
„einfach, klar und undurchsichtig“, wie dies R. Fischer (1986, S. 123) einmal formuliert hat.
In der beschreibenden Statistik finden wir die Idee der Raffung fast durchgängig, beginnend
bei der Datenerhebung (Zusammenfassung in Gruppen) über die Klasseneinteilung und das
Histogramm bis hin zu - und ganz besonders bei - den Zentral- und Streuungsmaßen; der
damit erreichbaren Vereinfachung und Übersichtlichkeit steht das Problem der Reduktion und
geringeren Transparenz gegenüber.
Wesentlichstes Anliegen der Raffung ist Gewinn an Übersicht. Damit unterstützt die Raffung
einerseits die Mustererkennung (globaler Überblick über Verläufe, Trends, globale Auffälligkeiten), läuft ihr andrerseits aber auch zuwider, denn der Raffung ist im Prozess der Komprimierung ja praktisch keine Grenze gesetzt: die Raffung hat ihr Ziel dann am besten erreicht,
wenn es gelingt, alle Daten auf ein zentrales Moment, eine einzige Kennzahl, ein einziges
grafisches Symbol zu reduzieren. Eine solche Verdichtung der Information ist jedoch i. A. mit
Verlust an Information verbunden, d. h., Gewinn an Übersicht bedeutet meist auch Verlust an
Information. Abb. 3 soll diesen Zusammenhang veranschaulichen:
Abb. 3: Überblick vs. Informationsgehalt bei der Raffung
In der Praxis sollte das subjektive und zweckabhängige Bedürfnis nach Mustererkennung dem
Prozess der Raffung dort Einhalt gebieten, wo ausreichend Überblick erreicht ist, die
wesentlichen (Einzel-)Informationen und Strukturen aber noch erkennbar sind (vgl. Abschnitt
1. 2, Abb. 7 - 9, sowie Abschnitt 1. 3).
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 4
1. 2
Zentrale Tätigkeiten und lokale Deutungen
in der eindimensionalen beschreibenden Statistik
Neben einer geeigneten Datenerhebung (mit ihrer ganzen Problematik), auf die hier nicht
näher eingegangen wird, gehören die Darstellung der Daten sowie die Ermittlung von
statistischen Kennzahlen (Zentral- und Streuungsmaße, Schiefe u. a.) zu den zentralen
Tätigkeiten der eindimensionalen beschreibenden Statistik.
Die Darstellung statistischer Daten lässt sich in Form von Tabellen meist besonders einfach
und platzsparend realisieren. Andrerseits sind Tabellen manchmal aber auch etwas unübersichtlich, man muss sich oft erst „einlesen“ und man kann Größenvergleiche nur über die angegebenen Zahlenwerte durchführen. Grafische Darstellungen hingegen zielen darauf ab,
einen raschen Überblick zu ermöglichen, Größenverhältnisse und Muster rasch zu erkennen.
Im Vergleich zu tabellarischen Darstellungen sind sie meist aufwendiger zu erstellen, benötigen mehr Platz und sind anfälliger für Missverständnisse und gegenüber Fehlinterpretationen.
Bei der Behandlung der Grundtypen grafischer Darstellungen (vor allem Stab-, Kreis- und
Streifendiagramm, Piktogramm, Liniendiagramm) sind deren Vor- und Nachteile (lokale
Bedeutungen) mitzubedenken: Stabdiagramme etwa ermöglichen sehr viel einfacher als Kreisdiagramme sichere Größenvergleiche zwischen zwei Werten, letztere wiederum stellen den
Anteil der einzelnen Werte an der Gesamtheit dar und begünstigen so u. a. den Vergleich
zwischen zwei Gruppen von Werten:
15
Tabak
Hi
Öl
10
Chemie
Elektro
5
Tabak
Öl
Metall
Nahrungsmittel
Fahrzeuge
Chemie
0
Elektro
Nahrungsmittel
Metall
Fahrzeuge
Abb 4: Häufigkeitsverteilung der Variablen „Branche“ für 35 Industrieunternehmen als Stabund als Kreisdiagramm
Aus dem Stabdiadramm in Abb. 4 erkennt man schneller als aus dem Kreisdiagramm, dass die
Anzahl der Elektrounternehmen größer ist als die Anzahl der Ölunternehmen, aus dem Kreisdiagramm wiederum ist sehr viel einfacher zu erkennen, dass der Anteil der Elektro-, Öl- und
Nahrungsmittelunternehmen zusammen größer ist als der aller anderen Unternehmen.
Die Liniendiagramme in Abb. 5 und Abb. 6 stellen thematisch sehr ähnliche Zeitreihen dar und sind doch sehr unterschiedlich zu interpretieren: Während das Liniendiagramm in Abb. 5
Bestandsdaten darstellt, die zu bestimmten Zeitpunkten erhoben wurden, handelt es sich bei
den in Abb. 6 dargestellten Daten um Bewegungsdaten, die jeweils für einen bestimmten
Zeitraum ermittelt wurden. Das hat Konsequenzen: Während die Verbindungslinien in Abb. 5
einigermaßen sinnvoll interpretiert werden können (sofern man eine gleichmäßige
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 5
100
Geburten (in Tsd.)
Bevölkerung (in Mio.)
Entwicklung zwischen den gemessenen Werten unterstellt), ist eine entsprechende
Interpretation der Verbindungslinien in Abb. 6 nicht möglich (die Darstellung dieser Zeitreihe
in einem Stabdiagramm würde allfälligen Fehlinterpretationen besser vorbeugen).
90
80
70
60
1000
900
800
700
600
50
500
40
400
30
300
20
200
100
10
Jahr
0
50
60
70
80
Jahr
0
85
90
Abb. 5: Bevölkerungsentwicklung
in Deutschland
86
87
88
89
90
91
Abb. 6: Entwicklung der Geburtenzahlen
in Deutschland
Das Wechselspiel von Raffung und Mustererkennung wird gerade auch bei grafischen
Darstellungen recht deutlich: Die Darstellung der Beschäftigtenzahlen in Abb. 7 ist unübersichtlich und lässt für die Häufigkeitsverteilung wenig „Struktur“ erkennen. Verzichtet man
auf die Unterscheidung nahe beieinander liegender Werte und fasst benachbarte Werte zu
einer Klasse zusammen (Raffung!), so erhält man z. B. die in Abb. 8 gezeigte, in mancher
Hinsicht weit aufschlussreichere Darstellung.
2
Hi
1
756.300
407.169
402.000
379.252
344.553
332.700
309.757
298.000
287.957
284.000
265.566
240.000
214.399
210.848
201.139
187.377
179.332
166.000
162.000
159.100
156.800
147.195
138.326
133.000
130.745
126.500
111.900
102.423
86.900
101.000
85.500
67.500
55.123
40.181
0
Beschäftigte
Abb. 7: Beschäftigtenzahlen in 35 Industrieunternehmen
Hi
16
14
12
10
8
6
4
2
0
0
200
400
600
800
Beschäftigte (in Tsd.)
Abb. 8: Beschäftigtenzahlen in 35 Industrieunternehmen
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 6
Natürlich hätte man die Raffung auch sehr viel weiter treiben, die Klassenbreiten auf 200.000,
300.000 oder gar 800.000 vergrößern können. Das Ergebnis wäre dann zwar noch übersichtlicher als in Abb. 8, allerdings wäre der Informationsgehalt nur noch sehr gering. Insbesondere würde man durch eine so extreme Raffung fast alles an (Einzel-)Information verlieren
und die „Struktur“ der Verteilung völlig zerstören (vgl. Abb. 9). Die Frage nach einer
sinnvollen Klasseneinteilung (Raffung) ist somit eine sehr wesentliche.
40
Hi
30
20
10
0
0
200000
400000
600000
800000
1000000
Beschäftigte
Abb. 9: Beschäftigtenzahlen in 35 Industrieunternehmen
Fast täglich stößt man auf Grafiken, die nicht sosehr statistische Daten als vielmehr ein grobes
Unverständnis für die Zielsetzungen und die Bedeutung grafischer Darstellungen erkennen
lassen; Abb. 10 und Abb. 11 mögen hier als - nicht weiter kommentierte - Beispiele unzweckmäßiger bis unsinniger grafischer Darstellungen statistischer Daten dienen.
Abb. 10
Abb. 11
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 7
Schon bei einfachen Grafiken ist man mit grundlegenden Problemen der grafischen
Darstellung von statistischen Daten und verschiedenen Manipulationsmöglichkeiten
konfrontiert. In den beiden folgenden Beispielen soll dies zumindest exemplarisch gezeigt
werden, wobei in Beispiel 1 allein durch verschiedene Festlegungen der Achseneinheiten (gibt
es eine „richtige“?), in Beispiel 2 mit verschiedenen Klasseneinteilungen und Bezugsbasen
„manipuliert“ wird.
Beispiel 1: Besucher/innenzahlen im Strandbad Klagenfurt:
Jahr
Besucher/innen
Opposition:
1970
1972
1976
1978
1981
755.000
815.000
845.000
840.000
945.000
Es ist ein Skandal: Die Besucher/innenzahlen im Strandbad explodieren und
die Stadtregierung weigert sich nach wie vor, finanzielle Mittel für den Ausbau
des Strandbades bereitzustellen!
950000
Besucher/innenzahl
900000
850000
800000
750000
700000
1968
1973
1978
1983
Jahr
Abb. 12a
Besucher/innenzahl
Stadtregierung: Die Entwicklung der Besucher/innenzahlen im Strandbad ist uns wohlbekannt, wir können daraus aber keinen derartigen Zuwachs erkennen, der die
Finanzierung einer Erweiterung des Strandbades rechtfertigen würde!
800000
600000
400000
200000
0
1968
1970
1972
1974
1976
1978
1980
1982
Jahr
Abb. 12b
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 8
Beispiel 2: An einer politischen Diskussionsveranstaltung nahmen 140 Personen teil. Die
Altersverteilung der Teilnehmer/innen an dieser Veranstaltung ist aus Abb. 13a - d ersichtlich:
Hi
50
40
30
20
10
0
15-19
20-29
30-44
45-69
Alter
Abb. 13a: Das Interesse an der Politik steigt mit zunehmendem Alter!
Hi/Jahrgang
5
4
3
2
Alter
45-69
30-44
15-19
0
20-29
1
Abb. 13b: Das Interesse an der Politik sinkt mit zunehmendem Alter!
Hi/Jahrgang
5
Hi
80
4
70
60
3
50
40
2
30
1
20
10
0
0
15-24
25-39
40-69
15-24
25-39
40-69
Alter
Alter
Abb. 13c: Gleichgültig, ob man nach der in Abb. 13a oder nach der in Abb. 13b gewählten
Methode vorgeht, in jedem Fall ist es die mittlere Generation, die sich am wenigsten für Politik interessiert!
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 9
hi
6
5
4
3
2
1
0
15-19
20-29
30-44
45-69
Alter
Abb. 13d: Bezogen auf die Altersverteilung in dieser Kleinstadt zeigten alle Altersgruppen
ungefähr gleich großes Interesse bzw. Desinteresse an dieser Veranstaltung!
Mit statistischen Kennzahlen versucht man, bestimmte Aspekte statistischer Daten durch ein
einziges Datum zu beschreiben.
So etwa ist das wesentliche Anliegen der Zentralmaße, ihre lokale Bedeutung, darin zu sehen,
dass eine ganze (oft unübersichtliche) Liste von Daten durch einen einzigen,
„repräsentativen“, „durchschnittlichen“ oder „typischen“ Wert ersetzt wird. Dieser Wert soll
die gesamte Liste der Daten möglichst gut charakterisieren und so auch verschiedene Listen
von Daten vergleichbar machen. Natürlich stellt eine derartige Komprimierung vieler Daten in
ein einziges Zentralmaß eine sehr extreme Raffung dar, bei der viele (oft sehr wichtige)
Einzelinformationen verlorengehen; die beschreibende Statistik kennt für diese Art der
Raffung verschiedene Modelle (diverse Mittelwerte, Median, Modus). Didaktisch und im
Hinblick auf Anwendungen sind dabei weniger die jeweiligen Berechnungsmethoden von
Interesse als vielmehr die lokalen Bedeutungen der einzelnen Modelle, ihre Aussagekraft und
Anwendbarkeit. Wenn ein Statistiker etwa sagt, dass die 100 Mitarbeiter/innen eines
Unternehmens „durchschnittlich“ Euro 2.000,-- pro Monat verdienen, so kann er damit
meinen, dass bei gleichmäßiger Verteilung der Summe aller Gehälter auf alle
Mitarbeiter/innen ein/e Mitarbeiter/in ungefähr Euro 2.000,-- monatlich bekommen würde
(arithmetisches Mittel), er kann damit aber auch meinen, dass 50 Mitarbeiter/innen höchstens
Euro 2.000,--, 50 Mitarbeiter/innen hingegen mindestens Euro 2.000,-- pro Monat verdienen
(Median). Denkbar wäre weiters auch die Interpretation, dass das am häufigsten ausbezahlte
Entgelt Euro 2.000,-- beträgt (Modus). Das Konzept des arithmetischen Mittels ist das der
Summenbildung (daher muss diese möglich und sinnvoll sein!) und der gleichmäßigen
Verteilung - in diesem Sinne ist es „egalitär“ -, es reagiert stark auf extreme Werte
(„Ausreißer“) und setzt metrische Daten voraus. Das Konzept des Medians besteht darin,
zwischen einer „besseren“ und einer „schlechteren“ Hälfte zu unterscheiden, es ist in diesem
Sinn „elitär“, darüber hinaus ausreißerunempfindlich (robust) und verlangt nur Ordinaldaten.
Das Konzept des Modus schließlich sucht nach einem häufigsten Wert, der aber wohl nur
dann als „typischer“ Wert akzeptabel erscheint, wenn er sehr viel häufiger auftritt als alle
anderen Werte; der Modus ist auch auf nominalskalierte Daten anwendbar.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 10
So simpel die Zentralmaße auf den ersten Blick erscheinen mögen, wenn man bedenkt, dass
selbst gesetzliche Bestimmungen (etwa Stipendiengesetze, Studienzulassungen) die Verwendung des arithmetischen Mittels für die Mittelung von (üblicherweise ordinalskalierten) Noten
zwingend vorschreiben und auch stoffdidaktische Analysen mit diesem Thema gewisse
Schwierigkeiten haben (siehe etwa Reichel, Hanisch und Müller 1987, S. 31), dann kann man
erahnen, dass die Interpretation der lokalen Bedeutungen mancher Zentralmaße schwieriger,
zugleich aber auch interessanter ist, als man zunächst angenommen hatte.
Durch die extreme Raffung, die zu den Zentralmaßen führt, gehen viele Informationen verloren, unter anderem auch Informationen darüber, wie gut das Zentralmaß die vorliegenden
Daten repräsentiert bzw. wie stark die Einzeldaten um das Zentralmaß streuen. (Würden Sie
etwa als Nichtschwimmer einen Teich durchwaten, von dem Sie lediglich wissen, dass er
„durchschnittlich“ 80 cm tief ist?) Im Hinblick auf solche Beurteilungen ist die Angabe eines
Zentralmaßes alleine völlig unzureichend, die Raffung zu extrem. Die beschreibende Statistik
versucht, diesen Informationsverlust durch Angabe eines Streuungsmaßes zu mildern.
Spannweite und Interquartilspannweite (Abstand zwischen oberer und unterer Quartile) sind
sehr einfache, anschauliche Streuungsmaße, die für die Anliegen der beschreibenden Statistik
meist völlig genügen, die mittlere absolute Abweichung (vom Median oder vom arithmetischen Mittel) als arithmetisches Mittel der Abstände („durchschnittlicher Abstand“)
modelliert recht gut die intuitive Vorstellung von „mittlerer Streuung“. Das in der
beschreibenden Statistik am häufigsten verwendete Streuungsmaß hingegen, die empirische
Standardabweichung, erweist sich als unanschaulich und schwer interpretierbar (Seitenlänge
des „durchschnittlichen Abstandsquadrats“, genauer: Seitenlänge jenes Quadrats, dessen
Flächeninhalt das arithmetische Mittel der Flächeninhalte all jener Quadrate repräsentiert, die
man erhält, wenn man den Abstand jedes einzelnen Werts vom arithmetischen Mittel als Seite
eines Quadrats versteht). Mit dieser, von intuitiven Vorstellungen sehr abgehobenen
Modellierung der Streuung läuft die empirische Standardabweichung den Anliegen der
beschreibenden Statistik (Gewinn an Einsicht und Überblick) geradezu zuwider und erscheint
daher für die beschreibende Statistik weniger geeignet; ihre eigentliche Bedeutung kommt erst
in der Wahrscheinlichkeitsrechnung und in der schließenden Statistik zum Tragen.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 11
1. 3
Zusammenspiel von Raffung und Mustererkennung - ein Beispiel
Die folgende Tabelle zeigt die Bruttoeinkommen (in ATS) von 50 Beschäftigten in 25 verschiedenen Wirtschaftsbereichen:
11.211
12.338
17.064
12.560
14.429
15.357
17.571
24.891
14.637
19.499
21.099
11.841
16.277
15.106
15.715
32.608 18.004 26.365 13.757 21.896 13.677 20.118
15.590 14.040 18.082 15.408 25.653 17.399 28.316
23.393 16.936 23.539 15.500 21.067 13.608 20.560
18.910 20.693 31.063 15.535 20.700 10.679 14.964
22.006 13.570 19.654 17.167 20.934 7.221 6.017
Das Kastenschaubild in Abb. 14 liefert für diese 50 Einkommen eine grafische Veranschaulichung von Median, unterer und oberer Quartile (und damit auch des Interquartilabstands)
sowie des höchsten und des niedrigstens Wertes (und damit der Spannweite): Das höchste
Einkommen liegt bei ca. ATS 32.500,--, das niedrigste bei ca. ATS 6.000,--, die (mittlere)
Hälfte der Beschäftigten verdient monatlich zwischen ca. ATS 14.500,-- und knapp ATS
20.500,--, der „Durchschnittsverdiener“ (im Sinne des Medians) kommt auf monatlich ca.
ATS 17.000,--. Es sind zwei extrem niedrige und drei vergleichsweise sehr hohe Einkommen
erkennbar, zwischen ca. ATS 10.500,-- und ca. ATS 26.500,-- darf man annehmen, dass die
Daten „dicht“ liegen (keine großen Lücken auftreten), wobei die Verteilung etwas
„rechtsschief“ ist (d. h., die Daten streuen bei den oberen Einkommen etwas stärker als in der
unteren Hälfte).
35000
30000
25000
20000
15000
10000
5000
0
Abb. 14: Bruttoeinkommen von 50 Beschäftigten (in ATS)
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 12
Aus diesen stark gerafften Daten (Zentral- und Streuungsmaße) lässt sich also schon sehr viel
über die Verteilung der Einkommen aussagen, allerdings ist aus den dargestellten Kennzahlen
(Raffung!) die Struktur der Verteilung nicht mehr erkennbar. Diese oft wichtige Information
kann z. B. recht gut einem Stängel-Blatt-Diagramm (halbgrafische Darstellung) entnommen
werden; im vorliegenden Beispiel könnte anhand des Stängel-Blatt-Diagramms in Abb. 15a
etwa auffallen, dass sich die Einkommen um ATS 15.000,-- wie auch bei ca. ATS 20.000,-häufen, somit eher eine zweigipfelige Verteilung vorliegt als eine Gauß´sche Glockenkurve.
Mehrgipfelige Verteilungen sind aber immer alamierend, sie verweisen auf eine mögliche
Inhomogenität der zugrundeliegenden Daten. So könnten etwa die zwei Gipfeln im StängelBlatt-Diagramm von Abb. 15a durch Einkommensunterschiede zwischen Arbeitern/innen und
Angestellten bedingt sein, oder auch durch Einkommensunterschiede zwischen Frauen und
Männern. Im Stängel-Blatt-Diagramm von Abb. 15b wurden die Einkommen von Frauen (fett,
kursiv) und Männern verschieden gekennzeichnet, das Ergebnis ist recht aufschlussreich!
Eine Konsequenz aus dem in Abb. 15a erkannten Muster (und dem in Abb. 15b erkannten,
möglichen Ursachen) könnte eine für die Einkommen von Frauen und Männern getrennte
(aber vergleichende) Darstellung relevanter Kennzahlen in zwei Kastenschaubildern sein
(Abb. 16).
Tausend Hundert
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Tausend
0
2
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
6
28
35
5667
0469
1345557
29
0135
009
46
05679
008
0
35
8
6
3
3
0
6
Abb. 15a: Bruttoeinkommen (in ATS)
PFL-Mathematik 2000-02, Seminar 2,
Hundert
0
2
6
28
35
5667
0469
1345557
29
0135
009
46
05679
008
0
35
8
6
3
3
0
6
fett, kursiv: Frauen
Abb. 15b: Bruttoeinkommen (in ATS)
„Stochastik in der Schule“ (Statement)
Seite 13
35000
30000
25000
20000
15000
10000
5000
Frauen
Männer
0
Abb. 16: Bruttoeinkommen von 25 Frauen und 25 Männern
Bei den in diesem Beispiel verwendeten Daten handelt es sich im übrigen um die Durchschnittseinkommen (im Sinne des Medians) aller weiblichen und männlichen Beschäftigten in
25 Wirtschaftsbereichen in Österreich im Jahre 1994.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 14
1. 4
Zweidimensionale beschreibende Statistik
Bei der eindimensionalen Betrachtung von Merkmalen gehen Zusammenhänge zwischen zwei
(oder mehreren) Merkmalen verloren, zum Beispiel mögliche Zusammenhänge zwischen den
jährlichen Umsätzen und den Beschäftigtenzahlen in verschiedenen Unternehmen. Methoden
zur Beschreibung von Zusammenhängen zwischen zwei Merkmalen liefert die zweidimensionale beschreibende Statistik. Dabei werden dieselben globalen Ideen und ähnliche lokale Bedeutungen bzw. zentrale Tätigkeiten wie in der eindimensionalen Statistik sichtbar:
Zunächst wird man die Ausprägungen der beiden Merkmale wohl tabellieren. Falls für beide
Merkmale metrische Daten vorliegen, kann man diese in einem Streudiagramm grafisch
darstellen (Abb. 17).
Umsatz (in Mrd. $)
140
120
100
80
60
40
20
0
0
200.000
400.000
600.000
800.000
Beschäftigte
Abb. 17: Beschäftigtenzahlen und Umsätze in 35 Industrieunternehmen
Anhand des Streudiagramms bzw. anhand der durch die eingezeichneten Punkte gegebenen
Punktwolke lässt sich ein gewisser (hier nicht sonderlich stark ausgeprägter) Trend dahingehend erkennen, dass Unternehmen mit höheren Beschäftigtenzahlen tendenziell auch höhere
Umsätze aufweisen. Dieser Trend in Abb. 17 lässt sich verdeutlichen und in den Vordergrund
rücken, wenn man ihn als Graph einer (im einfachsten Fall linearen) Funktion modelliert und
diesen Graphen im Streudiagramm einzeichnet. Die in Abb. 18 dargestellte Trendgerade
wurde „nach Gefühl“ eingezeichnet; sie ist für die vorliegenden zweidimensionalen Daten in
ähnlichem Sinn repräsentativ wie ein Zentralmaß für eine eindimensionale Liste von Daten.
Umsatz (in Mrd$)
140
Trendgerade
120
100
80
60
40
20
0
0
200.000
400.000
600.000
800.000
Beschäftigte
Abb. 18: Beschäftigtenzahlen und Umsätze in 35 Industrieunternehmen
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 15
Aus der Grafik lässt sich leicht eine Gleichung der Trendgeraden ermitteln, aus der dann entsprechende quantitative Aussagen ablesbar bzw. berechenbar werden.
Gefühle sind subjektiv und nicht normiert, daher kann es für die nach Gefühl gezeichnete
Trendgerade kein eindeutiges Ergebnis geben. Wer ein intersubjektiv eindeutiges Ergebnis
möchte oder braucht, wird den Trend daher nach einem genormten Verfahren, etwa der
Methode der kleinsten Quadrate, ermitteln und zum Beispiel durch eine Regressionsgerade
beschreiben. Je nachdem, ob man dabei die Abstandsquadrate der Punkte von der
Regressionsgeraden in vertikaler Richtung (1. Regressionsgerade) oder in horizontaler
Richtung (2. Regressionsgerade) minimiert, erhält man eine Gerade, die gegenüber der nach
Gefühl gezeichneten Trendgeraden zu flach oder zu steil erscheint - in jedem Fall also eine
Gerade, die der intuitiven (auf Normalabstände ausgerichteten) Vorstellung von einer gut
passenden Geraden nicht optimal entspricht (Abb. 19). Der Grund für diese Unzulänglichkeit
liegt im Verfahren - darauf soll hier jedoch nicht näher eingegangen werden.
Umsatz (in Mrd$)
180
2. Regressionsgerade
160
140
Trendgerade
120
100
80
1. Regressionsgerade
60
40
20
0
0
200.000
400.000
600.000
800.000
Beschäftigte
Abb. 19: Beschäftigtenzahlen und Umsätze in 35 Industrieunternehmen
Die beiden Regressionsgeraden lassen sich für jede Punktwolke ermitteln, also auch für
solche, bei denen kaum ein linearer Trend erkennbar ist. Ähnlich wie bei den Zentralmaßen
gilt auch hier: Bei entsprechend großer Streuung um die Trendgerade ist diese wenig
aussagekräftig und kaum geeignet, die vorliegenden Daten in geeigneter Weise zu
repräsentieren. Ein (auf Werte zwischen -1 und 1 genormtes) Maß für diese Streuung ist der
Pearsonsche Korrelationskoeffizient, dessen Formel sehr komplex und undurchsichtig
erscheint, der sich aber als Quadratwurzel aus dem Verhältnis der Steigungen der beiden
Regressionsgeraden (oder auch als geometrisches Mittel der Anstiege) doch recht anschaulich
erklären und anhand von Streudiagramm und Regressionsgeraden zumindest intuitiv auch
recht gut nachvollziehen lässt. Der Korrelationskoeffizient ist als ein Maß für die Repräsentativität der Regressionsgeraden zu verstehen; es kommt ihm damit in der zweidimensionalen
Statistik eine ähnliche Funktion zu, wie den Streuungsmaßen in der eindimensionalen
beschreibenden Statistik: Die Repräsentativität und Aussagekraft der Regressionsfunktion ist
umso geringer, je näher der Wert des Korrelationskoeffizienten bei null liegt (d. h., je stärker
die Daten um die Regressionsgeraden streuen bzw. je weiter die Regressionsgeraden
auseinanderklaffen).
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 16
Auch Trend bzw. Regression und Korrelation basieren wesentlich auf der Idee der (extremen)
Raffung: Ein großer, zweidimensionaler Datensatz wird durch eine einzige (meist lineare)
Funktion repräsentiert und ersetzt, die Streuung (Repräsentativität), wird durch einen einzigen
Koeffizienten beschrieben. Dabei gehen natürlich Informationen verloren, Strukturen und
Muster, die im Streudiagramm vielleicht noch erkennbar sind, verschwinden in der Regressions- und Korrelationsanalyse. So etwa könnte der nur mäßige Zusammenhang, die stark
streuenden Werte in Abb. 17 - 19 darauf zurückzuführen sein, dass die Zusammenhänge
zwischen Beschäftigtenzahlen und Umsätzen in unterschiedlichen Branchen sehr unterschiedlichen Trends folgen (vgl. die Clusterung nach Branchen in Abb. 20), die dann - wie die
Einkommen von Männern und Frauen in Abb. 16 - besser getrennt untersucht werden sollten.
Umsatz (in Mrd. $)
140
120
Fahrzeuge
100
Öl
Elektro
80
Metall
Tabak
60
Nahrungsmittel
Chemie
40
20
0
0
200.000
400.000
600.000
800.000
Beschäftigte
Abb. 20: Beschäftigtenzahlen und Umsätze in 35 Industrieunternehmen
Streudiagramm, Regressions- und Korrelationsanalyse verlangen metrische Daten. Bei der
Untersuchung von Zusammenhängen zwischen qualitativen Merkmalen wird man sich auf die
Darstellung in Tabellen und die Ermittlung eines Kontingenzkoeffizienten (der ähnlich wie der
Pearsonsche Korrelationskoeffizient zu interpretieren ist) beschränken müssen.
Bei der Interpretation von Trend, Regression, Korrelation bzw. Kontingenz ist Vorsicht
geboten: Zum einen sind Extrapolationen über den vorliegenden Datensatz hinaus jedenfalls
problematisch (z. B. längerfristige Prognosen bei Zeitreihen), weiters sollten Verallgemeinerungen, die über die vorliegenden Daten hinausgehen („Hochrechnungen“), der schließenden
Statistik vorbehalten bleiben und schließlich sind eventuell konstatierte Zusammenhänge zunächst nur formaler Art und ohne tiefere, kontextbezogene Einsichten in mögliche Ursachen
und Wirkung nicht kausal interpretierbar: Eine kausale Interpretation der hohen Korrelation
zwischen dem Verschwinden der Störche und dem drastischen Geburtenrückgang in einer
schwedischen Kleinstadt dürfte bei schulpflichtigen Kindern doch berechtigte Zweifel
auslösen; ob die häufigen Absenzen mancher Schüler die Ursache für schlechte Noten sind
oder die schlechten Noten Ursache für häufige Absenzen (oder ob der Zusammenhang doch
viel komplexer ist), lässt sich anhand von Regression und Korrelation allein nicht beurteilen.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 17
1. 5
Resumé
In der folgenden Tabelle sind die globalen Ideen, lokalen Bedeutungen und zentralen Tätigkeiten der beschreibenden Statistik noch einmal übersichtlich zusammengestellt:
BESCHREIBENDE STATISTIK
Ordnen und Darstellen von vorhandenen (erhobenen) Daten,
Charakterisierung der verfügbaren Daten und Aussagen darüber.
Globale Ideen
Lokale Bedeutungen
Zentrale Tätigkeiten
Möglichkeiten, Grenzen und Konkretisieren des Problems;
Probleme der Datenerhebung;
Erheben von Daten
Datentypen
MUSTER ERKENNEN
und
SICHTBAR MACHEN
RAFFUNG
Aussagekraft tabellarischer,
halbgrafischer oder grafischer
Darstellungen
Deutung diverser
Zentral- und Streuungsmaße,
von Trend (Regression) und
Korrelation bzw. Kontingenz
PFL-Mathematik 2000-02, Seminar 2,
Daten ordnen und
(tabellarisch oder grafisch)
übersichtlich darstellen
Kennzahlen ermitteln
„Stochastik in der Schule“ (Statement)
Seite 18
2
Wahrscheinlichkeitsrechnung im Dienste angewandter Statistik
Die Wahrscheinlichkeitsrechnung bildet heute meist den Schwerpunkt der (schulischen)
Stochastik. Bei aller Wertschätzung und Begeisterung für die mathematische Wahrscheinlichkeitstheorie halten wir dies für einen Fehler, der nicht zuletzt auf der (Fehl)Einschätzung
beruht, dass die beschreibende Statistik vielfach als zu einfach und elementar, die schließende
Statistik als zu schwierig für die Schule angesehen wird. Was dann bleibt ist die
Wahrscheinlichkeitstheorie, die in vielen Fällen auf Wahrscheinlichkeitsrechnung reduziert
wird, sich also vor allem um die Berechnung von Wahrscheinlichkeiten bemüht und weniger
um eine angemessene und verständige Interpretation der zentralen Begriffe und Sätze der
Wahrscheinlichkeitstheorie oder um die Rolle der Wahrscheinlichkeitstheorie als Bindeglied
zwischen den beiden Statistiken. Was Lernenden (wie auch Lehrenden) dabei den Zugang zu
zentralen Ideen der Wahrscheinlichkeitstheorie beträchtlich erschweren kann, ist die an vielen
einführenden Lehrbüchern nachvollziehbare Beobachtung,
-
-
-
-
-
dass grundlegende Begriffe (wie Ergebnis, Ereignis, Elementarereignis, Ergebnis- bzw.
Ereignisraum, Wahrscheinlichkeit, Zufallsvariable, Wahrscheinlichkeitsverteilung, Verteilungsfunktion, etc.) oft sehr formalistisch-exakt eingeführt werden, obwohl diese
Begriffe später gar nicht mehr, nicht in dieser Exaktheit oder überhaupt in ganz anderer
Form benötigt werden;
dass nicht selten unverständliche, gelegentlich auch falsche Erklärungen verwendet
werden;
dass die zahlreichen, zum Teil sehr diffizilen kombinatorischen Aufgaben die
Wahrscheinlichkeitsrechnung zur Kombinatorik umfunktionieren und vom eigentlichen
Anliegen der Wahrscheinlichkeitsrechnung ablenken;
dass der weitgehende Verzicht auf relevante statistische Fragestellungen die zahlreichen
Glücksspiele als zentrale “Anwendungen”, die Wahrscheinlichkeitsrechnung damit als
kaum ernst zu nehmende “Würfelbudenmathematik” erscheinen lässt;
dass die Wahrscheinlichkeitsrechnung oft wie ein Fremdkörper zwischen den beiden
Statistiken steht und nicht adäquat auf die schließende Statistik vorbereitet.
Im Folgenden wird ein Konzept der Wahrscheinlichkeitsrechnung skizziert und vorgeschlagen, das auf Kombinatorik und Glücksspiele weitgehend verzichtet, sich einer inhaltlichintuitiven Argumentation bedient und die Anliegen und Fragestellungen einer angewandten
Statistik in den Vordergrund stellt (vgl. Peschek 1995, 2000).
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 19
2. 1
Stichproben
Die beschreibende Statistik beschränkt sich im Wesentlichen auf Aussagen über vorliegende,
von ihr erhobene Daten. In der Praxis steht man aber nicht selten vor der Situation, dass man
an Aussagen über Daten interessiert ist, die man nicht oder nur mit unangemessen hohem
Aufwand vollständig erheben kann:
Wenn man wissen will, wie viele deutsche Familien ihren letzten Sommerurlaub im Ausland
verbracht haben, wird man kaum alle deutschen Familien befragen (eine derartige Befragung
wäre viel zu aufwendig), sondern man wird sich darauf beschränken, von einigen hundert
deutschen Familien zu erfahren, ob sie den letzten Sommerurlaub im Ausland verbrachten.
Die Funktionsfähigkeit von Streichhölzern testet man am besten durch Abbrennen. Es würde
aber wenig Sinn machen, alle 5 Milliarden Streichhölzer eines Lagers abzubrennen, um dann
festzustellen, dass der Ausschussanteil 2% betrug.
Bei vielen statistischen Untersuchungen wird man sich also auf Teilerhebungen, sogenannte
Stichproben, beschränken müssen, um dann von diesen Stichproben auf die interessierende
Grundgesamtheit zu schließen. Man nimmt dabei an, dass das Stichprobenergebnis in etwa
dem Wert in der Grundgesamtheit entsprechen wird und umgekehrt, also:
Parameter in der Grundgesamtheit  Parameter in der Stichprobe
Beispiel 3: Man stellt sich vor den Haupteingang der Universität Wien und befragt die einund ausgehenden Personen, ob sie Matura haben. 91 von 100 befragten Personen bejahen die
Frage - somit weiß man, dass ungefähr 91% aller Österreicher/innen Matura haben.
Es ist (uns) schon klar, dass es so nicht gehen kann. Offenbar ist aber das Problem der
geeigneten Stichprobenauswahl nicht allen (mit statistischen Zahlen operierenden) Menschen
als Problem bewusst (siehe Abb. 21).
Abb. 21: Kleine Zeitung, 13. 7. 1994, S. 39
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 20
Als Statistiker/in weiß man, dass man bei der Auswahl von Stichproben sehr behutsam sein
muss. Für die Stochastikausbildung erscheint es von Bedeutung, diese Problematik zu
thematisieren und einige Methoden der Stichprobenauswahl vorzustellen: Zufällige Auswahl
als theoretisches Konzept, das der Wahrscheinlichkeitsrechnung und der schließenden
Statistik zugrunde liegt, zufallsähnliche Verfahren (z. B. Buchstaben-, Geburtstags-,
Schlussziffernverfahren), Klumpenauswahl, geschichtete Stichproben als praktikablere
Methoden.
2. 2
Zwei Wahrscheinlichkeitsinterpretationen
Hat man eine “geeignete” Stichprobenauswahl getroffen, so stellt sich die Frage: „Was kann
man von dieser Stichprobe erwarten?” Überlegen wir anhand eines Beispiels:
Beispiel 4: Angenommen man weiß, dass 30% aller deutschen Familien ihren letzten
Sommerurlaub im Ausland verbracht haben. Was kann man erwarten, wenn man unter allen
deutschen Familien eine Familie zufällig auswählt (also die kleinstmögliche Stichprobe
zieht)?
Nun, man kann eine Familie mit Auslandsurlaub auswählen oder auch nicht, beides ist selbstverständlich möglich. Wenn man aber wetten müsste, würde man wohl kaum auf eine Familie
mit Auslandsurlaub setzen. Das hat mit deren eher niederen relativen Anteil in der
Grundgesamtheit (30%) zu tun. Es erscheint sinnvoll, diesen relativen Anteil als quantitatives
Maß für die Erwartung zu nehmen:
Wahrscheinlichkeit als relativer Anteil in der Grundgesamtheit
Wird unter allen Elementen einer endlichen Grundgesamtheit G ein Element zufällig
ausgewählt, so kann man als Maß für die Erwartung, genau ein Element einer Teilmenge A
auszuwählen, den relativen Anteil h(A) (mit h(A)=a/g; a bzw. g meint die Mächtigkeit von A
bzw. G) nehmen. Man schreibt:
P(E) = h(A)
wobei P(E) die Wahrscheinlichkeit für das Ereignis E angibt, dass ein aus G zufällig
ausgewähltes Element der Teilmenge A angehört.
Man sieht: Die Wahrscheinlichkeitsrechnung quantifiziert das Maß der Erwartung durch eine
dem relativen Anteil entsprechende Zahl zwischen 0 und 1.
Für die Untersuchung größerer Stichproben, die man als längere Serien derartiger Zufallsversuche auffassen kann, hilft diese Wahrscheinlichkeitsinterpretation nur beschränkt weiter.
Hilfreich ist in diesem Fall aber die als Empirisches Gesetz der großen Zahlen bekannte
Erfahrungstatsache, dass sich die relative Häufigkeit h(E) eines Ereignisses (h(E) = k/n, wenn
das Ereignis E unter den ersten n Versuchen k mal eingetreten ist) mit zunehmender
Versuchsanzahl um einen festen Wert “stabilisiert” (Abb. 22).
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 21
Abb. 22: „Stabilisierung“ der relativen Häufigkeiten
Diese empirische Erfahrungstatsache legt eine weitere Wahrscheinlichkeitsinterpretation
nahe:
Wahrscheinlichkeit als relative Häufigkeit in einer Versuchsserie
Nach dem Empirischen Gesetz der großen Zahlen “stabilisieren” sich die relativen Häufigkeiten h(E) in einer Versuchsserie um einen festen Wert, und es erscheint zweckmäßig, diesen
Wert als Wahrscheinlichkeit für das Ereignis E zu nehmen:
h(E)  P(E)
2. 3 Zusammenhang zwischen Grundgesamtheit und Stichprobe
Mit Hilfe dieser beiden Wahrscheinlichkeitsinterpretationen lässt sich der Zusammenhang
zwischen Parameter der Stichprobe und der Grundgesamtheit genauer erklären:
Die relative Häufigkeit eines Ereignisses E in einer (längeren) Versuchsserie (Stichprobe) ist
ungefähr gleich der Wahrscheinlichkeit für dieses Ereignis E: h(E)  P(E)
Die Wahrscheinlichkeit für ein Ereignis E ist aber gleich dem relativen Anteil dieses
Ereignisses E in der Grundgesamtheit: P(E) = h(A)
Beide Wahrscheinlichkeitsinterpretationen zusammen erklären den (bisher spekulativen oder
empirischen) Zusammenhang zwischen Stichprobe (Stpr) und Grundgesamtheit (Gg) mit
Hilfe des Wahrscheinlichkeitsbegriffs:
h(E)  P(E) = h(A)
Stpr
<  >
Gg
Diese Gleichungskette von links nach rechts gelesen, zeigt eine globale Idee der schließenden
Statistik, nämlich den Schluss von der Stichprobe auf die Grundgesamtheit
(“Hochrechnung”).
Die Gleichungskette von rechts nach links gelesen, verweist auf den Schluss von der
Grundgesamtheit auf die Stichprobe und damit auf die im Hinblick auf eine angewandte
Statistik zentrale Frage der Wahrscheinlichkeitsrechnung, nämlich:
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 22
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 23
2. 4
Was kann man von einer “pflichtbewussten” Stichprobe erwarten?
Beispiel 5: Angenommen man weiß, dass 30% aller deutschen Familien ihren letzten
Sommerurlaub im Ausland verbracht haben. Was kann man erwarten, wenn man 50 deutsche
Familien zufällig auswählt und sie entsprechend befragt?
-
-
-
Es ist sehr unwahrscheinlich, dass man nur Familien erhält, die ihren Sommerurlaub im
Ausland verbracht haben: P(B=50) = 0,3  0,3  0,3  ...  0,3 = 0,350  0
(Bei der Ermittlung dieser Wahrscheinlichkeit kommt die Multiplikationsregel für
unabhängige Ereignisse zur Anwendung.)
Es ist fast ebenso unwahrscheinlich, dass keine der befragten 50 Familien ihren
Sommerurlaub im Ausland verbracht hat: P(B=0) = 0,7  0,7  0,7  ...  0,7 = 0,750  0
Die Wahrscheinlichkeit, dass 49 der befragten Familien im letzten Sommer im Ausland
waren, ist auch nicht sehr viel größer: P(B=49) = 50  0,349  0,7  0
(Zur Multiplikationsregel für unabhängige Ereignisse kommt hier die Additionsregel für
einander ausschließende Ereignisse hinzu.)
Analoges gilt für die Wahrscheinlichkeit, dass nur eine Familie im Ausland war:
P(B=1) = 50  0,3  0,749  0
Die Wahrscheinlichkeiten P(B=2), P(B=3), ..., P(B=48) sind umständlicher zu berechnen – es
empfiehlt sich, sich über den Typ der Wahrscheinlichkeitsverteilung Klarheit zu verschaffen,
um sich dann entsprechender Formeln, Tabellen oder Computersoftware zu bedienen. In
unserem Beispiel erhält man für (die Zufallsgröße) B = 0, 1, ... , 50 eine Binomialverteilung
bzw. eine durch Binomialverteilung approximierbare Hypergeometrische Verteilung (je nachdem, ob man immer aus allen deutschen Familien auswählt oder nur aus jenen, die zuvor noch
nicht ausgewählt wurden) mit Erwartungswert (“Mittelwert”) µ und Standardabweichung
(“Streuung”) . In vielen praktisch relevanten Fällen (nicht zu kleine Stichprobe aus einer
sehr viel größeren Grundgesamtheit) sind die beiden Verteilungen einander sehr ähnlich und
durch eine Normalverteilung gut approximierbar.
P(B = k)
0,14
0,12
0,1
0,08
0,06
0,04
0,02
k
0
1 3 5 7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
Abb. 23: Binomialverteilung mit n=50, p=0,3
Aus der in Abb. 23 grafisch dargestellten Wahrscheinlichkeitsverteilung erkennt man, dass
np=15 Familien mit Auslandsurlaub am wahrscheinlichsten sind. Aber auch 13, 14, 16, 17
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 24
Familien wären keine besondere Überraschung. Müsste man wetten, so wäre es ziemlich
riskant, auf genau 15 Familien zu setzen, also eine “Punktschätzung” abzugeben (die Wahrscheinlichkeit dafür ist nur ca. 12%). Man geht jedoch kein allzu großes Risiko ein, wenn man
z. B. prognostiziert, dass es “zwischen 10 und 20 Familien” sein werden, die ihren letzten
Sommerurlaub im Ausland verbracht haben, wenn man also eine “Intervallschätzung” macht
(die Wahrscheinlichkeit dafür ist in diesem Beispiel ca. 92%).
Damit haben wir eine Antwort auf die für die (angewandte) Statistik wesentlichste Frage an
die Wahrscheinlichkeitsrechnung gefunden: Mit hoher Wahrscheinlichkeit  (hier 92%) wird
man eine Stichprobe ziehen, in der es 10, 11, ...., 19 oder 20, also zwischen 10 und 20
Familien gibt, die ihren letzten Sommerurlaub im Ausland verbracht haben. Ein derartiges
Intervall, in dem der untersuchte Parameter der Stichprobe - in unserem Fall die (relativen)
Häufigkeiten - mit einer gewissen Wahrscheinlichkeit  liegt, nennt man einen Schätzbereich (für relative Häufigkeiten). Der  - Schätzbereich ist somit die mathematische
Antwort auf die zentrale Frage der Wahrscheinlichkeitsrechnung.
Zu einem solchen  - Schätzbereich lassen sich drei verschiedene, praktisch durchaus
relevante Typen von Fragestellungen formulieren:
Beispiel 6 (gegeben n und , gesucht ): Wie viele deutsche Familien mit Auslandsurlaub kann
man in einer Stichprobe von 1000 zufällig ausgewählten Familien mit 95% Sicherheit
erwarten?
Beispiel 7 (gegeben n und , gesucht ): Mit welcher Wahrscheinlichkeit findet man unter
1000 zufällig ausgewählten deutschen Familien zwischen 145 und 155 Familien mit
Auslandsurlaub?
Beispiel 8 (gegeben  und , gesucht n): Wie viele deutsche Familien muss man zufällig
auswählen, damit man mit 95% Sicherheit mindestens 145 (höchstens 155; zwischen 145 und
155) Familien mit Auslandsurlaub in der Stichprobe hat?
2. 5
Resumé:  - Schätzbereich als globale Idee
Wir sind davon ausgegangen, dass man den relativen Anteil p in der Grundgesamtheit kennt
und haben dann die etwas unpräzise Vermutung aufgestellt, dass man von einer geeigneten
Stichprobe erwarten kann, dass der entsprechende Stichprobenanteil ebenfalls ungefähr p
beträgt. Mit Hilfe der Wahrscheinlichkeitsrechnung lässt sich diese Aussage nun
mathematisch präzisieren und quantifizieren:
“erwarten”:
“ungefähr”:
Wahrscheinlichkeit 0  P  1 als quantitatives Maß für diese Erwartung
Angabe eines (i. A. um p symmetrischen) Intervalls
Zusammengefasst heißt dies: Mit (hoher) Wahrscheinlichkeit  liegt der Stichprobenanteil im
Intervall [p - ; p + ].
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 25
Dieses Intervall [p - ; p + ] ist, zusammen mit der Wahrscheinlichkeit , eine sinnvolle Antwort auf die Frage, was man von einer geeigneten Stichprobe erwarten kann; man nennt dieses
Intervall  - Schätzbereich für die relativen Häufigkeiten in der Stichprobe (siehe Abb. 24).
P(B = k)
k
-Schätzbereich
Abb. 24:  - Schätzbereich einer Wahrscheinlichkeitsverteilung
Will man einen Schätzbereich mit hoher Wahrscheinlichkeit (Sicherheit) , so bedeutet dies,
dass der Schätzbereich breiter, die Aussage somit “ungenauer” wird. Will man umgekehrt die
“Präzision” der Aussage erhöhen, also den Schätzbereich verkleinern, so wird dadurch die
Wahrscheinlichkeit (Sicherheit) , mit der die getroffene Aussage zutrifft, sinken. Es wird also
in jedem Fall nötig sein, einen im Hinblick auf den Kontext adäquaten Mittelweg zwischen
“Präzision” und Sicherheit der Aussage zu finden.
Mit diesem  - Schätzbereich hat man die für die angewandte Statistik globale Idee der
Wahrscheinlichkeitsrechnung herausgearbeitet. Je nach Problemstellung bzw. Modellierung
wird man diese Idee auf Binomialverteilungen, Hypergeometrische Verteilungen, StudentVerteilungen, Chi2-Verteilungen oder andere Wahrscheinlichkeitsverteilungen, insbesondere
auch auf die Normalverteilung, anzuwenden haben. Die Grundidee bleibt dabei von der Art
der Verteilung unberührt.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 26
In der folgenden Tabelle sind die im Hinblick auf eine angewandte Statistik globale Idee der
Wahrscheinlichkeitsrechnung, die lokalen Bedeutungen und die damit erforderlichen
zentralen Tätigkeiten in übersichtlicher Form zusammengefasst:
WAHRSCHEINLICHKEITSRECHNUNG
Aus bekannten Wahrscheinlichkeiten werden neue (noch unbekannte)
Wahrscheinlichkeiten berechnet.
Globale Idee
Lokale Bedeutungen
Zentrale Tätigkeiten
Stichprobe als Serie von
Zufallsversuchen
Ziehen von Stichproben
Zwei Wahrscheinlichkeitsinterpretationen
 - SCHÄTZBEREICH
als mathematische Antwort
auf die zentrale Frage der
Wahrscheinlichkeitsrechnung:
Was kann man von
“pflichtbewussten”
Stichproben erwarten?
(Mathematisierung von
Stpr  Gg)
PFL-Mathematik 2000-02, Seminar 2,
Deutung von Addition und
Multiplikation
Anwendungsbereiche und
Eigenschaften diverser
Wahrscheinlichkeitsverteilungen
 - Schätzbereich als
Intervall, in dem
Stichprobenergebnisse mit
Wahrscheinlichkeit  liegen
Addieren und Multiplizieren
von Wahrscheinlichkeiten
Arbeiten mit verschiedenen
Wahrscheinlichkeitsverteilungen;
Lage- und Streuungsparameter;
Approximieren mit
Normalverteilung
Ermitteln von  Schätzbereichen
„Stochastik in der Schule“ (Statement)
Seite 27
3.
Zwei grundlegende Ideen der schließenden Statistik
Jede/r von uns kennt das: Nach dem dritten BMW-Fahrer, der uns mit Blinkzeichen und
Lichthupe nötigt die Überholspur augenblicklich zu verlassen, sind wir davon überzeugt, dass
BMW-Fahrer – oder zumindest die meisten unter ihnen – rücksichtslose Raser sind. Entsprechendes gilt für Politiker/innen nach dem zweiten Bestechungsskandal und für die
mathematische (Un-)Begabung von Mädchen, nachdem wir in kurzer Zeit bei fünf Mädchen
Lernschwierigkeiten in Mathematik beobachtet haben. Wir verallgemeinern (weil es uns
solche Verallgemeinerungen und Kategorisierungen leichter machen, die Komplexität unserer
Umwelt zu bewältigen), wir schließen von einigen Einzelbeobachtungen auf die Gesamtheit.
Werden wir mit derartigen verallgemeinernden Behauptungen konfrontiert ohne selbst bislang
bewusst derartige Beobachtungen gemacht zu haben, werden wir – falls uns der Sachverhalt
interessiert – versuchen, diese Behauptung durch eigene Beobachtungen zu „verifizieren“ oder
zu widerlegen.
Die schließende Statistik bietet mit der „Hochrechnung“ (Vertrauensintervall) und dem
Hypothesentest zwei globale Ideen an, wie dem zuvor kurz skizzierten Alltagsverhalten ein
standardisiertes, normiertes, quantitatives Verfahren zur Seite (oder auch gegenüber) gestellt
werden könnte. Dabei spielen die zuvor beschriebenen  - Schätzbereiche eine zentrale Rolle:
3. 1
Testen von Hypothesen
Die Grundidee des Testens von Hypothesen ist relativ einfach: Man geht von einer
Vermutung, Annahme, Behauptung, allgemein von einer Hypothese (etwa über den relativen
Anteil p eines Merkmals in der Grundgesamtheit) aus. Zur Überprüfung dieser Hypothese
wird eine (Zufalls-) Stichprobe gezogen.
Wenn die Hypothese richtig ist, kann man mit (großer) Wahrscheinlichkeit  damit rechnen,
dass die relative Häufigkeit des Merkmals in der Stichprobe im  - Schätzbereich liegt. Liegt
die relative Häufigkeit der Stichprobe dann tatsächlich innerhalb des  - Schätzbereichs, so ist
das Stichprobenergebnis mit der Hypothese kompatibel, und man wird die Hypothese nicht
zurückweisen können. (Bewiesen ist sie damit allerdings nicht!).
Für den Fall hingegen, dass das Stichprobenergebnis außerhalb des  - Schätzbereichs liegt,
kann man sich Folgendes überlegen: Nimmt man an, dass die Hypothese stimmt (und sowohl
Stichprobenauswahl als auch Befragung korrekt durchgeführt wurden), so ist ein Stichprobenergebnis aufgetreten, das sehr unwahrscheinlich ist (einen solchen Stichprobenwert
wird man nur sehr selten, nämlich in  = 1 -  aller Fälle, beobachten). Ehe man an einem
derart unwahrscheinlichen Ergebnis festhält, wird man wohl eher annehmen, dass die
Hypothese unzutreffend ist und sie daher zurückweisen (ablehnen).
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 28
Beispiel 9: Der Leiter eines Fremdenverkehrsbüros behauptet, dass 40% aller deutschen
Familien ihren letzten Sommerurlaub im Ausland verbracht haben.
Wenn diese Behauptung richtig ist, dann wird man in einer Stichprobe von n = 200 mit einer
Wahrscheinlichkeit von 95% (also in durchschnittlich 95 von 100 Stichproben) zwischen 66
(33%) und 94 (47%) Familien finden, die ihren letzten Sommerurlaub im Ausland verbracht
haben. Das heißt, ein Stichprobenergebnis zwischen 33% und 47% wird mit der Behauptung
verträglich sein und man wird in einem solchen Fall die Behauptung nicht zurückweisen
können.
Falls die Behauptung stimmt, ist jedoch ein Stichprobenergebnis, das außerhalb des Bereichs
[0,33; 0,47] liegt, sehr unwahrscheinlich: man kann mit einem derartigen Stichprobenergebnis
durchschnittlich nur in 5 von 100 Fällen rechnen. Tritt ein solcher Fall ein, so sind Zweifel an
der Richtigkeit der Behauptung durchaus angebracht; man wird die Behauptung (mit einer
Irrtumswahrscheinlichkeit von  = 5%) zurückweisen und behaupten, dass unter allen
deutschen Familien der Anteil der Familien, die ihren letzten Sommerurlaub im Ausland
verbracht haben, ungleich 40% ist (vgl. Abb. 25).
Bei dieser Formulierung wurde nach zwei Seiten (relative Anteil größer oder auch kleiner
40%) getestet. Häufiger wird die Behauptung so formuliert sein, dass nur nach einer Seite
getestet werden muss (etwa bei der Behauptung, dass der relative Anteil mehr als 40%
beträgt). In Abb. 25 ist auch ersichtlich, wie Testergebnisse bei einseitiger Hypothese
interpretiert werden können: Bei Testergebnissen über 47% ist die Behauptung p > 40% (mit
einer Irrtumswahrscheinlichkeit von 2,5%) „statistisch bewiesen“, bei Testergebnissen unter
33% ist sie „statistisch widerlegt“.
40 %
G ru n d g e s a m th e it
 /2 = 2 ,5 %
p
a /2 = 2 ,5 %
 = 95 %
S tic h p ro b e
h
33 %
m it H : p = 4 0 % u n v e rträ g l.
S tic h p ro b e n e rg e b n is s e
p < 4 0 % " s ta t. b e w ie s e n "
40 %
4 0 % -S c h ä tz b e re ic h
m it H : p = 4 0 % v e rträ g lic h e
S tic h p rio b e n e rg e b n is s e
47%
m it H : p = 4 0 % u n v e rträ g l.
S tic h p ro b e n e rg e b n is s e
p > 4 0 % " s ta t. b e w ie s e n "
Abb. 25: Testen von Hypothesen anhand eines 95%-Schätzbereichs
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 29
3. 2
Vertrauensintervalle
Die “Hochrechnung” geht nicht von Annahmen, Vermutungen, Behauptungen über Parameter
der Grundgesamtheit aus, sondern versucht Parameter der Grundgesamtheit mittels
Stichproben zu “schätzen”: Man kennt, beobachtet, ermittelt etwa die relative Häufigkeit h‘
eines Ereignisses in einer Stichprobe und “schätzt” mit diesem Wert (mit einer gewissen
Unsicherheit und Unschärfe) den entsprechenden Wert in der Grundgesamtheit. Dabei geht
man von der Überlegung aus, dass - sofern es sich nicht um ein extremes Stichprobenergebnis
handelt - das Stichprobenergebnis h‘ im  - Schätzbereich um den gesuchten relativen Anteil p
in der Grundgesamtheit liegt. Das  - Konfidenzintervall (Vertrauensintervall) für den
relativen Anteil p in der Grundgesamtheit kann somit als die Menge aller p, deren  Schätzbereiche die in der Stichprobe beobachtete relative Häufigkeit h‘ enthalten, betrachtet
(definiert) werden (Abb. 26).
pu
- Konfidenzintervall
po
Grundgesamtheit
Stichprobe
pu + 
u = h’ = po - 
o
- Schätzbereich
- Schätzbereich
Abb. 26:  - Konfidenzintervall
Das in Abb. 26 dargestellte Konfidenzintervall lässt sich nicht ganz einfach ermitteln - bei
praktischen Berechnungen wird man es meist durch ein um h‘ symmetrisches Intervall
approximieren. Bei Annahme einer Normalverteilung etwa erhält man als Konfidenzintervall für den relativen Anteil p in der Grundgesamtheit näherungsweise

h '  (1  h ' ) '
h '  (1  h ' ) 
 h'  z 
 mit 2 ( z)  1  
;h  z
n
n


PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 30
3. 3
Resumé
In der folgenden Tabelle sind die zwei globalen Ideen, lokale Bedeutungen und zentrale Tätigkeiten der schließenden Statistik in einer Übersicht zusammengestellt:
SCHLIESSENDE STATISTIK
Vermutungen bzw. Behauptungen (Hypothesen) über Parameter der Grundgesamtheit
(z. B. relativer Anteil bzw. Wahrscheinlichkeit) anhand von Stichproben überprüfen;
Schätzwerte (Intervalle) für Parameter anhand von Stichproben ermitteln.
Globale Ideen
TESTEN VON
HYPOTHESEN
HOCHRECHNUNG
Lokale Bedeutungen
Was bedeutets es, wenn ein
Stichprobenergebnis nicht im
Schätzbereich liegt?
Ablehnen und Beweisen von
Hypothesen;
Fehler erster und zweiter Art:
Einfluss der Stichprobengröße
und der Abweichung des
Hypothesenwerts vom
tatsächlichen Wert
Zentrale Tätigkeiten
Schätzbereiche ermitteln
Interpretation des
Konfidenzintervalls;
Stichprobenumfang,
Konfidenzintervalle berechnen;
Intervallbreite und Sicherheit;
Stichprobenumfang festlegen
Zusammenhang mit Schätzbereich und Hypothesentest
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 31
4.
Konkretisierungen des vorgestellten Konzepts und Literaturhinweise
Bei dem hier skizzierten Konzept handelt es sich um ein Konzept traditioneller, klassischer
Stochastik, in dem etwa die Explorative Datenanalyse kaum, die Bayesianische Statistik oder
die Rolle von Statistiksoftware nicht explizit angesprochen werden (entsprechende
Erweiterungen sind in diesem Konzept aber durchaus möglich).
Dieses Konzept wird von den Autoren/innen seit mehreren Jahren in der statistischen
Grundausbildung von Betriebswirt/inn/en wie auch in der didaktischen Aus- und
Weiterbildung von Lehrer/inne/n eingesetzt und es war Basis für die Entwicklung von
Lehrbüchern für „Handelsakademien“ (eine Art Gymnasium oder Fachoberschule
wirtschaftlicher Ausrichtung) und für die Ausbildung von Wirtschaftswissenschaftler/inne/n
(Kronfellner/Peschek 1998 bzw. Kröpfl u. a. 1999) an Universitäten und Fachhochschulen.
Weitere Beispiele, Konkretisierungen und Vertiefungen verschiedener hier angeführter Überlegungen findet man in vielen (didaktischen) Arbeiten zur Stochastik – hier sei lediglich
beispielhaft auf (Kütting 1994a), (Kütting 1994b), (Reichel/Hanisch/Müller 1987) und
(Tietze/Klika/ Wolpers 1982) hingewiesen.
Literatur
Fischer, R. (1986): Zum Verhältnis von Mathematik und Kommunikation. In: mathematica
didactica 9, S. 119-131.
Fischer, R. und Malle, G. (1989): Mensch und Mathematik. Eine Einführung in didaktisches
Denken und Handeln. B. I. Wissenschaftsverlag, Mannheim-Wien-Zürich.
Kronfellner, M. und Peschek, W. (1998): Angewandte Mathematik 4. öbv&hpt, Wien.
Kröpfl, B. u. a. (1999): Angewandte Statistik. Eine Einführung für Wirtschaftswissenschaftler.
2. Auflage. Hanser, München-Wien.
Kütting, H. (1994a): Beschreibende Statistik im Schulunterricht. B. I. Wissenschaftsverlag,
Mannheim-Leipzig-Wien-Zürich.
Kütting, H. (1994b): Didaktik der Stochastik. B. I. Wissenschaftsverlag, Mannheim-LeipzigWien-Zürich.
Peschek, W. (1995): Wahrscheinlichkeitsrechnung im Rahmen einer Angewandten Statistik.
In: Müller, K. P. (Hrsg.): Beiträge zum Mathematikunterricht 1995. Franzbecker,
Hildesheim, S. 372 – 75.
Peschek, W. (1998): Beschreibende Statistik: Zentrale Tätigkeiten, lokale Bedeutungen,
globale Ideen. In: Didaktikheft, Schriftenreihe der Österreichischen Mathematischen
Gesellschaft zur Didaktik der Mathematik an Höheren Schulen, Heft 29. ÖMG, Wien
1998, S. 134-149.
Peschek, W. (2000): Was kann man von `pflichtbewusstenA Stichproben erwarten? Wahrscheinlichkeitsrechnung im Dienste angewandter Statistik. Erscheint in:
Didaktikheft, Schriftenreihe der Österreichischen Mathematischen Gesellschaft zur
Didaktik der Mathematik an Höheren Schulen, ÖMG, Wien.
Reichel, H.-C., Hanisch, G. und Müller, R. (1987): Wahrscheinlichkeitsrechnung und
Statistik. Verlag Hölder-Pichler-Tempsky, Wien.
Tietze, U.-P., Klika, M. und Wolpers, H. (1982): Didaktik des Mathematikunterrichts in der
Sekundarstufe II. Vieweg, Braunschweig.
PFL-Mathematik 2000-02, Seminar 2,
„Stochastik in der Schule“ (Statement)
Seite 32