Aufgabe 13 Man betrachtet als Zufallsexperiment den einfachen

Statistik II für Studierende der Soziologie und Nebenfachstudierende
Dr. Carolin Strobl, Gero Walter
Übungsblatt 4
SoSe 2009
Aufgabe 13
Man betrachtet als Zufallsexperiment den einfachen Würfelwurf mit einem fairen Würfel, d.h. die Augenzahlen 1 bis 6 sind jeweils gleichwahrscheinlich. Das
Experiment werde durch die Zufallsvariable X beschrieben.
a) Wie lautet der Träger der Verteilung von X?
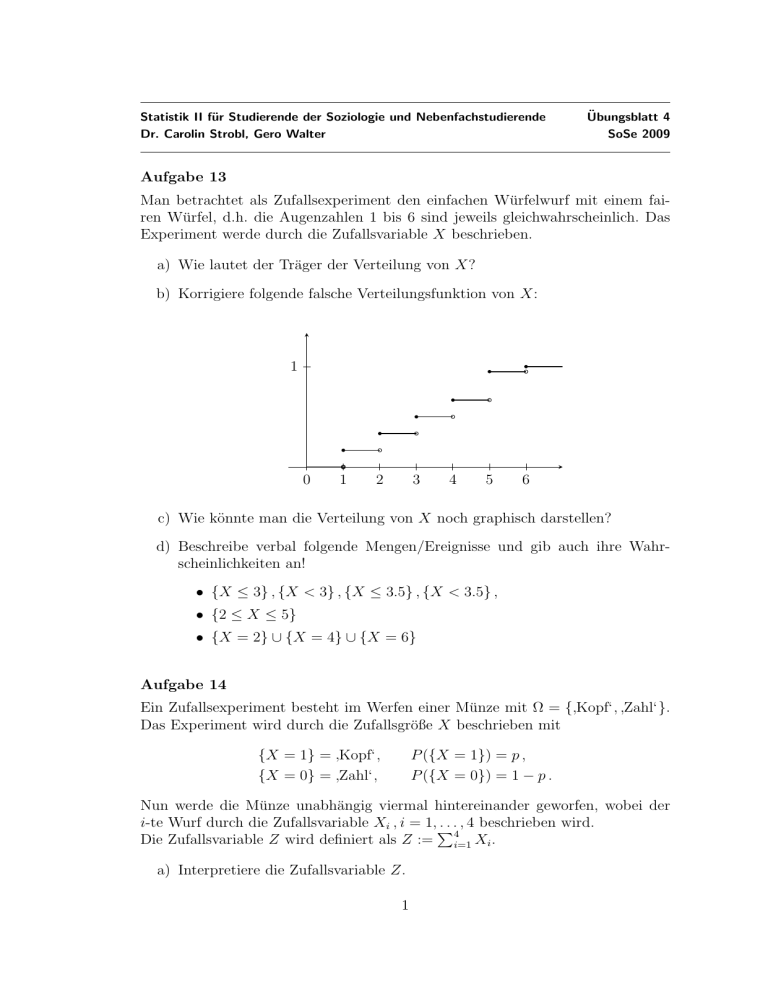
b) Korrigiere folgende falsche Verteilungsfunktion von X:
1
0
1
2
3
4
5
6
c) Wie könnte man die Verteilung von X noch graphisch darstellen?
d) Beschreibe verbal folgende Mengen/Ereignisse und gib auch ihre Wahrscheinlichkeiten an!
• {X ≤ 3} , {X < 3} , {X ≤ 3.5} , {X < 3.5} ,
• {2 ≤ X ≤ 5}
• {X = 2} ∪ {X = 4} ∪ {X = 6}
Aufgabe 14
Ein Zufallsexperiment besteht im Werfen einer Münze mit Ω = { Kopf‘, Zahl‘}.
’
’
Das Experiment wird durch die Zufallsgröße X beschrieben mit
{X = 1} = Kopf‘,
’
{X = 0} = Zahl‘,
’
P ({X = 1}) = p ,
P ({X = 0}) = 1 − p .
Nun werde die Münze unabhängig viermal hintereinander geworfen, wobei der
i-te Wurf durch die Zufallsvariable Xi , i = 1, P
. . . , 4 beschrieben wird.
Die Zufallsvariable Z wird definiert als Z := 4i=1 Xi .
a) Interpretiere die Zufallsvariable Z.
1
b) Welche Werte kann Z mit positiver Wahrscheinlichkeit annehmen?
c) Berechne die Wahrscheinlichkeiten P ({Z = 0}), P ({Z = 1}), P ({Z = 4}).
Aufgabe 15
Betrachte folgende Rechenregeln‘ für den Erwartungswert und die Varianz mit
’
den Zufallsvariablen X und Y . Gib jeweils an, ob die Regeln richtig sind, bzw.
unter welchen Bedingungen sie korrekt sind!
?
a) E(X + a) = E(X)
?
b) E(Y + X) = E(X) + E(Y )
?
c) E(X − Y ) = 0
?
d) Var(X + Y ) = Var(X) + Var(Y )
?
e) Var(X − Y ) = Var(X) − Var(Y )
?
f) E(X 2 ) = Var(X)
?
g) Var(aX) = aVar(X)
Aufgabe 16
Eine Zufallsvariable X nimmt die Werte 1 und −1 jeweils mit Wahrscheinlichkeit
0.5 an. Nun wird die Zufallsvariable Y definiert mit Y := 3 + 2 · X.
a) Wie sieht die Verteilung von Y aus?
b) Bestimme Erwartungswert und Varianz von X und Y .
Aufgabe 17
Eine Zufallsvariable X sei standardnormalverteilt.
a) Skizziere die Dichte sowie die Verteilungsfunktion.
b) Bestimme die Wahrscheinlichkeit für die Menge {X < 1.96} aus der Tabelle.
c) Wie findet man graphisch anhand der Dichte bzw. anhand der Verteilungsfunktion die gesuchte Wahrscheinlichkeit?
2
Aufgabe 18
a) Interpretiere folgende Formeln zur Analyse von Lebensdauern:
P (t ≤ T ≤ t + h | T ≥ t)
P (t ≤ T ≤ t + h | T ≥ t)
λ(t) := lim
h→0
h
b) Eine Zufallsvariable T mit Parameter λ > 0 und Dichte f (t) = λ exp(−λt)
heißt exponentialverteilt für t ≥ 0, Kurzform T ∼ Exp(λ).
• Zeige, dass es sich bei f (t) um eine Dichte handelt.
• Berechne und interpretiere die Hazardrate.
c) Eine Zufallsvariable T heißt weibullverteilt mit Parametern λ > 0, α > 0,
falls ihre Dichte für t ≥ 0 folgende Gestalt hat:
f (t) = λα(λt)α−1 exp(−(λt)α )
Die Survivorfunktion von T lautet S(t) = exp(−(λt)α ) , t ≥ 0.
• Bestimme daraus die Hazardrate von T .
Welcher Spezialfall ergibt sich für α = 1?
• Betrachte die Hazardraten für α < 1, α = 1 und α > 1 (siehe Graphik
auf der nächsten Seite). Zur Modellierung welcher Situationen sind die
verschiedenen Verläufe der Hazardrate λ(t) geeignet? Erfinde je ein
Beispiel.
d) Angenommen, wir haben Daten über die Dauer von Arbeitslosigkeit bis
zum Berufs-Wiedereinstieg.
• Was bedeueten die in a) aufgeführten Größen in diesem Beispiel?
• Lässt sich dieses Beispiel auch mit einem Markovmodell modellieren?
Was wären hier die relevanten Größen?
3
Hazardraten einer Weibullverteilung (λ = 0.5)
1.6
1.4
α=3
α = 1/3
1.2
1
0.8
0.6
α=1
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
x
4
1.2
1.4
1.6
1.8
2