Vorwort

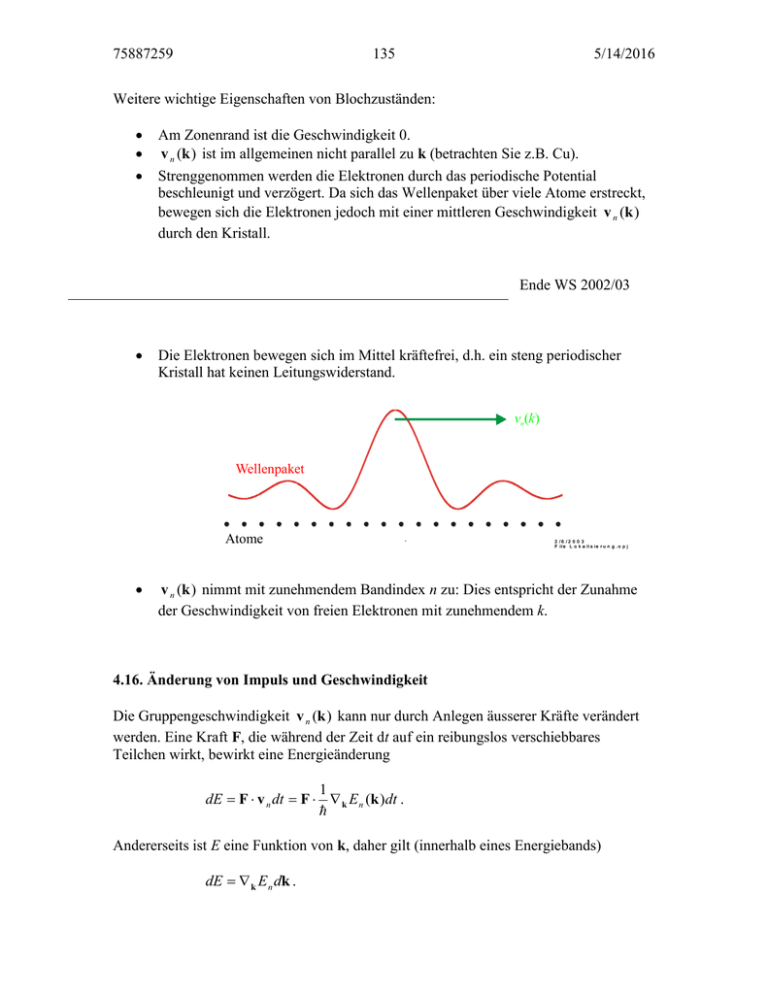
75887259
135
5/14/2016
Weitere wichtige Eigenschaften von Blochzuständen:



Am Zonenrand ist die Geschwindigkeit 0.
v n (k ) ist im allgemeinen nicht parallel zu k (betrachten Sie z.B. Cu).
Strenggenommen werden die Elektronen durch das periodische Potential
beschleunigt und verzögert. Da sich das Wellenpaket über viele Atome erstreckt,
bewegen sich die Elektronen jedoch mit einer mittleren Geschwindigkeit v n (k )
durch den Kristall.
Ende WS 2002/03

Die Elektronen bewegen sich im Mittel kräftefrei, d.h. ein steng periodischer
Kristall hat keinen Leitungswiderstand.
vn(k)
Wellenpaket
Atome

.
2 /6 /2 0 0 3
F ile L o k a lis ie r u n g . o p j
v n (k ) nimmt mit zunehmendem Bandindex n zu: Dies entspricht der Zunahme
der Geschwindigkeit von freien Elektronen mit zunehmendem k.
4.16. Änderung von Impuls und Geschwindigkeit
Die Gruppengeschwindigkeit v n (k ) kann nur durch Anlegen äusserer Kräfte verändert
werden. Eine Kraft F, die während der Zeit dt auf ein reibungslos verschiebbares
Teilchen wirkt, bewirkt eine Energieänderung
1
dE  F  v n dt  F   k E n (k )dt .

Andererseits ist E eine Funktion von k, daher gilt (innerhalb eines Energiebands)
dE   k E n dk .
75887259
136
Gleichsetzen liefert:
5/14/2016
F
dt  dk .

Damit erhält man die halb-klassische Bewegungsgleichung:
F
dk
 k .
dt
Die Kristallimpulsänderung pro Sekunde ist gleich der angelegten,
phänomenologischen Kraft.
Beispiel Lorentz-Kraft (SI Einheiten):
k  eE(r , t )   v n (k)  B(r, t )
Grenzen der Anwendbarkeit:




Wellenpaket muss sich viel weiter ausdehnen als die Gitterkonstante
Wellenpaket viel breiter als Wellenlänge der räumlichen Variation des angelegten
Feldes
Für B sollte man im Sinne der räumlichen Mittelung  0 H einsetzen.
Felder sollen schwach sein (siehe Ashcroft Mermin), beachte kleine Bandgaps
Aufgrund des 2. Newton’schen Gesetzes, wird eine Masse durch Anlegen einer Kraft
beschleunigt
F  ma .
Die hier eingesetzte Masse m bedeutet in diesem Ausdruck eine sogenannte “effektive”
Masse, die aufgrund der Wechselwirkung der Elektronen von der Ruhemasse des
Elektrons abweichen wird. Es ist naheliegend, eine effektive Masse m * mit Hilfe der
Definition der Beschleunigung einzuführen.
Für die Beschleunigungskomponente a i ( i  x, y, z ) erhält man
ai 
dvi 1 d En (k ) 1  dEn (k ) 1 
dk



 k En (k )

dt  dt k i
 k i dt
 k i
dt
ai 
 2 En 
 2 En 
1  2 En 
(
kx 
ky 
kz ) .
 k i k x
k i k y
k i k z
Aufgrund von F  k folgt
ai 
Fy
F
F
1  2 En
1  2 En
1  2 En
F

F

Fz  x 
 z .
x
y
2
2
2
mix miy miz
 k i k x
 k i k y
 k i k z
75887259
137
5/14/2016
Die Koeffizienten der Kraftkomponenten haben die Dimension einer Masse, die durch
einen symmetrischen Tensor 2. Stufe gegeben ist, dessen Elemente definiert sind durch
 1 
1 2E
 *   2
.
 mn  ij  k i k j
Die halbklassische Bewegungsgleichung lautet damit:
 1 
v   *  F .
 m n  ij
Bemerkungen:

Es ist klar, dass insbesondere in der Nähe von kritischen Punkten der Fermifläche
die effektive Masse nicht viel mit der Masse des freien Elektrons zu tun hat: Die
Krümmung der Dispersionskurve ist im wesentlichen durch das periodische
Potential bestimmt und nicht durch die Masse des freien Elektrons.
“leicht”, positiv
negativ
“schwer”, positiv
“normal”

Elektronen, die näher beim Atomkern sind, spüren ein stärkeres Potential, sie
werden schwerer. Die Bänder sind weniger aufgespalten, d.h. die effektive Masse
der Elektronen ist gross.
75887259
138
5/14/2016
3s
2p
2s
1s
klein
Kristall



Atomabstand
gross
freie Atome
Der Tensor 2. Stufe kann diagonalisiert werden und ist deshalb durch drei
Hauptmassen vollständig bestimmt.
Die Beschleunigung hat im allgemeinen eine andere Richtung als die
beschleunigende Kraft.
Der Tensor hängt von k ab.
Frage: Wie misst man die Masse der Elektronen: Durch Anlegen von Feldern
F  (m* ) ij a  k
k  eE(r , t )  v n (k )  B(r, t )  .
4.16. Elektrische Felder
Für elektrische Felder erhält man die Bewegungsgleichung für den Kristallimpuls:
k  eE(r ,t ) .
Die Fermikugel wird in k-Richtung mit einer Impulsänderung verschoben die
proportional zur Zeit ist (siehe früher in der Vorlesung).
k
k
75887259
139
5/14/2016
Wenn die Fermikugel die Brillouinzonengrenze überschreitet, wird sie zurückgefaltet
(siehe blaue Kugel). Die Elektronen werden nur solange beschleunigt, bis sie an einem
Gitterfehler ( Restwiderstand) oder Anregungen (z.B. Phononen) gestreut werden.
Typische Werte für Metalle sind:   10 14 s, was einer mittleren freien Weglänge
  20 nm entspricht (vergleiche: v F  1.4  10 6 m/s ). Durch die Streuung wird die
beschleunigende Wirkung des elektrischen Feldes kompensiert und es stellt sich im
Mittel eine konstante Verschiebung der Fermikugel ein:
k 
eE
.

Wir verwenden hier der Einfachheit halber ein ein-dimensionales Modell. Für die mittlere
Geschwindigkeit ergibt sich
k eE
v  *  * .
m
m
Wenn die Elektronen schwer sind, bewegen sie sich langsamer. Die folgende Figur zeigt,
dass der mittlere Impuls k x  0 wird. Beachte, dass k x nur  2  10 2 cm -1 ist für eine
Stromdichte von 100 Acm-2. Ein typischer Zonendurchmesser beträgt  2  10 8 cm -1 !
Metall
Ef
Für einen Isolator sind die Bänder gefüllt, d.h. die Elektronen am Zonenrand gelangen
direkt in die 2. BZ. und können in die 1. BZ zurückgefaltet werden. Die mittlere
Geschwindigkeit der Elektronen bleibt Null und es findet kein Beitrag zur Leitfähigkeit
statt.
75887259
140
5/14/2016
Isolator
Ef
Aufgrund von früher erhalten wir für die Leitfähigkeit:
 
e 2
n.
m*
Im Experiment können normalerweise nicht so hohe E-Felder angelegt werden (beim
Metall: Kurzschluss), dass man die Geometrie der Fermikugel messen kann. Eine
Ausnahme bildet der anomale Skineffekt bei sehr tiefen
Temperaturen: Wenn die freie Weglänge viel grösser als die
Eindringtiefe des elektromagnetischen Feldes ist, sind die
Elektronen, die zur Leitfähigkeit beitragen, einem
engbegrenzten Teil der Fermifläche zuzuordnen (A. B.
Pippard, Proc. Roy. Soc. A 191, 385 (1947)). Pippard gelang es
damit, die Fermifläche von Kupfer zu ermitteln.
Analog erhält man für die (elektronische) thermische Leitfähigkeit den modifizierten
Ausdruck
 2 2 n
E 
k BT * .
3
m
Das Wiedemann-Franz Gesetz gilt auch für Elektronen im schwachen Potential
L
 2  kB 
2
 
3  e 
da sich die effektiven Massen wegkürzen.
75887259
141
5/14/2016
4.17. Magnetische Felder
Ein äusseres Magnetfeld wirkt auf die Elektronen über die Lorentz-Kraft
k  ev n (k)  B(r, t )

e
k   * k  B ,
m
Wobei wir die Beziehung v  k / m * benutzt haben (beachte, m * ist ein Tensor). Die
Impulsänderung ist senkrecht zu k und B (siehe Figur). Da die Geschwindigkeit der
Elektronen immer senkrecht zu den Flächen konstanter Energie ist, wirkt die LorentzKraft tangential zu den Flächen konstanter Energie. Damit verlaufen die
Elektronenbahnen auf Flächen konstanter Energie.
 2r
r
 ev n  B  e  B .
2
t
t
Analog gilt im Ortsraum:
F  (m * ) ij
Durch Integration:
r
e
  * rB.
t
(m ) ij
Die Lösungen sind Kreisbahnen im Ortsraum. Sowohl im k- als auch im Ortsraum ergibt
sich für die Elektronen in einem Magnetfeld B  (0,0, B) eine Zyklotronfrequenz
c 
eB
,
m*
75887259
142
5/14/2016
wobei wir m*  (m* ) ij gesetzt haben. Es ist klar, dass für  c  1 (schwache
Magnetfelder, hohe Temperaturen) die Elektronen so rasch gestreut werden, dass keine
vollständigen Kreisbahnen ausgeführt werden. Für hohe Magnetfelder und tiefe
Temperaturen (  c  1) beschreiben die Elektronen Kreisbahnen, die aufgrund der
Quantentheorie quantisiert sind (vergleiche 2-dimensionalen harmonischen Oszillator):


2
2 2
2
2
k

k

kz
x
y
2m *
2m *
B  0:
E (k )  E  
B 0:

2 2 
E  E   (l  12 ) c 
k z   E  E  E||  .
2m* 

Hier bezeichnet E die Energie des Bandrandes und l  0,1,2,... die Landau’sche
Quantenzahl, die die diskreten Elektronenbahnen als neue Energiezustände des
Elektronengases quantisiert. Die Flächen E  const sind Zylinderflächen. In einem
Magnetfeld werden die besetzten Zustände innerhalb der Fermikugel auf Zylinderflächen
2m * c
2eB
mit den Radien k 2 
(l  12 ) 
(l  12 ) umverteilt.


Die linke Figur zeigt die Aufspaltung eines Energiebandes im Magnetfeld für Richtungen
parallel ( k || ) und senkrecht ( k  ) zu Bz . Die rechte Figur zeigt Flächen konstanter
Energie für Bz  0 und Bz  0 .
Im folgenden betrachten wir ein System mit einer isotropen, effektiven Masse m * und
setzen E  0 . Für B  0 erhalten wir für die Zustandsdichte
75887259
143
5/14/2016
3
L3
D( E )dE 
(2 ) 2
 2m*  2 12
 2  E dE .
  
Für B  0 kondensieren die Zustände auf die Zylinder E  (l  12 ) c  const , d.h. es
sind nur noch gewisse Transversalenergien E  erlaubt. Analog zum Gas der freien
Elektronen erhält man für die Zustandsdichte
L
D( E , k z )dE dk z  
 2
3

 2 k  dk  dk z .

Die Übungsaufgabe (siehe Serie 16) zeigt, dass die Zahl der Zustände auf allen Bahnen
mit verschiedenen l gleich ist und gegeben ist durch
3
L  2m *  2  c


D(l , E )dE 
(2 ) 2   2  2
3


 1
 E   l  2  c 





1
2
dE .
Jedes Landauniveau trägt zur Zustandsdichte wie ein ein-dimensionales Elektronengas
bei, i.e. D  1 / E . Für die totale Zustandsdichte muss man über alle Teilbänder l
summieren, für die die Wurzel positiv bleibt
l
D( E )dE   D(l , E )dE .
l 0
In der folgenden Figur ist der Verlauf der Zustandsdichten für ein Valenz- und ein
Leitungsband gezeigt. Beachte, dass die Zustandsdichte an jedem Teilbandrand unendlich
ist und dass die Aufspaltung der Energieniveaus infolge des Elektronenspins nicht
berücksichtigt ist.
75887259
144
5/14/2016
Das Magnetfeld bewirkt eine grundlegende Änderung der Bandstruktur. Solange aber die
Magnetfelder nicht zu gross sind, liefern Messungen einer physikalischen Grösse in
Funktion der Kristallorientierung wichtige Informationen über die Querschnitte der
Energieflächen.