7.5 Lageparameter: Mittelwert, Median, Modus

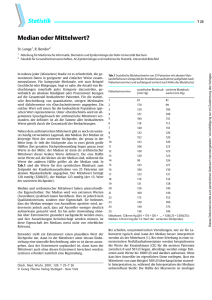
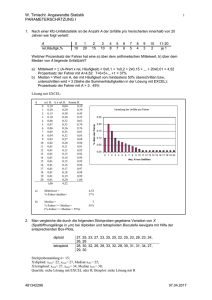
7.5 Lageparameter: Mittelwert, Median, Modus
In nahezu jeder Studie ist es erforderlich, die gewonnenen Daten in geeigneter und
einfacher Weise zusammenzufassen. Für die statistische Beschreibung von
quantitativen, stetigen Merkmalen wird üblicherweise ein "Durchschnittswert"
angegeben. Ein solcher Wert soll einen für die beobachtete Population typischen
Wert repräsentieren. Durchschnittswerte werden gelegentlich auch Lageparameter
bezeichnet, weil er die Lage des Mittels auf einer Merkmalsachse bezeichnen. Zur
Auswahl stehen der Modus, der Median und der arithmetische Mittelwert.
Ein häufig verwendetes Lagemaß ist der Median. Der Median ist derjenige Wert der
sortierten Stichprobe, der genau in der Mitte liegt. Er teilt die Stichprobe also in zwei
gleich große Hälften (bei geradem Stichprobenumfang liegen genau zwei Werte in
der Mitte; der Median ist dann als arithmetischer Mittelwert dieser beiden Werte
definiert).Die eine Hälfte weist Werte auf, die kleiner als der Median sind, während
die Werte der anderen Hälfte größer als der Median sind.
Beispiel
1 3 5 7 9 11 13
Der mittlere Wert ist die 7, 7 ist also der Median. Diese einfache Bestimmung
kann nur dann angewandt werden, wenn die Anzahl der Messungen ungerade.
Beispiel
Ein Sonderfall liegt dann vor, wen die Anzahl der Messungen gerade ist
1 3 5 7 9 11
In diesem Fall wird der arithmetische Mittelwert aus den beiden mittleren
Messungen gezogen, 5+7= 12:2=6.
Eine positive Eigenschaft des Medians besteht darin, das er weniger anfällig für
Verzerrungen durch Extremwerte, Ausreißer oder "schiefe Verteilungen" ist.
Beispiel:
1 3 5 7 9 11 53
Der mittlere Wert/Median beträgt 7.
Beispiel
Ein typisches Beispiel ist die Verteilung des Einkommens.
100 Personen verdienen 1000 Euro, 100 Personen verdienen 2000 Euro, 100
Personen verdienen 3000 Euro und eine Person verdient 1.400.000 Euro. Das
arithmetische Durchschnittseinkommen beträgt 2.000.000: 301=6644,5 Euro.
Der Median von 301 Messungen liegt bei Messung 150=2.000 Euro.
Das arithmetische Mittel ist als 6644 Euro, liegt weit über dem, was 99,6
Prozent der Befragten tatsächlich verdienen und ist das Resultat eines
einzelnen Extremwertes. Es taugt also nicht als Mittelwert, der ja einen
typischen Wert ausdrücken soll. Der Median ist da weitaus besser geeignet.
Neben dem Median wird gelegentlich auch noch auf die Messung verwiesen, die am
häufigsten vorkommt, der also am wahrscheinlichsten ist. Dies ist der so genannte
Modus oder Modalwert. Der Modalwert ist der wahrscheinlichste Wert, da er am
häufigsten vorkommt. Er dient vor allem dazu „Normalität und Regelmäßigkeit“
auszudrücken (Wagschal, 1999: 96).
Beispiel:
100 Personen verdienen 1000 Euro, 10 Personen verdienen 2000 Euro und 1
Person verdient 3000 Euro, so beträgt der Modus 1000 Euro.
Am geläufigsten dürfte jedoch der Mittelwert sein, oder genauer der arithmetische
Mittelwert sein, der allgemein auch der „Durchschnitt“ genannt wird. Er ist definiert ist
als die Summe aller beobachteten Werte geteilt durch die Gesamtzahl der
Beobachtungen.
Beispiel:
1 3 5 7 9 11
Summe 36 dividiert durch Anzahl der Messungen, 6, macht 6. 6 ist also der
arithmetische Mittelwert.
Eine negative Eigenschaft des arithmetischen Mittelwertes besteht darin, das er
durch Extremwerte enorm verzerrt wir.
Beispiel
1 3 5 7 9 53
Summe 78, dividiert durch 6, macht 18. Der Mittelwert wird also durch einen
sogenannten Ausreißer stark beeinflusst. Er ist nicht repräsentativ für die
Messung und deshalb unbrauchbar
Es wird allerdings zwischen zwei Arten von Mittelwerten unterschieden, dem
gewogenen und dem ungewogenen arithmetischen Mittel. Die bisherigen Beispiele
illustrieren den ungewogenen arithmetischen Mittelwert, dessen Berechnung basiert
auf relativ simplen Formeln.
Der gewogene Mittelwert empfiehlt sich demgegenüber in Fällen, in denen der
Messgegenstand komplexer ist und beispielsweise je Wert mehrere Personen
beinhaltet.
Beispiel
Ausländer pro Wohnhaus
Ausländer/Wohnhaus Absolute
xi
Häufigkeit
ni
Relative
Häufigkeit
hi
Gewichtung mit
absoluter
Häufigkeit
xi mal n
24
156
165
88
85
24
542
Gewichtung mit
relativer
Häufigkeit
xi mal hi
0.12
0.78
0.825
0.44
0.425
0.12
Σ 2.71
1
24
0.12
2
78
0.39
3
55
0.275
4
22
0.11
5
17
0.085
6
4
0.02
Summe/Mittelwert
200
1.0
Glossar:
Absolute Häufigkeit: Anzahl der Fälle/Vorkommen
Relative Häufigkeit: Anteil der Fälle bezogen auf die Grundgesamtheit 1
Gewichtung mit absoluter Häufigkeit: Anzahl der Fälle multipliziert mit der Anzahl der Personen
je Fall.
Gewichtung mit relativer Häufigkeit:: Anzahl der Fälle multipliziert mit der Anzahl der relativen
Personenfall je Fall.
Bei jeder Anwendung muss gesondert über Extremwerte nachgedacht und ihre
Auswirkungen berücksichtigt werden. Entweder stellt ein Extremwert einen plausiblen
Wert der Stichprobe dar, dann kann der Mittelwert unter dessen Einbeziehung eine
sinnvolle Beschreibung sein, oder es ist davon auszugehen, dass der Extremwert
nicht plausibel ist, etwa weil er auf Störungen oder Fehlmessungen beruhen könnte,
dann kann der Mittelwert auch ohne diesen Extremwert berechnet werden. Dies
muss aber begründet werden.
Streuung, Standardabweichung, Varianz
Die Streuung (s) gibt an, wie weit die Messungen auseinander liegen.
Beispielsweise lassen im Fall der Einkommensverteilung weder das arithmetische
Mittel noch der Median auf den Extremwert schließen. In diesem Fall würde man
zusätzlich die Spannbreite angeben, die Differenz zwischen dem Minimum und dem
Maximum.
Beispiel:
2.000.000 - 1.000=1.900.000 Euro.
Alternativ lässt sich die Spannbreite aber auch dadurch darlegen, das schlichtweg
die Minimal- bzw. Maximalwerte genannt werden. das also gesagt wird, die
Einkommen liegt zwischen 1000 Euro und 2.000.000 Euro.
Da die Spannbreite aber nichts über die Häufigkeit aussagt und deshalb oft wenig
aussagekräftig ist, wird deshalb die Häufigkeit, d.h. die Verteilung anhand von Einer-,
Zehner oder Viertelschritten dargestellt, den so genannten Quantilen, Dezilen oder
Quartilen. Anhand der Quartilen lässt sich ausdrücken, das 99,6 Prozent der Fälle
kleiner sind, als der arithmetisch errechnete Mittelwert.
Anhand der Streuung lassen sich Mittelwerte miteinander vergleichen. Nur anhand
der Angabe der Streuung lässt sich erkennen, dass gleiche Mittelwerte dennoch auf
ungleiche Verhältnisse hinweisen, weil sie auf einer ungleichen Streuung basieren.
Beispiel
1: Einkommen: Person 1: 0; 2: 6000; 3: 12.000; 4: 12.000; 5: 22.000
M=10.400, s=22.000
2: Einkommen: Person 1: 2000; 2: 5000; 3: 10.000; 4: 15.000; 5: 20.000
M=10.400, s=18.000
3: Einkommen: Person 1: 8.000; 2: 9.000; 3: 10.000; 4: 12.000; 5: 13.000
M=10.400, s=5.000
Insbesondere Fall 1 und Fall 3 im Vergleich zeigen auf, das trotz gleicher Mittelwerte
zwei gänzlich verschiedene Fälle vorliegen, Fall 1 weist auf eine sehr heterogene
Gruppe, Fall 3 auf eine eher homogene Gruppe hin.
Die Standardabweichung (S, SD [standard deviance], mittlerer Fehler) ist ein Maß für
die Streuung um einen Mittelwert herum.
Sie wird wie folgt berechnet:
1. Zunächst wird das arithmetische Mittel (x) der Messwerte berechnet.
2. Für jeden Messwert wird die Differenz zwischen ihm und dem AM berechnet
(1. Messwert minus x; 2. Messwert minus x, ...). Daraus ergeben sich so
viele Differenzen, wie es Messwerte gab.
3. Alle Differenzen werden (einzeln) quadriert.
4. Die Summe der quadrierten Differenzen, die Quadratsumme, wird errechnet.
5. Die Summe wird durch die Anzahl der Messwerte (= der Anzahl der
Differenzen) dividiert, (bei schließender Statistik durch die Anzahl der Werte
minus 1).
6. Aus dem Ergebnis aus 5. wird die Wurzel gezogen.
Beispiel
Dies soll am Fall 2, siehe oben, vorgeführt werden.
2000-10.400=-8.4002=70.560.000 usw.
(70.560.000+ 29.1600.000 + 160.000 + 21.160.000 + 92.160.000) durch 5,
daraus die Wurzel √ 0 1252.0639 S. Dies ist ein relativer Wert mit geringer
sachlogischer Bedeutung.
Die Varianz ist ein weiteres Maß für die Streuung einer Verteilung in Form des
Quadrates der Streuung.