Reales Gas

Zustandsgleichungen (Equations of State – EOS)
Ein einfaches Beispiel:
Eisen hat unter Normalbedingungen einen Kompressionsmodul von K=173 GPa
Wenn das lineare Hookesche Gesetz bis ins Erdzentrum gelten würde,
 (V(P) –V(P=0))/V(P=0) = -P/K d.h. V(P=350 GPa) = Vo (1 – 350/173) ~ -Vo
d.h. Eisen wäre im Zentrum völlig zusammengequetscht, wenn die lineare
Elastizitätstheorie weiter gelten würde!
Selbst Diamant mit einem Kompressionsmodul von K = 585 GPa würde auf 0.4 Vo
zusammengedrückt werden.
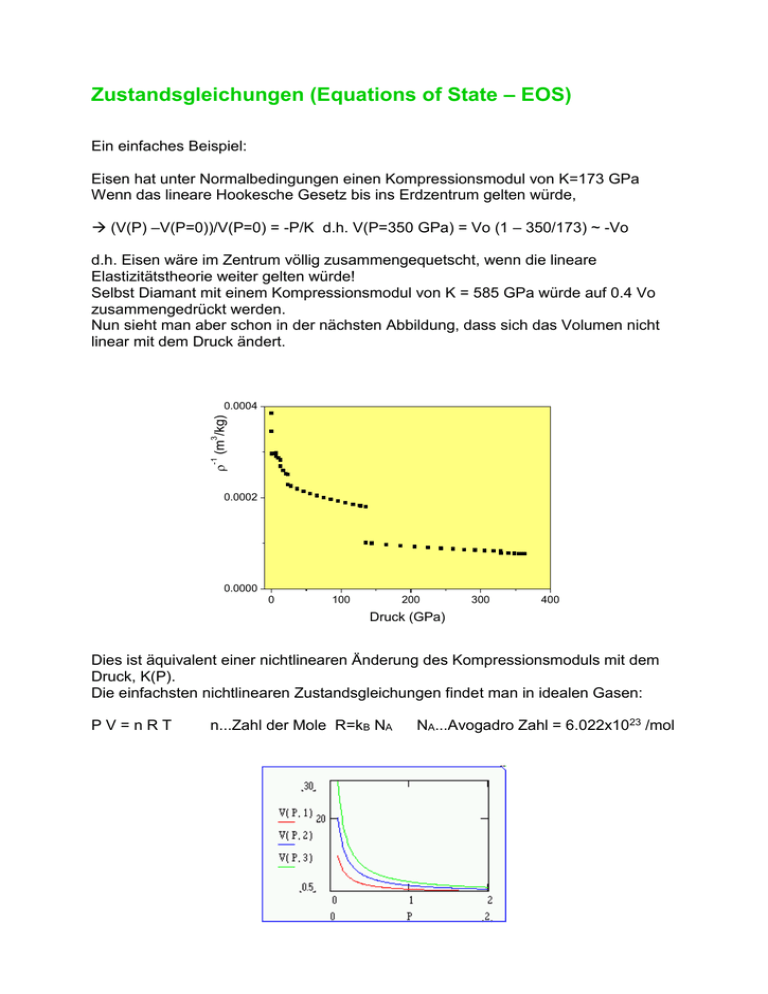
Nun sieht man aber schon in der nächsten Abbildung, dass sich das Volumen nicht
linear mit dem Druck ändert.
-1
3
 (m /kg)
0.0004
0.0002
0.0000
0
100
200
300
400
Druck (GPa)
Dies ist äquivalent einer nichtlinearen Änderung des Kompressionsmoduls mit dem
Druck, K(P).
Die einfachsten nichtlinearen Zustandsgleichungen findet man in idealen Gasen:
PV=nRT
n...Zahl der Mole R=kB NA
NA...Avogadro Zahl = 6.022x1023 /mol
Die obige Abbildung zeigt V(P) = n.R.T/P für verschiedene Temperaturen, d.h. K(P)
ist für eine ideales Gas gegeben durch:
K=-V dP/dV = P
damit wird die Schallgeschwindigkeit zu vs = (P/)1/2
Bemerkung: Genau genommen muss man in obiger Gleichung noch den Unterschied
von adiabatischer und isothermer Schallausbreitung berücksichtigen. Dann gilt:
vs = ( P/)1/2 wobei  der sogenannte Adiabatenexponent ist.
Er ist gegeben durch das Verhältnis der spezifischen Wärmen Cv und Cp, bei
konstantem Volumen und konstantem Druck, i.e.  = Cp/ Cv = (f+2)/f
wobei f = Zahl der Freiheitsgrade der Gasteilchen.
Für ein einatomiges Gas (zB He) f=3 (3 Translationsfreiheitsgrade)  ~1.7
Für Luft, die hauptsächlich aus N2 und O2 besteht (siehe Tabelle) ist f=5 (3
Translations und 2 Rotationsfreiheitsgrade der 2-atomigen Gasmoleküle)  ~1.4
Der tatsächliche Wert von Luft ist =1.402.
Die Schallgeschwindigkeit von Luft ist Vs= 343 m/s bei 20°C Temperatur.
Bei höherer Temperatur steigt die Schallgeschwindigkeit nach dem Gesetz:
Vs = (1.402 R T / 0.02896)1/2
Das ist anders als in Festkörpern, wo die Schallgeschwindigkeit im allgemeinen mit
zunehmender Temperatur abnimmt.
Die Dichte  steigt linear mit P, d.h.  ~ P/T
Bemerkung: Der Unterschied von isothermer und adiabatischer Schallausbreitung
spielt auch eine große Rolle in Festkörpern, insbesondere im Inneren unserer Erde.
Mehr dazu später.
Reales Gas
Reale Gase werden durch die sogenannte Van der Waals-Gleichung beschrieben.
(P + a/V2)(V-b) = NA kB T
wobei „b“ das Eigenvolumen der Atome berücksichtigt und „a“ berücksichtigt die
gegenseitige Anziehung der Atome.
 P(V) = NA kB T/(V-b) – a/V2
Verschiedene nichtlineare Druckabhängigkeiten des Volumens V(P) für
Festkörper
1. Die einfachste Näherung
Betrachte K = - V dP/dV als Differentialgleichung
Lösung durch „Trennung der Variablen“
dV/dP = - V/K  V(P) = V(P=0) e –P/K
“simple Equation of State“
Reihenentwicklung von V(P) liefert: V(P)=Vo (1 – P/K + ½ P2/K2 -....)
In diesem Fall hängt K nicht von P ab!
Beispiel: Verhalten von Eisen (K=173 GPa, rote Kurve) und Diamant (K=585 GPa,
blaue Kurve) mit dieser Zustandsgleichung. Man sieht, dass Eisen im Erdzentrum
auf etwa 20% des Volumens komprimiert wäre, wenn es dieser einfachen
Zustandsgleichung gehorchen würde. Bei Diamant wären es etwa 60%.
Tatsächlich wird Eisen nur auf etwa 60% des Volumens komprimiert (vgl. unter
Normalbedingungen lautet =7.87 g/cm3 und im Erdinneren =13.08 g/cm3 ).
2. die nächst einfache Näherung
Man entwickelt den Kompressionsmodul in eine Reihe
K(P) = K(P=0) + dK/dP(P=0) P = Ko + K’ P
d.h. das Material reagiert „härter“ bei erhöhtem Druck!
Damit lautet die Gleichung für den Kompressionsmodul
Ko + K’ P = -V dP/dV
„Trennung der Variablen“
(Ko + K’ P)/dP = - V/dV
Integration auf beiden Seiten liefert
- 1/K’ ln(1 + P K’/Ko) = ln V 
V(P) = V(P=0) [1 + P K’/Ko]-1/K’
„Lineare Murnaghan EOS“
oder P(V) = Ko/K’ [(Vo/V)K’ – 1]
In vielen dichtgepackten Mineralien ist K’~4
z.B. MgO (4.1), CaO (4.2), Mg2GeO4 (Spinel, 4.1), MgSiO3 (Perovskit, 3.9)
Die nachfolgende Zeichnung zeigt wieder das Druckverhalten von Eisen (rote Linie)
und Diamant (grüne Linie) diesmal unter der Annahme von „Murnaghan linear EOS“
mit K’=4. Die punktierte Linie zeigt den Vergleich von Eisen mit „simple EOS“.
Die lineare „Murnaghan EOS“ beschreibt den tatsächlichen Verlauf von Eisen schon
ganz gut, aber noch nicht perfekt (siehe später genaueres...).
Wie das nächste Bild zeigt, ist MgO ein Material, welches sich sehr gut mit der
linearen Murnaghan Zustandsgleichung mit K’=4.56 beschreiben lässt.
Auch für den unteren Erdmantel und für den äußeren Kern hat man typisches
„Murnaghan“ Verhalten für den adiabatischen Kompressionsmodul gefunden:
unterer Erdmantel KS = 229 + 3.16 P (GPa)
äußerer Kern
KS = 184 + 3.44 P (GPa)
2te Ordnung Birch-Murnaghan EOS
P(V) = 3 Ko/2 [(Vo/V)7/3 - (Vo/V)5/3]
 K() = dP/dln = Ko/2 [7(/o)7/3 - 5(/o)5/3]
Der Ursprung für die 2te Ordnung Birch-Murnaghan Gleichung liegt in der Tatsache,
dass bei hohen Drücken die Verzerrungen (Strains) nicht mehr als infinitesimal klein
angenommen werden können.
Die Strains schreibt man ja üblicherweise als:
ij = ½ (dui/dxj + duj/dxi) – ½ k duk/dxi duk/dxj
in der infinitesimalen Näherung vernachlässigt man den zweiten Term.
Diese Näherung geht jedoch nur solange gut, solange die Strains in der
Prozentgegend liegen. Bei hohen Drucken erreicht man aber leicht Verzerrungen in
der „zig-Prozentgegend“.
Die 2te Ordnung Birch-Murnaghen EOS verwendet man bis etwa 10 GPa Druck.
in vielen dichtgepackten Mineralien ist K’=4
MgO
CaO
Mg2 GeO4
Mg2 SiO4
Fe2 SiO4
MgSiO3
4.1
4.2
(spinel)
4.1
(forsterite)
4
(fayalite)
5.2
(perovskite) 3.9
3te Ordnung Birch-Murnaghan EOS
P(V) = 3 Ko/2 [(Vo/V)7/3 - (Vo/V)5/3]{1 + ¾(K’-4)[(Vo/V)2/3 –1]}
Für K’=4 erhält man die 2te Ordnung Birch-Murnaghan Gleichung.
Die 3te Ordnung Birch-Murnaghan Gleichung wird bis etwa 100 GPa verwendet.
Beispiel: EOS von Gold gefittet mit K’~5 (Earth
and Planetary Science Letters 203 (2002) 729 -739)
Für verschiedene Anziehungs-bzw. Abstossungsterme im Potential E(V) kann man
Birch-Murnaghan artige Zustandsgleichungen bekommen.
E = -a V-m/3 + b V-n/3
(*)
Für Van-der Waals Wechselwirkung der Edelgase m=6, n=12, denn
E(r)=4 [-(/r)6 + (/r)12]
Gleichung (*) liefert P=-dE/dV = -ma/3 V(-m/3 + 1) + nb/3 V(-n/3 + 1)
K = -V dP/dV = -ma/3 (m/3+1) V(-m/3 + 1) + nb/3 (n/3+1) V(-n/3 + 1)
für P=0, K=Ko , V=Vo  a=9Ko/m(n-m) Vo(m/3+1)
b= 9Ko/m(n-m) Vo(n/3+1)
 P = 3Ko/(n-m) [(Vo/V)(n/3+1) - (Vo/V)(m/3+1)]
K(V) = Ko/(n-m) [(n+3)(Vo/V)(n/3+1) – (m+3)(Vo/V)(m/3+1)]
K’ = (dK/dP)P=0 = 1/3 (m+n+6)
Vergleich: 2te Ordnung Birch-Murnaghan EOS
K(V) = Ko/2 [7(Vo/V)7/3 – 5(Vo/V)5/3]
n/3+1=7/3  n=4
m/3+1=5/3  m=2
K’ = 1/3(2+4+6)=4
Für Edelgase (d.h. mit Van der Waals Wechselwirkung) gilt
K(V) = Ko/2 [5(Vo/V)5 –3(Vo/V)3]
K’ = 1/3(6+12+6) = 8
Wie wählt man die beste Zustandsgleichung für ein bestimmtes Material?
Für grobe Näherungen ist die Murnaghan EOS sehr nützlich, da sie sehr einfach ist.
Immer dann wenn der Druck kleiner als etwa Ko/3 ist, geben alle
Zustandsgleichungen dasselbe Resultat.
Die sogenannten Born-Mie und Born-Meyer EOS sind sehr nützlich, da man sie in
Verbindung mit den Scherkonstanten unter hohem Druck bringen kann.
Die Birch-Murnaghan Gleichung hat sich als gut herausgestellt für Materialien, die
3.4 < K’ < 7 haben. Das gilt zum Glück für die meisten Mineralien im Erdinneren (mit
Ausnahme von orthopyroxene).
Für Flüssigkeiten, bei denen K’ meist größer als 7 ist kann die Birch-Murnaghan
EOS nicht verwendet werden, da verwendet man dann oft die sogenannte
Vinet-Gleichung
P(V) = Ko (V/Vo)-2/3 [1- (V/Vo)-1/3] exp[3/2 (K’-1)(1-(V/Vo)-1/3)]
Der Vollständigkeit halber wollen wir noch die „Thomas Fermi“ Zustandsgleichung
besprechen:
Man nimmt an, dass der Druck nur durch ein degeneriertes Elektronengas entsteht
und vernachlässigt komplett die atomare Struktur des Festkörpers. Dies gilt streng
nur für höchste Drücke (> 1000 GPa), wie sie z.B. im Inneren von Sternen
vorkommen. Eigentlich ist diese Zustandsgleichung nicht für geophysikalische
Probleme anwendbar. Sie wurde aber in der Literatur verwendet um zwischen
„Murnaghan-EOS“ und „Thomas-Fermi-EOS“ zu interpolieren, und so etwas über den
Eisenkern herauszufinden (siehe nächste Abbildung).
Thomas Fermi Näherung
Sie beruht auf folgenden Annahmen:
- System ist im niedrigsten Quantenzustand
- Elektronen bilden ein Elektronengas
- Festkörper wird als Gas von Atomen aufgefasst, der Druck entsteht durch das
Bombardement der freien Elektronen am Rand der Atome, die kugelförmig
angenommen werden  „kinetische Gastheorie“
In der kinetischen Gastheorie ist der Druck gegeben durch: P = 1/3 n m v2, wobei
n=N/V die Zahl der Moleküle pro Volumseinheit ist und m die Masse.
d.h. P V = 2/3 mv2/2 = 2/3 Ekin
oder P = 2/3 Ekin/N n
die kinetische Energie pro Elektron Ekin/N = h2/2m kF2
da kF = (3 2 N/V)1/3  P = 2/3 h2/2m (3 2 n)2/3 n 
P = 2/3 h2/2m (32)2/3 Z5/3 V-5/3
Thomas-Fermi EOS
Brillouin hat 1954 den elektronischen Druck von Metallen unter der Annahme eines
freien Elektrons pro Atom mit ca. 10 GPa abgeschätzt.
Thermische Zustandsgleichungen
Bis jetzt haben wir uns mit isothermen Zustandsgleichungen beschäftigt, d.h. EOS
bei Raumtemperatur. Nun wollen wir die Temperaturabhängigkeit der EOS
berücksichtigen.
Man kann den thermischen Druck Pth schreiben als:
T
T
Pth = (P/T)V dT =  KT dT
0
0
wobei  = V/T der Volumsexpansionskoeffizient ist.
Wenn man annimmt, dass  KT konstant, d.h. unabhängig von der Temperatur ist, für
T> (Debyetemperatur) – eine Annahme, die in den meisten Fällen zutrifft 

Pth =  KT dT
0
+  KT (T-)
Diese lineare Beziehung für den thermischen Druck ist für die meisten Materialien
sehr gut erfüllt (siehe nächste Abbildung).
Experimentell bestimmter thermischer Druck (relativ zum thermischen Druck bei
Raumtemperatur) vs. T/
Der thermische Druck im Mantel