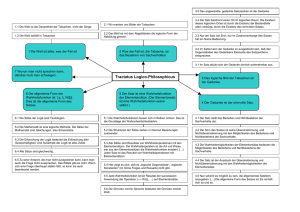
Baumkalkül für PL - UK

19. Logische Wahrheit in der PL
Wie in der AL können wir für die Sätze der PL präzise angeben, was unter einer „logischen
Wahrheit“ und einer „logischen Folgerung“ zu verstehen ist. Beide Begriffe werden ganz
analog zur AL definiert, allerdings mit dem Unterschied, dass wir anstatt der Bewertungen V
jetzt die Interpretationen I variieren. Das liefert die folgenden beiden Definitionen:
Definition: Logische Wahrheit in PL
Ein Satz A der Sprache PL ist genau dann logisch wahr, wenn er unter allen Interpretationen I
wahr ist. Für die Aussage, dass A logisch wahr in PL ist, schreiben wir kurz: PL A.
(Sofern klar ist, dass wir uns dabei auf PL beziehen, kann der Index auch wegfallen.)
Definition: Logische Folgerung in PL
Seien A1,..., An Sätze der Sprache PL. Dann folgt der Satz An logisch aus den Sätzen A1, ..,
An-1 genau dann, wenn An unter allen Interpretationen I, unter denen die Sätze A1, ..., An-1
wahr sind, ebenfalls wahr ist. Wir schreiben dafür: A1, ..., An-1 PL An.
Bem.: Wenn zwei Sätze A und B von PL jeweils logisch auseinander folgen, d.h. wenn
sowohl A PL B als auch B PL A gilt, so nennt man A und B logisch äquivalent. Wir
schreiben kurz: A   PL
Unentscheidbarkeit der PL
Wie steht es mit dem Beweisen der logischen Wahrheit und der logischen Folgerung in PL?
In der Prädikatenlogik zeigt es sich leider – im Unterschied zur Aussagenlogik –, dass es mit
einem allgemeinen Beweisverfahren, das man auf beliebige vorgegebene Sätze anwenden
kann, nicht so günstig steht. Ein solches allgemeines Beweisverfahren gibt es für PL nicht.
Genauer gesagt lautet dieses negative Ergebnis folgendermaßen:
Unentscheidbarkeit der PL
Die Sätze der PL sind nicht entscheidbar, d.h.: Es gibt kein allgemeines Verfahren, das für
beliebige Sätze der PL nach endlich vielen Schritten das Ergebnis ‚logisch wahr‘ oder das
Ergebnis ‚nicht logisch wahr‘ liefert.
1
Die Beweisverfahren, die man kennt, sind nämlich entweder nicht so allgemein, dass sie für
jeden beliebigen Satz zu einem solchen Ergebnis führen, d.h. entscheiden, ob er logisch wahr
ist oder nicht (sie funktionieren also nur für manche Sätze, nicht für alle); oder sie brechen für
manche Sätze nicht nach endlich vielen Schritten ab (so dass man nie an ein Ende kommt).
Die logische Wahrheit in der PL kann also nicht mechanisch entschieden werden. Man muss
für jeden Satz nach einem Beweis suchen.
Trotz dieses negativen Resultats für die PL lassen sich natürlich einzelne Sätze in der PL als
logisch wahr nachweisen, und es lässt sich auch für manche Formen von Sätzen in der PL
nachweisen, dass jede Instanz der entsprechenden Form eine logische Wahrheit ist. Wichtige
logische Wahrheiten bzw. logische Folgerungen liefern die folgenden beiden Sätze:
Satz:
Wenn A und B Satzfunktionen in PL sind, in denen nur die Individuenvariable  frei
vorkommt, dann gilt:
1.
A PL A
2.
A PL A
3.
A PL A
4.
A PL A
5.
PL (AB) (AB)
6.
PL (AB)(AB)
(Die ersten vier Formeln sollte man sich unbedingt merken, da sie im Baumkalkül
Verwendung finden.)
Beispiele:
(1)
xFx xFx
1, 4
(2)
yRya    yRya
2, 3
2
Satz:
Wenn A eine Satzfunktion ist, in der nur die Individuenvariable  frei vorkommt, und  eine
beliebige Individuenkonstante, dann gilt:
1.

A  A
2.

A  A
Beispiele:
(1)

xFx  Fa
(2)

yxRyx  xRcx
(3)

Fa  xFx
Prädikatenlogik: Der Baumkalkül
Der Baumkalkül kann auch für die PL verwendet werden. Dort führt er zwar nicht immer zu
einem Ergebnis (wegen der Unentscheidbarkeit der PL), aber oft eben doch. Die Methode des
Baumkalküls ist wiederum von der Idee her dieselbe wie in der Aussagenlogik, d.h. sie beruht
auf einem indirekten Beweis (durch Widerspruch). Aus der Annahme, dass ein vorgegebener
Satz keine logische Wahrheit ist, wird ein Widerspruch abgeleitet; und damit kann man
schließen, dass der ursprüngliche Satz eine logische Wahrheit ist. Nur: Es gelingt eben nicht
immer, einen solchen Widerspruch abzuleiten – und zwar auch manchmal nicht für Sätze, die
tatsächlich logisch wahr sind. In dem Fall, dass man keinen Widerspruch ableiten kann, kann
man daher nicht schließen, dass der Satz keine logische Wahrheit ist (wie man in der AL
schließen konnte). Man kann einfach (zunächst) keine Aussage über seine logische Wahrheit
treffen. In diesem Fall kann man aber immer noch versuchen, durch die Angabe eines
Gegenbeispiels – d.h. einer Interpretation, die den Satz falsch macht – nachzuweisen, dass er
keine logische Wahrheit ist. (Auch dafür gibt es aber kein völlig allgemeines Verfahren.)
Wie konstruiert man ein Gegenbeispiel?
Wenn sich eine Interpretation der Individuenkonstanten und Prädikatsbuchstaben finden lässt,
die den gegebenen Satz falsch macht, dann handelt es sich nicht um eine logische Wahrheit.
Wir können dabei natürliche
Interpretationen betrachten, aber auch konstruierte
Interpretationen.
3
Beispiel 1: Fa  xFx
Natürliches Gegenbeispiel:
D = Menge der natürlichen Zahlen
V(a) = 7
V(F) = xx ist eine Primzahl
7 ist eine Primzahl, aber es gibt mindestens eine a-Variante von xFx, so dass Fa falsch ist
(mit V‘(a) = 4).
Konstruiertes Gegenbeispiel:
D = 1, 2
V(a) = 1
V(F) = 1
Ergebnis: (1) ist keine logische Wahrheit!
Beispiel 2: x(FxGx)  x(GxFx)
Gegenbeispiel:
D = die Menge der Lebewesen
V(F) = xx ist ein Hund
V(G) = xx ist ein Säugetier
Ergebnis: (2) ist keine logische Wahrheit!
Beispiel 3: xFx  xGx  x(FxGx)
Gegenbeipiel:
D = Menge der natürlichen Zahlen
V(F) = xx ist eine gerade Zahl
V(G) = xx ist eine ungerade Zahl
Ergebnis: (3) ist keine logische Wahrheit!
Im Folgenden werden wir den Baumkalkül für PL gleich als ein syntaktisches Verfahren
angeben, das allein durch die Anwendung einer bestimmten Menge von Regeln auf die Sätze
unter Absehung von deren Bedeutung funktioniert. (Dass diese Regeln auch die ‚richtigen‘
sind, kann bewiesen werden, ist aber auch ohne einen Beweis intuitiv einsehbar!)
4
Der Baumkalkül für PL ist eine Erweiterung des Baumkalküls von AL. Er umfasst also
zunächst dieselben Regeln wie das Baumkalkül von AL. Diese Regeln waren die folgenden:
A
(DN)
A
(K)
AB
A
B
(A)
AB
A
(S)
B
AB
A
(B)
B
AB
A
A
B
B
(AB)
(NK)
A
B
(AB)
(NA)
A
B
 (A  B)
(NS)
A
B
(AB)
(NB)
A
A
B
B
5
Der PL-Kalkül enthält nun zusätzlich vier weitere Regeln:
(U)
Wenn  eine beliebige Individuenkonstante ist:
A
A
(E)
Wenn  eine Individuenkonstante ist, die in dem betreffenden Zweig noch nicht
vorgekommen ist:
A
A
(NU) A
A
(NE) A
A
1. Beispiel
(1)
xFx  Fa
1.
(xFx  Fa)
A
2.
xFx
(1)
NS
3.
Fa
(1)
NS
4.
Fa
(2)
U
4x3
1. Trick:
Bei Anwendungen von (U) sollte man solche Individuenkonstanten wählen, die schon vorher
im Zweig vorgekommen sind.
2. Beispiel
(2)
xFx  xFx
1.
(xFx  xFx)
A
2.
xFx
(1)
NS
6
3.
xFx
(1)
NS
4.
xFx
(3)
NE
5.
Fa
(2)
U
6.
Fa
(4)
U
6x5
2. Trick:
Negierte quantifizierte Formeln zuerst entwickeln!
3. Beispiel:
(3)
x(FxGx)  (xFx  xGx)
Da die Wahl der Individuenkonstanten bei existenzquantifizierten Sätzen eingeschränkt ist
(Regel (E)), ist es günstiger, diese Regel anzuwenden, bevor man für allquantifizierte Sätze
Individuenkonstanten einsetzt (nach Regel (U)). Bei (U) kann man ja dann beliebige
Individuenkonstanten wählen – und wählt natürlich die, die (im betreffenden Zweig) bereits
vorgekommen sind.
1.
(x(FxGx)  (xFx  xGx))
A
2.
x(FxGx)
(1)
NS
3.
(xFx  xGx)
(1)
NS
4.
xFx
(3)
NS
5.
xGx
(3)
NS
6.
xGx
(5)
NU
7.
Ga
(6)
E
8.
Fa
(4)
U
9.
Fa  Ga
(2)
U
10.
Fa
(9)
S
10x8
11.
Ga
11x7
3. Trick:
Existenzquantifizierte Formeln vor allquantifizierten Formeln entwickeln!
7
4. Beispiel:
(4)
yxRxy  xyRxy
1.
(yxRxy  xyRxy)
A
2.
yxRxy
(1)
NS
3.
xyRxy
(1)
NS
4.
xyRxy
(3)
NE
5.
xRxa
(2)
U
6.
Rba
(5)
E
7.
yRby
(4)
U
8.
yRby
(7)
NU
(negierte quantifizierte F. zuerst!)
(neue Konstante!)
An dieser Stelle hätte man vielleicht gerne gesetzt:
9.
Rba
(8)
E
Das ist aber unzulässig, da man bei der Weiterentwicklung eines existenzquantifizierten
Satzes gemäß der Regel (E) für die betreffende Variable keine Konstante einsetzen darf, die
im betreffenden Zweig schon einmal vorkam – wie dies bei ‚a‘ hier eben der Fall ist. Man
muss eine neue Variable, ‚c‘ zum Beispiel, wählen:
9.
Rbc
(8)
E
Auch bei den folgenden Schritten muss man immer beachten, dass bei der Auswahl der
Konstanten für existenzquantifizierte Variablen immer neue Konstanten zu wählen sind, was
schließlich dazu führen wird, dass kein Widerspruch ableitbar ist:
9.
Rbc
(8)
E
10.
xRxc
(2)
U
11.
Rdc
(10)
E
(neue Konstante!)
12.
yRdy
(4)
U
(beliebige Konstante)
8
13.
yRdy
(12)
NU
14.
Rde
(13)
E
(neue Konstante)
(.)
(.)
Man kann an dieser Stelle schon erahnen, dass das Spiel ewig so weiter geht. Man kommt auf
keinen grünen Zweig – also auf keinen Widerspruch. Das Beispiel zeigt somit, dass man nicht
immer mit endlich vielen Schritten abschließen kann. Im 4. Beispiel lässt sich daher
(zunächst) keine Aussage darüber treffen, ob eine logische Wahrheit vorliegt oder nicht.
Wichtig ist noch das mehrfache Ausbeuten einer quantifizierten Zeile:
4. Trick:
All- und existenzquantifizierte Sätze können mehrfach nach (U) bzw. (E) weiterentwickelt
werden (mit verschiedenen Individuenkonstanten)!
Beobachtung: Der Zweig kann im vierten Beispiel nicht so weiterentwickelt werden, dass ein
Widerspruch entsteht.
Aber: Vielleicht ist die Angabe eines Gegenbeispiels möglich (Angabe einer
Interpretation, die den Satz falsch macht). Damit könnte man wenigstens
nachweisen, dass der Satz nicht logisch wahr ist.
Gegenbeispiel zu (4):
D = die natürlichen Zahlen
V(R) = x, y x ist größer als y
Es gibt zu jeder natürlichen Zahl eine natürliche Zahl, die größer ist als sie; aber es gibt keine
natürliche Zahl, die größer als alle natürliche Zahlen ist.
Damit ist gezeigt, dass (4) keine logische Wahrheit ist.
Wir fassen noch einmal zusammen, welche Aussage im Baumkalkül in welchem Fall
getroffen werden kann und wie wir bei der Entwicklung des Baumes vorgehen:
Satz: Baumkalkül für PL
Ein Satz von PL ist eine logische Wahrheit, wenn sich bei der Entwicklung seines Baumes
nach den dreizehn Regeln des Baumkalküls für PL in jedem Zweig ein Widerspruch ergibt.
9
Baumkalkül für PL:
Gegeben sei ein Satz aus PL.
1. Grundannahme (A): die Negation des Satzes ist wahr (1. Zeile).
2. Entwickle die 1. Zeile nach den 13 Regeln (die zweite und alle weiteren Zeilen, evtl.
unendlich viele).
3. Ergebnis: Der ursprüngliche Satz ist eine logische Wahrheit, wenn in jedem Zweig ein
Widerspruch auftritt (siehe Baumkalkül für AL).
Dabei gibt es noch einige „Tricks“, die beachtet werden sollten:
Tricks:
Es ist günstig, die folgenden Tricks zu beachten:
1.
Bei der Anwendung von (U) (‚Instanz wählen‘) solche Individuenkonstanten wählen,
die schon vorkamen!
2.
Negierte quantifizierte Formeln zuerst entwickeln!
3.
Existenzquantifizierte Formeln vor allquantifizierten Formeln entwickeln!
4.
All- und existenzquantifizierte Sätze können mehrfach nach (U) bzw. (E)
weiterentwickelt werden (mit verschiedenen Individuenkonstanten)!
Nicht vergessen: Bei der Anwendung von Regel (E) muss eine Individuenkonstante gewählt
werden, die in dem betreffenden Zweig bisher noch nicht vorkam!
Betrachten wir nun noch den Fall logischer Folgerungen. Nur wenn wir entscheiden können,
ob ein bestimmter Satz aus einer Menge anderer Sätze folgt, können wir entscheiden, ob ein
gültiges (prädikatenlogisches) Argument vorliegt. Und das war ja die Ausgangsfrage
gewesen.
Logische Folgerung in PL
Sind A1, ..., An-1 Sätze der Sprache PL, dann folgt der Satz An logisch aus den Sätzen A1, ...,
An-1, wenn jeder Zweig eines Wahrheitsbaumes, dessen Stamm aus den Sätzen A1, ..., An-1
und der Negation des Satzes An gebildet wird und der nur mit Hilfe der dreizehn Regeln des
Baumverfahrens der PL entwickelt wurde, mit einem ‚x‘ geschlossen werden kann (d.h. dass
in ihm ein Satz von PL sowohl in negierter als auch in nicht negierter Form vorkommt).
10
Betrachten wir nun einige Beispiele:
Beispiel 1: Ist der folgende Schluss gültig?
Alle F sind G, alle G sind H, also sind alle F H.
1.
x(FxGx)
A
2.
x(GxHx)
A
3.
x(FxHx)
A
4.
x(FxHx)
(3)
NU, negierte quantif. Sätze zuerst
5.
(FaHa)
(4)
E, existenzquantif. Sätze vor allq.
6.
Fa
(5)
NS
7.
Ha
(5)
NS
8.
FaGa
(1)
U
9.
Fa
10.
Ga
(8)
S
9x6
11.
GaHa
(2)
U
(11)
S
12. Ga
13. Ha
12x10
13x7
Ergebnis: Es handelt sich um einen gültigen Schluss!
11
Beispiel 2: Liegt eine logische Folgerung vor?
x(FxGx), x(FxHx) PL x(GxHx)
1.
x(FxGx)
A
2.
x(FxHx)
A
3.
x(GxHx)
A
4.
x(GxHx)
(3)
NE, neg. quantif. Sätze zuerst
5.
FaHa
(2)
E, existenzquantif. Formeln erst
6.
Fa
(5)
K
7.
Ha
(5)
K
8.
FaGa
(1)
U
9.
Fa
10. Ga
(8)
S
9x6
11. (GaHa)
(4)
U
(11)
NK
12.
Ga
12x10
13.
Ha
13x7
Ergebnis: Es liegt eine logische Folgerung vor!
12