Klausur-Musterl¨osungen Theoretische Physik IV - IAP TU

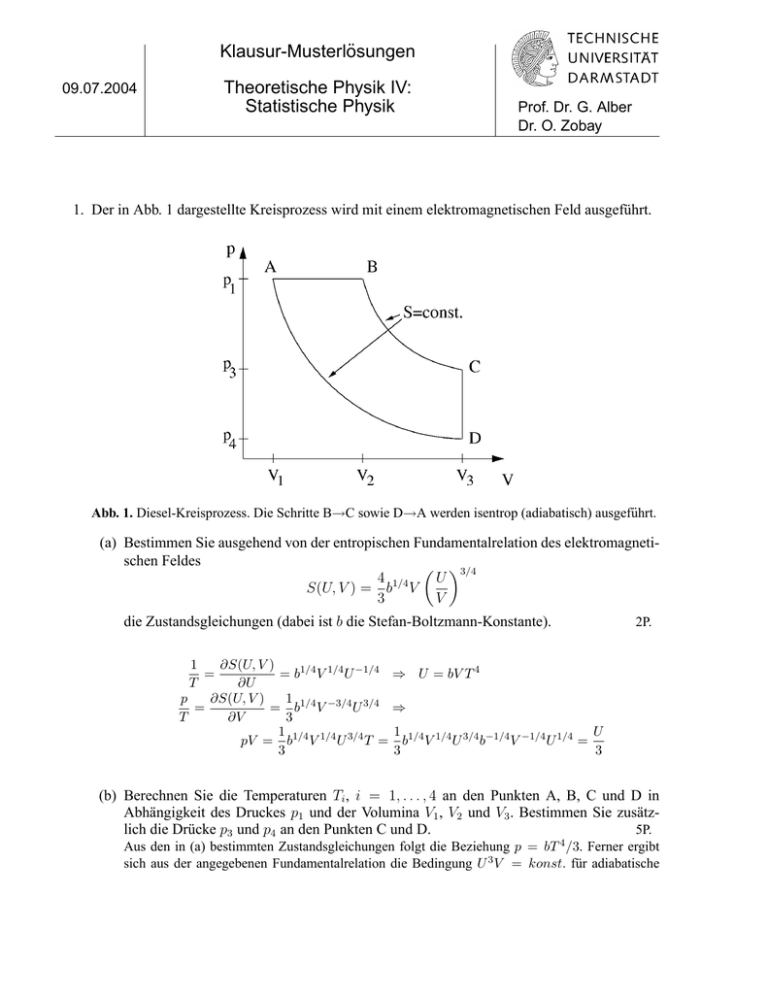
Klausur-Musterlösungen
09.07.2004
Theoretische Physik IV:
Statistische Physik
Prof. Dr. G. Alber
Dr. O. Zobay
1. Der in Abb. 1 dargestellte Kreisprozess wird mit einem elektromagnetischen Feld ausgeführt.
Abb. 1. Diesel-Kreisprozess. Die Schritte B→C sowie D→A werden isentrop (adiabatisch) ausgeführt.
(a) Bestimmen Sie ausgehend von der entropischen Fundamentalrelation des elektromagnetischen Feldes
3/4
4 1/4
U
S(U, V ) = b V
3
V
die Zustandsgleichungen (dabei ist b die Stefan-Boltzmann-Konstante).
2P.
1
∂S(U, V )
=
= b1/4 V 1/4 U −1/4 ⇒ U = bV T 4
T
∂U
p
∂S(U, V )
1
=
= b1/4 V −3/4 U 3/4 ⇒
T
∂V
3
1 1/4 1/4 3/4
1
U
pV = b V U T = b1/4 V 1/4 U 3/4 b−1/4 V −1/4 U 1/4 =
3
3
3
(b) Berechnen Sie die Temperaturen Ti , i = 1, . . . , 4 an den Punkten A, B, C und D in
Abhängigkeit des Druckes p1 und der Volumina V1 , V2 und V3 . Bestimmen Sie zusätzlich die Drücke p3 und p4 an den Punkten C und D.
5P.
Aus den in (a) bestimmten Zustandsgleichungen folgt die Beziehung p = bT 4 /3. Ferner ergibt
sich aus der angegebenen Fundamentalrelation die Bedingung U 3 V = konst. für adiabatische
Zustandsänderungen. Dies ist äquivalent zu pV 4/3 = konst. bzw. T 3 V = konst. Mit Hilfe dieser
Beziehungen ermittelt man für die Temperaturen
T1 = T2
T23 V2
T43 V3
=
T33 V3
=
T13 V1
=
3p1
b
1/4
,
⇒ T3 = T2
⇒ T4 = T1
V2
V3
1/3
V1
V3
1/3
=
=
3p1
b
1/4 3p1
b
1/4 V2
V3
1/3
V1
V3
1/3
,
.
Für die Drücke folgt
4/3
p1 V 2
4/3
p4 V 3
=
4/3
p3 V 3
=
4/3
p1 V 1
⇒ p3 = p 1
⇒ p4 = p 1
V2
V3
4/3
V1
V3
4/3
,
.
(c) Berechnen Sie die Arbeit, die jeweils in den Prozessschritten A→B, B→C, C→D und
D→A vom System verrichtet wird.
3P.
A→B:
∆WAB = p1 (V2 − V1 ) > 0,
"
B→C:
∆WBC = −∆UBC = 3P2 V2 − 3P3 V3 = 3P1 V2 1 −
C→D:
∆WCD = 0,
"
D→A:
∆WDA = −∆UBC = 3P4 V4 − 3P1 V1 = 3P1 V1
V1
V3
V2
V3
1/3 #
> 0,
#
1/3
− 1 < 0.
In den Schritten A→B und B→C gibt das System Arbeit nach außen ab, während im Schritt D→A
dem System Arbeit zugeführt wird.
(d) Ermitteln Sie die Wärmen, die in den vier Prozessschritten vom System aufgenommen
bzw. abgegeben werden.
2P.
A→B:
∆QAB = ∆WAB + ∆UAB = p1 (V2 − V1 ) + 3p1 (V2 − V1 ) = 4p1 (V2 − V1 ) > 0,
B→C:
∆QBC = 0,
C→D:
∆QCD = ∆UCD = 3p4 V3 − 3p3 V3 = 3
D→A:
p1 1/3
V3
4/3
V1
4/3
− V2
< 0,
∆QDA = 0.
Im Schritt A→B nimmt das System Wärme auf, während im Schritt C→D Wärme abgegeben
wird. In den adiabatischen Prozessschritten B→C und D→A wird Wärme weder zugeführt noch
abgegeben.
(e) Bestimmen Sie den Wirkungsgrad η dieses Kreisprozesses, und zeigen Sie, dass die Beziehung 0 < η < 1 erfüllt ist.
3P.
Der Wirkungsgrad für diesen Kreisprozess ist definiert als
P
∆Wi
η= Pi
.
∆Qauf
P
Dabei bezeichnet
i ∆Wi die Summe aller vom System aufgenommenen bzw. abgebenen ArP
beiten und ∆Qauf die insgesamt aufgenommene Wärme. Mit den Ergebnissen aus (c) und (d)
findet man
"
" #
1/3 #
X
V2
V1 1/3
∆Wi = p1 (V2 − V1 ) + 3p1 V2 1 −
+ 3p1 V1
−1
V3
V3
i
p1 4/3
4/3
= 4p1 (V2 − V1 ) + 3 1/3 V1 − V2
,
V3
X
∆Qauf = ∆QAB = 4p1 (V2 − V1 ).
Es ist also
η = 1−3
p1
1/3
V3
4/3
V2
4/3
− V1
3
=1−
4p1 (V2 − V1 )
4
V2
V3
1/3
1 − (V1 /V2 )4/3
.
1 − (V1 /V2 )
Da V1 < V2 und V2 < V3 , folgt aus dieser Darstellung die Beziehung 0 < η < 1. Dies ergibt
sich aus der Tatsache, dass die Funktion y = (1 − x4/3 )/(1 − x) (x entspricht hier V1 /V2 ) für
0 ≤ x ≤ 1 nur Werte 1 ≤ y ≤ 4/3 annimmt. Zusammen mit dem Vorfaktor 3/4 wird also von der
1 immer nur etwas abgezogen, das kleiner als 1 (aber größer als 0) ist.
2. Gegeben sei ein ideales Gas von strukturlosen Spin- 21 Teilchen in einer dreidimensionalen isotropen harmonischen Teilchenfalle mit Frequenz ω.
(a) Wie lauten die Einteilchenenergien und der Hamiltonoperator dieses Systems in zweiter
Quantisierung? Wievielfach sind die Einteilchenenergien entartet?
2P.
Der Hamiltonoperator dieses Systems lautet
b =
H
∞
X
X
εn1 n2 n3 ,σ b
a†n1 n2 n3 ,σ b
an1 n2 n3 ,σ
n1 ,n2 ,n3 =0 σ=±
mit den Einteilchen-Energien
εn1 n2 n3 ,σ = ~ω n1 + n2 + n3 +
3
2
.
Der Index σ = ± charakterisiert den Spin-Freiheitsgrad. Die Entartung der Einteilchenenergie
εn = ~ω(n + 32 ) beträgt
(n + 1)(n + 2)
g(n) = 2
2
(vgl. Aufgabe 3, Blatt 11; der zusätzliche Faktor 2 ist auf den Spin-Freiheitsgrad zurückzuführen).
Der Operator b
an1 n2 n3 ,σ erfüllt die Antikommutator-Beziehungen
h
i
b
an1 n2 n3 ,σ , b
a†m1 m2 m3 ,σ0
= δn1 ,m1 δn2 ,m2 δn3 ,m3 δσ,σ0 ,
+
h
i
b
an1 n2 n3 ,σ , b
am1 m2 m3 ,σ0 + = b
a†n1 n2 n3 ,σ , b
a†m1 m2 m3 ,σ0
= 0.
+
(b) Zeigen Sie, dass die großkanonische Zustandssumme im Kontinuumlimes, der durch N →
∞, ω → 0, N ω 3 = konst., kB T ~ω charakterisiert ist, die Gestalt
Z ∞
1
x3
ln ZG (λ1 , λ2 ) =
dx
3(~ωλ1 )3 0
exp(x + λ2 ) + 1
besitzt.
3P.
Es gilt
∞
X
ln ZG (λ1 , λ2 ) =
X
ln [1 + exp (−λ1 εn1 n2 n3 ,σ − λ2 )]
n1 ,n2 ,n3 =0 σ=±
∞
X
= 2
n=0
(n + 1)(n + 2)
ln [1 + exp (−λ1 ~ω(n + 3/2) − λ2 )] .
2
Im Kontinuumlimes λ1 ~ω → 0 erhält man daraus mit x = ~ωλ1 n und partieller Integration
Z ∞
ln ZG (λ1 , λ2 ) ≈
dn n2 ln[1 + exp(−λ1 ~ωn − λ2 )]
0
Z ∞
1
dx x2 ln[1 + exp(−x − λ2 )]
=
(~ωλ1 )3 0
Z ∞
1
x3
=
dx
.
3(~ωλ1 )3 0
exp(x + λ2 ) + 1
(1)
Dabei wurde beim Übergang von der zweiten zur dritten Zeile partiell integriert.
(c) Vereinfachen Sie die allgemeine Zustandssumme aus (b) für den Fall eines klassischen
idealen Gases und bestimmen Sie daraus die mittlere Teilchenzahl N (T, µ) und die innere Energie U (T, N ). Welche Bedingung müssen die Teilchenzahl und die Temperatur
erfüllen, damit die Näherung eines klassischen idealen Gases anwendbar ist?
5P.
Der Grenzfall des klassischen idealen Gases ist durch exp λ2 1 charakterisiert. Der Integrand
in (??) kann dann durch x3 exp(−x − λ2 ) genähert werden, und man erhält
1
ln ZG (λ1 , λ2 ) =
3
kB T
~ω
3
Z
exp(−λ2 )
∞
3
dx x exp(−x) = 2
0
kB T
~ω
3
exp(−λ2 ).
Damit ergibt sich mit −λ2 = µ/kB T
∂ ln ZG
kB T 3
N (T, µ) = −
= ln ZG = 2
exp(µ/kB T ),
∂λ2
~ω
∂ ln ZG
3
U = −
=
ln ZG = 3kB T N.
∂λ1
λ1
Das Resultat für U steht im Einklang mit dem klassischen Gleichverteilungssatz, nach dem jeder
Freiheitsgrad, der quadratisch in die Hamiltonfunktion eingeht, einen Beitrag kB T /2 zur inneren
Energie liefert. Im Fall des harmonischen Oszillators gehen alle 3N Orts- und Impulskoordinaten
quadratisch ein.
Die Bedingung exp λ2 1 führt auf die Beziehung kB T 2−1/3 ~ωN 1/3 , die im klassischen
Grenzfall erfüllt sein muss.
(d) Betrachten Sie den entarteten Fall des nicht wechselwirkenden Spin- 12 Systems. Vereinfachen Sie die allgemeine Zustandssumme aus (b) im Grenzfall extremer Entartung, d.h.,
T → 0. Bestimmen Sie die mittlere Teilchenzahl N (T, µ), das chemische Potenzial
µ(T, N ) und die innere Energie U (T, N ) in diesem Grenzfall.
5P.
Im Grenzfall extremer Entartung gilt exp λ2 1, d.h., −λ2 1. Die Funktion (exp(x + λ2 ) +
1)−1 hat dann die Gestalt eines Fermi-Blocks“, d.h., sie wechselt für wachsendes x in der Nähe
”
von x = −λ2 sehr rasch von 1 auf 0. Daher ergibt sich näherungsweise für die Zustandssumme
Z
1 kB T 3 −λ2
1 kB T 3
3
ln ZG (λ1 , λ2 ) ≈
dx x =
(−λ2 )4 .
3 ~ω
12 ~ω
0
Damit erhält man
1
∂ ln ZG
=
N (T, µ) = −
∂λ2
3
kB T
~ω
3
1
(−λ2 ) =
3
3
kB T
~ω
3 µ
kB T
3
=
1 µ 3
,
3 ~ω
d.h.,
~ω
,
kB T
µ(T, N ) = −kB T λ2 = (3N )1/3 ~ω,
−λ2 = (3N )1/3
U
∂ ln ZG
3
1
= −
=
ln ZG = 3kB T
∂λ1
λ1
12
kB T
~ω
3
1
(−λ2 )4 = (3N )4/3 ~ω.
4
3. Gegeben sei ein ideales Gas von Bosonen mit Spin J im ultrarelativistischen Grenzfall vernachlässigbarer Ruhemasse, das in einem Behälter mit Volumen V eingeschlossen ist. Betrachten Sie im Folgenden den thermodynamischen Limes dieses Systems.
(a) Zeigen Sie, dass die großkanonische Zustandssumme oberhalb der kritischen Temperatur
Tc für Bose-Einstein-Kondensation durch
ln ZG (λ1 , λ2 ) = (2J + 1)
gegeben ist.
8πV
g4 (e−λ2 )
(2π~λ1 c)3
3P.
Im ultrarelativistischen Grenzfall sind die Einteilchenenergien durch ε(~
p) = c|~
p| gegeben (vgl.
Blatt 9). Im Kontinuumlimes gilt dann für die großkanonische Zustandssumme oberhalb der kritischen Temperatur
Z
V
3
−λ1 c|~
p|−λ2
d
p
ln
1
−
e
ln ZG (λ1 , λ2 ) = −(2J + 1)
(2π~)3
Z ∞
4πV
2
−λ1 cp−λ2
= −(2J + 1)
dpp
ln
1
−
e
(2π~)3 0
Z ∞
4πV
2
−x−λ2
= −(2J + 1)
dxx
ln
1
−
e
(2π~λ1 c)3 0
Z ∞
4πV
x3
= (2J + 1)
dx
3(2π~λ1 c)3 0
ex+λ2 − 1
4πV
8πV
= (2J + 1)
Γ(4)g4 (e−λ2 ) = (2J + 1)
g4 (e−λ2 ).
3(2π~λ1 c)3
(2π~λ1 c)3
Dabei wurde beim Übergang von der dritten zur vierten Zeile partiell integriert und in der nächsten
Umformung eine der Beziehungen verwendet, die in der Formelsammlung für die Bose-EinsteinFunktion angegeben ist.
(b) Ermitteln Sie mit Hilfe der großkanonischen Zustandssumme die innere Energie U , den
Druck p, die Teilchenzahl N sowie die Entropie als Funktion von T , V und µ.
6P.
U
p =
N
3
3V (kB T )4
∂ ln ZG
=
ln ZG = (2J + 1) 2
g4 (eµ/kB T ),
∂λ1
λ1
π (~c)3
kB T
(kB T )4
g4 (eµ/kB T ),
ln ZG = (2J + 1) 2
V
π (~c)3
∂ ln ZG
V (kB T )3
−
= (2J + 1) 2
g3 (eµ/kB T ),
∂λ2
π (~c)3
1
µ
1
(U + pV − µN ) = (3kB T ln ZG + kB T ln ZG − µN ) = 4kB ln ZG − N
T
T
T
2
4V (kB T )3
µV
(k
T
)
B
(2J + 1)kB 2
g4 (eµ/kB T ) − (2J + 1)kB 2
g3 (eµ/kB T )
π (~c)3
π (~c)3
i
V (kB T )2 h
µ/kB T
µ/kB T
(2J + 1)kB 2
4k
T
g
(e
)
−
µg
(e
)
.
4
3
B
π (~c)3
= −
=
S =
=
=
(c) Bestimmen Sie Tc in Abhängigkeit von der Teilchendichte.
3P.
Aus Aufgabenteil (b) folgt, dass die Teilchendichte n in Abhängigkeit von der Temperatur T und
dem chemischen Potential µ durch
n = (2J + 1)
(kB T )3
g3 (eµ/kB T )
π 2 (~c)3
gegeben ist. Die Funktion g3 (x) ist nur für 0 ≤ x ≤ 1 definiert und nimmt ihr Maximum g3 (1) =
ζ(3) bei x = 1 an. Die maximale Teilchendichte, die bei festem T erreicht werden kann, ohne dass
Kondensation eintritt, ergibt sich also für µ = 0 und hat den Wert
n = (2J + 1)
(kB T )3
ζ(3).
π 2 (~c)3
Anders ausgedrückt, beträgt die kritische Temperatur Tc für Bose-Einstein-Kondensation bei gegebener Teilchendichte
1/3
π2n
kB Tc = ~c
.
(2J + 1)ζ(3)
(d) Wie hängt die relative Anzahl N0 /N der Teilchen im Kondensat von der skalierten Temperatur T /Tc ab?
3P.
Unterhalb der Kondensationstemperatur müssen bei der Berechnung der Teilchenzahl die Teilchen
im Kondensat separat betrachtet werden. Da µ = 0, folgt mit den Ergebnissen aus (b) und (c)
N
= N0 + (2J + 1)
= N0 + N
T
Tc
V (kB T )3
V (kB T )3
(kB Tc )3
ζ(3)
=
N
+
(2J
+
1)
ζ(3)
·
0
π 2 (~c)3
π 2 (~c)3
(kB Tc )3
3
.
Es ist also
N0
=1−
N
T
Tc
3
.
Formelsammlung
• Bose-Einstein-Funktionen
−λ2
gα (e
1
) =
Γ(α)
Z
∞
0
xα−1
dx x+λ2
e
−1
∂
gα (e−λ2 ) = −gα−1 (e−λ2 )
∂λ
• Gamma-Funktion
Z
∞
Γ(n + 1) =
dxxn e−x = n!
(n ∈ N)
0
• Fermi-Dirac-Funktionen
−λ2
fα (e
Z
) =
∞
dx
0
xα−1
ex+λ2 + 1