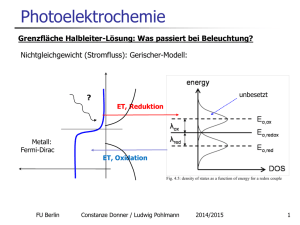
Doppelschicht (Folien)

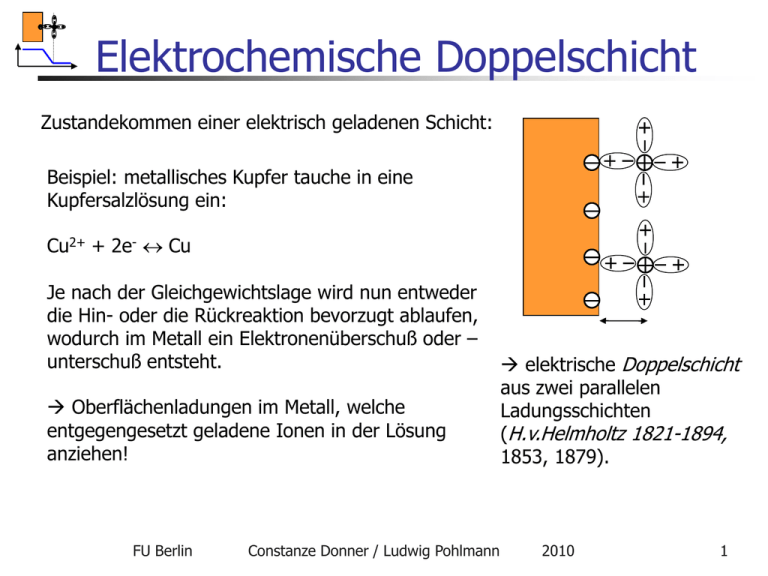
Elektrochemische Doppelschicht
Zustandekommen einer elektrisch geladenen Schicht:
Beispiel: metallisches Kupfer tauche in eine
Kupfersalzlösung ein:
Cu2+ + 2e-  Cu
Je nach der Gleichgewichtslage wird nun entweder
die Hin- oder die Rückreaktion bevorzugt ablaufen,
wodurch im Metall ein Elektronenüberschuß oder –
unterschuß entsteht.
 Oberflächenladungen im Metall, welche
entgegengesetzt geladene Ionen in der Lösung
anziehen!
FU Berlin
Constanze Donner / Ludwig Pohlmann
 elektrische Doppelschicht
aus zwei parallelen
Ladungsschichten
(H.v.Helmholtz 1821-1894,
1853, 1879).
2010
1
Plattenkondensator-Modell


starre Doppelschicht von
solvatisierten Ionen und
Elektronen auf der Metallseite
„Plattenabstand“: einige
Moleküldurchmesser

Ladungsfreier Raum zwischen den
Schichten: Linearer Potentialabfall
d 2



mit   0
2
dx
 r 0
Metall
FU Berlin
äußere HH-Schicht
Constanze Donner / Ludwig Pohlmann
2010
2
Helmholtz
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
3
Konsequenzen I
„Plattenkondensator“ mit kleinstmöglichem Plattenabstand!


Extrem hohe Feldstärke:
 = 500 mV, d = 0.5 nm
 Feldstärke E = 109 V/m !
Zum Vergleich:
Durchschlagsfeldstärke:
Luft: 106, Quarz: 108 V/m
Diese enormen Feldstärken sind
notwendig (und hinreichend), um
chemische Bindungen brechen
bzw. neu formen zu können!
Elektrochemische Reaktionen können nur in der
Helmholtzschicht stattfinden! EC ist Surface Science!
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
4
Konsequenzen II
„Plattenkondensator“ mit kleinstmöglichem Plattenabstand!

Riesige Kapazität:

Kapazität pro Fläche beim Plattenkondensator: C  r 0
d


Wasser: r = 78,5  C = 350 F/cm2
in Wirklichkeit kleiner, ca. 10-50 F/cm2, da r in
der starren Doppelschicht kleiner ist
 Anwendung für Kondensatoren!
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
5
Doppelschichtkondensatoren


Kapazität: 10-40 F/cm2
Seit 1971 (1957 Patent)
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
6
Superkondensatoren

Prinzip: poröse
Kohlenstoffelektroden mit einer
sehr großen inneren Oberfläche!
(Aktivkohle, Aerogele)
 Kapazitäten bis zu 100 F / g !
1
W  CU 2
2

Energiedichte: 4 Wh / kg  bis zu 60 Wh / kg

Forschung: neue Elektrodenmaterialien, geeignetere Elektrolyte
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
7
Anwendungsperspektiven
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
8
Gouy-Chapman-Modell



Grundidee: zwei gegenläufig Prozesse
Das elektrostatische Feld der Elektrode zieht
entgegengesetzt geladene Ionen an
Die Molekularbewegung zerstört immer wieder
jede Ordnung
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
9
Gouy-Chapman II


Analogie?

Vergleichbar mit der barometrischen Höhenformel?
  0e
Allerdings:



h
hs
Das Gravitationspotential ist
annähernd linear und unabhängig
von der Luftdichte
Das elektrische Potential hängt von
der Ladungsdichte selbst ab:
d 2x 
x 

2
dx
 r 0
FU Berlin
und
 Wohl doch
komplizierter!?
 z ex  
x    z i en i0  exp   i

i
kT 

Constanze Donner / Ludwig Pohlmann
2010
10
Gouy-Chapman III

Trotz aller Kompliziertheit: näherungsweise ist die
Lösung der Gleichungen rein exponentiell:
1
2 N Ae2 I
 x
x   0  exp    mit der Debye-Länge:





 r 0 kT
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
11
Nullladungspotential

Näherungsweise gilt für die Ladung in der Doppelschicht:

 r  00
   M    x dx  

0
Folgerungen:

Potentialdifferenz = 0  Überschußladung = 0

Schichtdicke „Plattenkondensator“: Debye-Länge!

Minimum der differentiellen Kapazität im Nulladungspotential:
d
2z 2 e 2  r  0 n 0
 ze 0 
C

cosh

d0
kT
2
kT


FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
12
Exkurs: Adsorption von Zusätzen
Das Nullladungspotential steuert die potentialabhängige Adsorption von
polaren und unpolaren Molekülen, welche selbst an der Reaktion nicht
teilnehmen (Additive):

Konzentration
Polare Moleküle,
positive Seite
negativ

Polare Moleküle,
negative Seite
unpolare Moleküle
PZC
positiv
Das Nullladungspotential hat nichts mit dem Nernst-Potential zu
tun, welches das elektrochemisch Gleichgewicht definiert!
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
13
Synthese: Stern-Modell


Das GC-Modell ist geeignet für die Nähe des Nullladungspotentials,
das HH-Modell für größere Entfernungen davon
HH-Schicht und die diffuse GC-Schicht sind geometrisch
hintereinander angeordnet
Logisch ist eine Synthese: Reihenschaltung beider Kondensatoren
 Modell von Stern 1888-1969 (1924):
1
1
1
 H  GC
Cd Cd Cd 0 
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
14
Stern-Modell
Potential
Entfernung von d. Grenzfläche
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
15
Stern-Modell
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
16
Kapazitätsverlauf
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
17
Reale Doppelschicht
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
18
Portraits
FU Berlin
Constanze Donner / Ludwig Pohlmann
2010
19