Theorie: Die Kepler`sche Fassregel

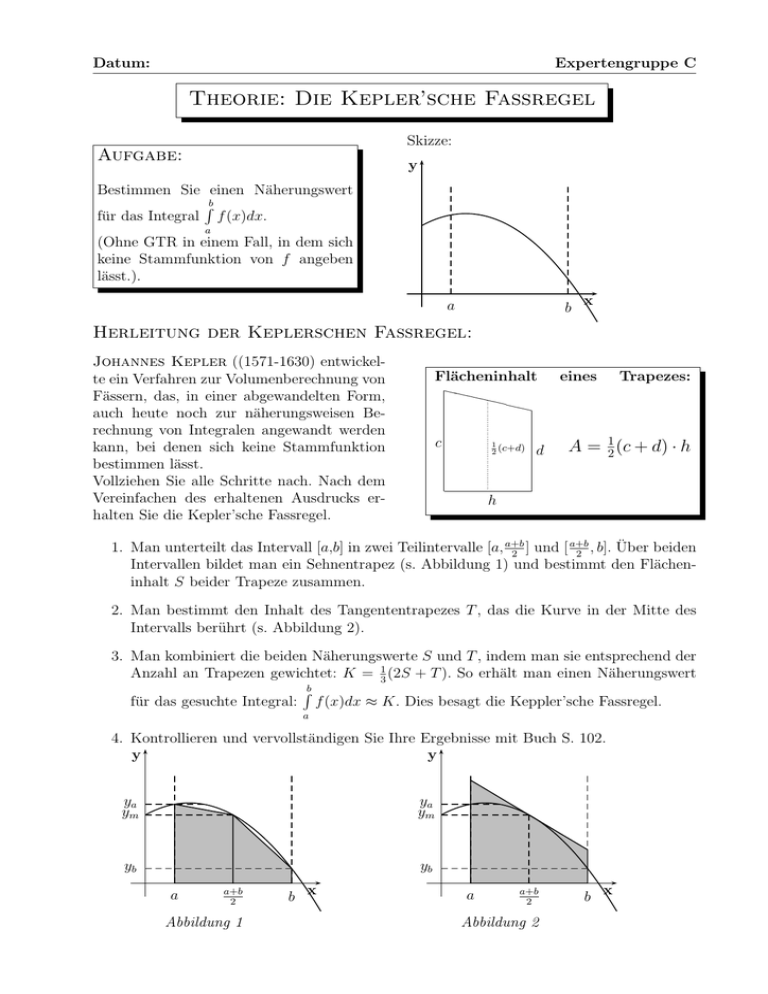
Datum:
Expertengruppe C
Theorie: Die Kepler’sche Fassregel
Skizze:
Aufgabe:
y
Bestimmen Sie einen Näherungswert
Rb
für das Integral f (x)dx.
a
(Ohne GTR in einem Fall, in dem sich
keine Stammfunktion von f angeben
lässt.).
a
b
x
Herleitung der Keplerschen Fassregel:
Johannes Kepler ((1571-1630) entwickelte ein Verfahren zur Volumenberechnung von
Fässern, das, in einer abgewandelten Form,
auch heute noch zur näherungsweisen Berechnung von Integralen angewandt werden
kann, bei denen sich keine Stammfunktion
bestimmen lässt.
Vollziehen Sie alle Schritte nach. Nach dem
Vereinfachen des erhaltenen Ausdrucks erhalten Sie die Kepler’sche Fassregel.
Flächeninhalt
XXX
X
c
XX
eines
Trapezes:
X
1
(c+d)
2
d
A = 12 (c + d) · h
h
1. Man unterteilt das Intervall [a,b] in zwei Teilintervalle [a, a+b
] und [ a+b
, b]. Über beiden
2
2
Intervallen bildet man ein Sehnentrapez (s. Abbildung 1) und bestimmt den Flächeninhalt S beider Trapeze zusammen.
2. Man bestimmt den Inhalt des Tangententrapezes T , das die Kurve in der Mitte des
Intervalls berührt (s. Abbildung 2).
3. Man kombiniert die beiden Näherungswerte S und T , indem man sie entsprechend der
Anzahl an Trapezen gewichtet: K = 31 (2S + T ). So erhält man einen Näherungswert
Rb
für das gesuchte Integral: f (x)dx ≈ K. Dies besagt die Keppler’sche Fassregel.
a
4. Kontrollieren und vervollständigen Sie Ihre Ergebnisse mit Buch S. 102.
y
y
ya
ym
ya
ym
yb
yb
a
a+b
2
Abbildung 1
b
x
a
a+b
2
Abbildung 2
b
x
Datum:
Expertengruppe C
Theorie: Mittelwerte von Funktionen
Skizze:
y
Aufgabe:
f
Bestimmen Sie den Mittelwert m der
Funktionswerte von f auf dem Intervall
[a,b].
m
a
b
x
Herleitung einer allgemeinen Formel:
1. Wie Sie den Mittelwert einer Reihe von Zahlen berechnen, ist Ihnen bekannt: Man
summiert sie und teilt durch ihre Anzahl. Was ist der Mittelwert der Zahlen 12, 14,
11, 8, 15 und 12? Die erhaltene Zahl heißt das arithmetische Mittel der Zahlen.
2. Das Problem bei der Bestimmung des Mittelwertes von Funktionswerten ist, dass auf
dem Intervall [a,b] beliebig viele Funktionswerte liegen. Man kann nicht durch ihre
Anzahl teilen, weil diese unendlich groß ist. Deswegen betrachten wir die Bedeutung
des Mittelwertes genauer.
Damit m Mittelwert der Funktionswerte von f ist, muss die Gerade mit der Gleichung
y = m mit dem Graphen der Funktion zwei gleich große Flächen begrenzen (s. Skizze). Nur so können entsprechend viele Werte oberhalb wie unterhalb des Mittelwertes
liegen. Schraffieren Sie die Flächen in der Skizze oben.
3. Die Geraden mit den Gleichungen y = m, x = a, x = b und die x-Achse begrenzen ein
Rechteck. Wie groß ist dessen Inhalt?
4. Vergleichen wir dieses Rechteck mit dem Flächeninhalt zwischen dem Graphen von f
und der x-Achse, so erkennen wir einen einfachen Zusammenhang. Welchen? Formulieren Sie diesen Zusammenhang in Form einer Formel, in der sie den Flächeninhalt
unter dem Graphen von f mit einem geeigneten Integral ausdrücken.
5. Lösen Sie die erhaltene Formel nach m auf und formulieren sie das Ergebnis als Merksatz.
6. Kontrollieren Sie Ihren Merksatz mit der Definition im Buch S. 100.