TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienkurs Analysis 1

TECHNISCHE UNIVERSITÄT MÜNCHEN
Ferienkurs Analysis 1
WS 08/09
Lösung 1. Übungsblatt
Elisabeth Brunner
Hannah Jörg
Lösung 2.1.
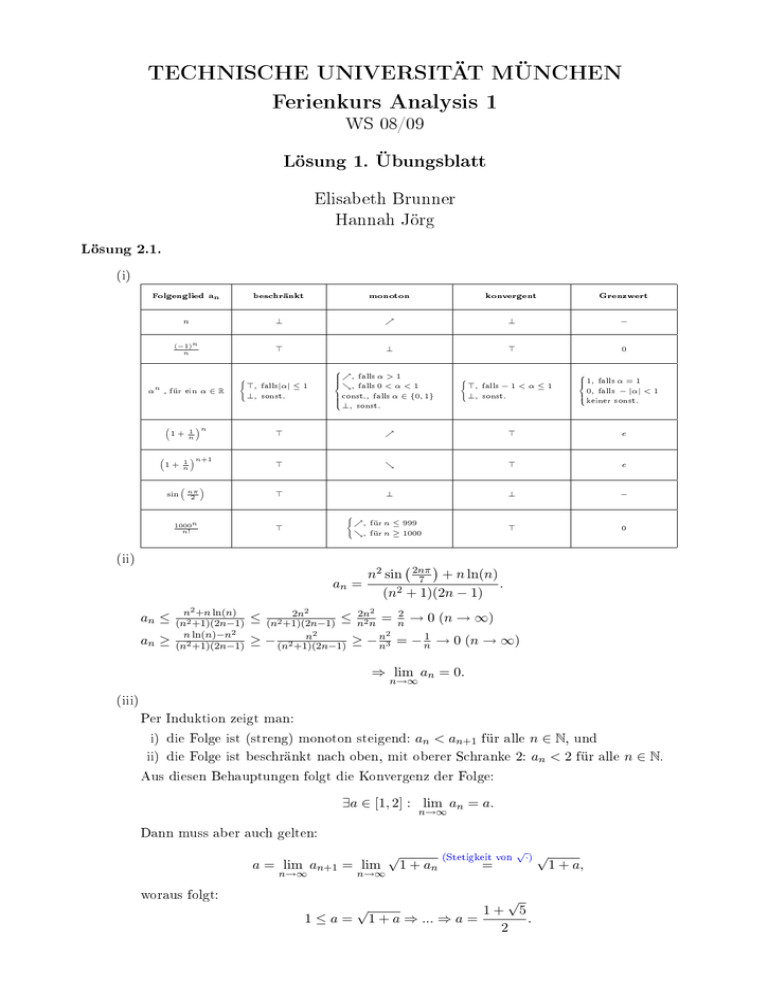
(i)
Folgenglied an
beschränkt
monoton
konvergent
Grenzwert
n
⊥
%
⊥
−
(−1)n
n
>
⊥
>
0
(
α
n
, für ein
α∈R
>,
⊥,
falls|α|
≤1
sonst.

%, falls α > 1




&, falls 0 < α < 1

const., falls α ∈ {0, 1}



⊥, sonst.
(
>,
⊥,
−1<α≤1
sonst.
falls


1, falls α = 1
0, falls − |α| < 1

keiner sonst.
1 n
1+ n
>
%
>
e
1 n+1
1+ n
>
&
>
e
>
⊥
⊥
−
n ≤ 999
n ≥ 1000
>
0
sin
nπ
2
(
1000n
n!
>
(ii)
%,
&,
für
für
n2 sin 2nπ
+ n ln(n)
7
an =
.
2
(n + 1)(2n − 1)
an ≤
an ≥
n2 +n ln(n)
(n2 +1)(2n−1)
n ln(n)−n2
(n2 +1)(2n−1)
≤
≥
2
2n2
≤ n2n2 n = n2 → 0 (n → ∞)
(n2 +1)(2n−1)
2
n2
− (n2 +1)(2n−1)
≥ − nn3 = − n1 → 0 (n →
∞)
⇒ lim an = 0.
n→∞
(iii)
Per Induktion zeigt man:
i) die Folge ist (streng) monoton steigend: an < an+1 für alle n ∈ N, und
ii) die Folge ist beschränkt nach oben, mit oberer Schranke 2: an < 2 für alle n ∈ N.
Aus diesen Behauptungen folgt die Konvergenz der Folge:
∃a ∈ [1, 2] : lim an = a.
n→∞
Dann muss aber auch gelten:
a = lim an+1
n→∞
√
= lim 1 + an
woraus folgt:
1≤a=
n→∞
√
(Stetigkeit von
=
√
·)
√
1+ 5
1 + a ⇒ ... ⇒ a =
.
2
√
1 + a,
Lösung 2.2.
an = sin
nπ :
6
√
diese Folge hat sieben Häufungspunkte: 0, ± 21, ± 23 , ±1.
Z.B. für nk = 12k + 1 gilt ank = sin 2kπ + π6 = 12 .
n
bn = (−1) sin
Es gilt:
n2 + n ln(n)
π
(n + 1)(2n − 3)
(es wird benutzt: lim
x→∞
ln(x)
= 0)
x
n2 + n ln(n)
1
= .
n→∞ (n + 1)(2n − 3)
2
π Daraus ergeben sich die Häufungspunkte der Folge: ± sin
= ±1,
2
und die konvergenten Teilfolgen: (a2n−1 )n∈N → −1 und (a2n )n∈N → 1.
1 n
n2
1+
:
cn = (−1)
4n
Mit:
1
1 n
lim 1 +
= e 4 , und
n→∞
4n
(
1, falls n grade,
2
(−1)n = (−1)n =
−1, sonst
lim
1
ergeben sich die Häufungspunkte der Folge: ±e 4
und ihre konvergenten Teilfolgen:
1
(a2n−1 )n∈N → −e 4
1
und (a2n )n∈N → e 4 .
3
:
dn = (−1)
2+
n
Häufungspunkte: ±2, konvergente Teilfolgen: (a2n−1 )n∈N → 2, (a2n )n∈N → −2
(n−1)
Lösung 2.3.
an =
cos(1!)
1·2
+
cos(2!
2·3
+ ... +
| an+p − an | =
≤
=
=
<
cos(n!)
n(n+1)
ist eine Cauchy-Folge, also konvergent:
cos((n + 1)!)
cos((n
+
2)!
cos((n
+
p)!)
(n + 1)(n + 2) + (n + 2)(n + 3) + ... + (n + p)(n + (p + 1)) 1
1
1
+
+ ... +
(n + 1)(n + 2) (n + 2)(n + 3)
(n + p)(n + (p + 1))
1
1
1
1
1
−
+
− ... +
−
n+1 n+2 n+2
n+p n+p+1
1
1
−
n+1 n+p+1
1
→ 0 (n → ∞).
n
Lösung 2.4.
Die Abbildung
(
N2 → N,
f:
(p, q) 7→ (p+q−2)(p+q−1)
+p
2
ist eine Bijektion, und besitzt die Umkehrfunktion g : N → N2 . Die Abbildung
(
N2 → Q+ ,
h:
(p, q) 7→ pq
ist eine Surjektion. Also ist die Abbildung:
a = h ◦ g, N → Q+
ebenfalls eine Surjektion.
Die mittels:


0, falls n = 1,
αn = a(k) falls n = 2k, k ∈ N,


−a(k) falls n = 2k − 1, k ∈ N
denierte Folge (αn )n∈N ist damit eine Aufzählung aller rationalen Zahlen. Die Häufungspunkte
dieser Folge sind alle reellen Zahlen!
Lösung 2.5.
a) Für n ≥ 2 gilt: xn+1 − xn =
. . . = (x2 − x1 ) · (− 12 )n−1
xn +xn−1
2
− xn = (xn − xn−1) · (− 21 ) = (xn−1 − xn−2 ) · (− 12 )2 =
= (b − a) · (− 12 )n−1 .
b) Aus der Darstellung:
xn = (xn − xn−1 ) + (xn−1 − xn−2 ) + (xn−2 − xn−3 ) + . . . + (x2 − x1 ) + x1
für n ≥ 2 folgt:
P
1 k
xn = (b−a)·(− 21 )n−2 +(b−a)·(− 12 )n−3 +. . .+(b−a)·(− 21 )0 +a = a+(b−a) n−2
k=0 (− 2 ) =
1−(− 12 )n−2
→
1+ 12
a+2b
limn→∞ xn = 3
a + (b − a)
Also
a + 23 (b − a) =
a+2b
3
(n → ∞)