Trigonometrische Funktionswerte für besondere Winkel Satz 1.: In

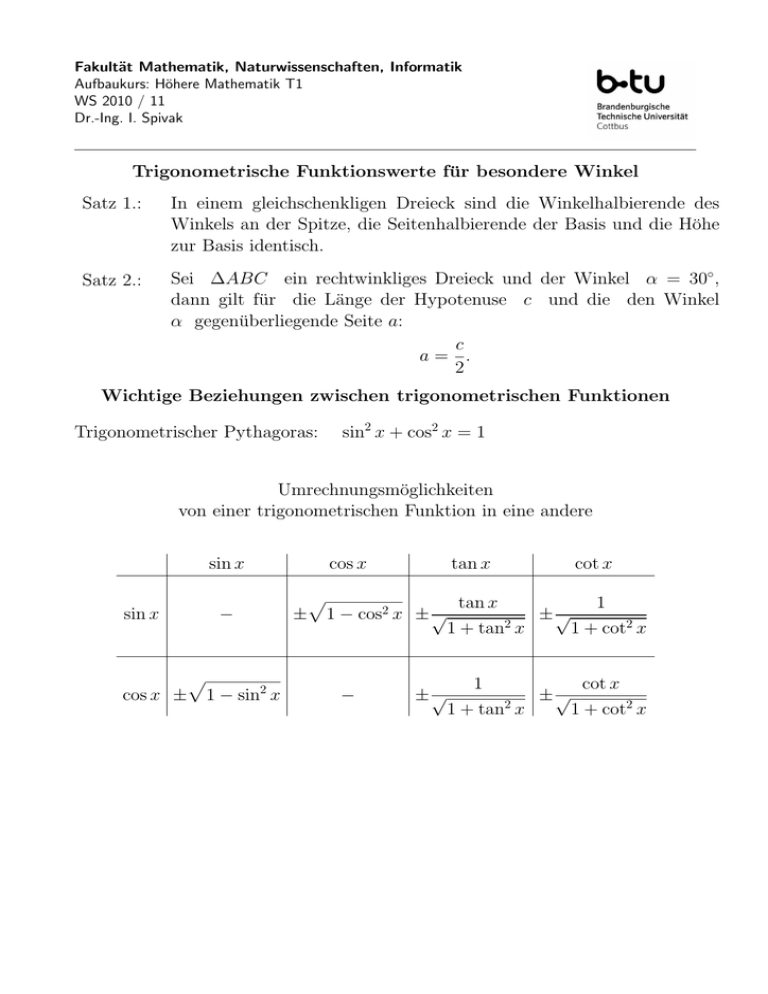
Fakultät Mathematik, Naturwissenschaften, Informatik
Aufbaukurs: Höhere Mathematik T1
WS 2010 / 11
Dr.-Ing. I. Spivak
Trigonometrische Funktionswerte für besondere Winkel
Satz 1.:
In einem gleichschenkligen Dreieck sind die Winkelhalbierende des
Winkels an der Spitze, die Seitenhalbierende der Basis und die Höhe
zur Basis identisch.
Satz 2.:
Sei ∆ABC ein rechtwinkliges Dreieck und der Winkel α = 30◦ ,
dann gilt für die Länge der Hypotenuse c und die den Winkel
α gegenüberliegende Seite a:
c
a= .
2
Wichtige Beziehungen zwischen trigonometrischen Funktionen
Trigonometrischer Pythagoras:
sin2 x + cos2 x = 1
Umrechnungsmöglichkeiten
von einer trigonometrischen Funktion in eine andere
sin x
sin x
−
p
cos x ± 1 − sin2 x
cos x
tan x
cot x
p
tan x
1
√
± 1 − cos2 x ± √
±
1 + tan2 x
1 + cot2 x
−
±√
1
1 + tan2 x
±√
cot x
1 + cot2 x
Additionstheoreme
sin (x1 ± x2 ) = sin x1 cos x2 ± cos x1 sin x2
cos (x1 ± x2 ) = cos x1 cos x2 ∓ sin x1 sin x2
cos 2x = cos2 x − sin2 x
r
1 + cos 2x
|cos x| =
2
sin 2x = 2 sin x cos x,
r
1 − cos 2x
|sin x| =
,
2
tan (x1 ± x2 ) =
tan x1 ± tan x2
1 ∓ tan x1 tan x2
x+y
x−y
cos
2
2
x+y
x−y
cos
sin x − sin y = 2 sin
2
2
x−y
x+y
cos
cos x + cos y = 2 cos
2
2
x−y
x+y
sin
cos x − cos y = −2 sin
2
2
sin x + sin y = 2 sin
2
Beziehungen zwischen den trigonometrischen Funktionen unterschiedlicher
Winkel
x
π−α
π+α
sin x
sin α
− sin α − sin α − sin α
cos x − cos α − cos α
2 π−α
cos α
−α
cos α
tan x − tan α
tan α
− tan α − tan α
cot x − cot α
cot α
− cot α − cot α
x
π
2
−α
sin x cos α
cos x sin α
π
2
+α
cos α
3π
2
−α
3π
2
+α
− cos α − cos α
− sin α − sin α
sin α
tan x cot α − cot α
cot α
− cot α
cot x tan α − tan α
tan α
− tan α
3