Funktionsweise

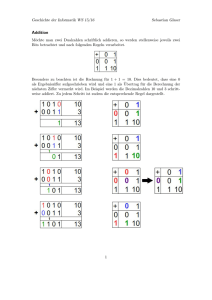
Der chinesische Abakus –
„suan pan“
Die nachfolgende Präsentation gibt einen Einblick in die
Grundrechenarten am „suan pan“ (chinesischer Abakus).
Sie dient lediglich als Ergänzung zur meinem Projektvortrag und ist
vor allem für ein Selbststudium gedacht!!!
Vorab jedoch noch eine kleine Bemerkung:
„Ein Bild sagt mehr als 1000 Worte.“
Die Beschreibungen der einzelnen Rechenvorgänge
hören sich zuerst sehr unverständlich an. Zum besseren
Verständnis habe ich nach jedem Gedankengang ein Bild
eingefügt, auf dem die Schritte direkt zu erkennen sind!
Viel Spaß…
Allgemeine Funktionsweise:
•
•
•
•
•
•
•
•
Der Abakus beschreibt ein allgemeines Stellenwertsystem
Jeder Stab repräsentiert eine Dezimalstelle: ganz rechts die Einerstelle, der
Zweite Stab von rechts die Zehnerstelle usw.
Jede Perle im unteren Teil steht für eine Einheit der jeweiligen Dezimalstelle
Jede Perle im oberen Teil steht für fünf Einheiten der jeweiligen
Dezimalstelle
Eine Perle wird gezählt, wenn sie in Richtung der Querstange geschoben
wird (die 0 wird also dargestellt, indem keine Kugel, an der entsprechenden
Dezimalstelle, Richtung Querstange geschoben wird)
Sind fünf Perlen im unteren Teil eines Stabes abgezählt → „Übertragung“ in
den oberen Bereich: Eine Fünfperle wird gesetzt, die fünf Einsperlen
zurückgeschoben
Sind beide oberen Perlen gezählt → „Übertragung“ auf eine Einerperle des
linken Nachbarstabes
Dezimalbrüche: „anwenderabhängig“, d.h. nur der momentane Benutzer
weiß, wo sich das Komma befindet (der Platz auf dem Abakus kann ja
beliebig gewählt werden)
Addition Subtraktion Multiplikation Division Radizieren
Die Addition
Einfaches Beispiel: 6+8
Gebe die 6 in den
Abakus ein
Gebe anschließend die
8 einfach hinzu
Addition Subtraktion Multiplikation Division Radizieren
Einfaches Beispiel: 6+8
Da sich nun zwei
Fünferperlen an der
Querverbindung
befinden, findet eine
„Übertragung“ in die
linke Spalte statt (mit
einer Einerperle)
Das Ergebnis kann sofort
abgelesen werden:14
Addition Subtraktion Multiplikation Division Radizieren
Beispiel mit Hilfskonstruktion: 27+39
Gebe die 27 in den
Abakus ein
Nun soll die 39 addiert
werden: Man fängt immer mit der
Einerstelle an (9).
Da die 9 jedoch nicht mehr (an
der Einerstelle) dargestellt werden
kann, greift man auf eine
Hilfskonstruktion zurück:
9=10-1
Addition Subtraktion Multiplikation Division Radizieren
Beispiel mit Hilfskonstruktion: 27+39
Addiere also erst 10 zur
27
Ziehe anschließend 1
wieder ab
Addition Subtraktion Multiplikation Division Radizieren
Beispiel mit Hilfskonstruktion: 27+39
Nun addiere 3 in der
Zehnerstelle
Auch hier muss wieder
die Hilfskonstruktion
angewendet werden: 3=5-2
Addiere also erst 5
Ziehe nun 2 wieder ab
Das Ergebnis kann sofort
abgelesen werden:66
Addition Subtraktion Multiplikation Division Radizieren
Zusammenfassung
Die Addition am „suan pan“ verläuft also analog zum
schriftlichen Addieren:
Als erstes werden die Einerstellen addiert, dann die Zehnerstellen usw.
Am zweiten Beispiel wird deutlich, dass auch mit Hilfskonstruktionen gearbeitet
werden kann.
Das geschieht, wenn nicht genügend Perlen an einer Stange zur Verfügung
stehen. So müssen dann die Werte durch passende Methoden dargestellt
werden (z.B.: 9=10-1, 3=5-2 usw.)
Anmerkung:
Die Addition von Dezimalbrüchen verläuft analog (hier kann
die Kommastelle frei gewählt werden)
Addition Subtraktion Multiplikation Division Radizieren
Die Subtraktion
Beispiel: 32-18
Gebe die 32 in den
Abakus ein
Auch hier fängt man wieder
mit der Einerstelle an: Da
die 8 jedoch nicht von der 2
abgezogen werden kann ->
Hilfskonstruktion: 8=10-2
Ziehe also erst 10 ab, d.h.
eine Perle bei der
Zehnerstelle
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 32-18
Addiere anschließend 2
Perlen an der Einerstelle
hinzu
Ziehe nun 10 (1Zehnerperle
wegnehmen) von 24 ab
Das Ergebnis kann
abgelesen werden: 14
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 1000-5
Gebe die 1000 in den
Abakus ein
Problem: an der
Einerstelle befinden
sich nun keine Perlen,
von denen man 5
abziehen könnte.
Idee: Die 1 an der
Tausenderstelle lässt sich auch
durch entsprechende Perlen an
der Hunderterstelle darstellen
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 1000-5
Zieht man nun in der
Hunderterspalte eine
Perle ab und addiert
gleichzeitig auf der
Zehnerstelle 10 dazu (eine 5- und
fünf 1-Perlen)…
…und zieht nun von den 10
auf der Zehnerstelle einen
ab und addiert auf der
Einerstelle 10
dazu….
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 1000-5
… kann man nun die 5
an der Einerstelle
abziehen
Das Ergebnis kann
abgelesen werden: 995
Addition Subtraktion Multiplikation Division Radizieren
Zusammenfassung
Wie auch bei der Addition werden hier jeweils Einerstellen von Einerstellen,
Zehnerstellen von Zehnerstellen usw. subtrahiert. Hier kommen die
Hilfskonstruktionen jedoch häufiger vor.
Im zweiten Beispiel wird klar, dass teilweise auch mit kleinen „Tricks“ gearbeitet
werden muss, wenn keine entsprechenden Perlen zur Verfügung stehen.
Addition Subtraktion Multiplikation Division Radizieren
Die Multiplikation
Beispiel: 58*3
Als erstes werden auf
der linken Seite des Abakus die
beiden Zahlen eingegeben.
Zwischen den beiden Zahlen wird
eine Stange als Platzhalter
freigelassen
(Grund: bessere Übersicht und
„Memory-Effekt“)
Nun multipliziert man die beiden
Einerstellen (8, 3) miteinander
und gibt das Ergebnis ganz rechts
am Abakus ein
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 58*3
Multipliziere nun die 5 mit 3.
Da man eigentlich 50*3
berechnet, trage also das
Ergebnis von 5*3 um eine Stange
nach links verschoben ein (also
zweite Stange von rechts)
Das Ergebnis kann
abgelesen werden: 174
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 284*73
Als erstes werden auf
der linken Seite des
Abakus wieder die
beiden Zahlen
eingegeben
Nun wird die 4 der 284 mit
der 3 der 73 multipliziert und
das Ergebnis (12) ganz
rechts eingegeben
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 284*73
Die 8 wird mit der 3 multipliziert
(eigentlich wieder 80*3) und das
Ergebnis rechts dazugegeben. Da
sich nun fünf Perlen im unteren
Bereich an der Zehnerstange
befinden, findet eine
„Übertragung“ in den oberen
Bereich statt
Ebenso wird nun die 2 mit der 3
multipliziert
Die Zahl, die nun abzulesen ist
(852), ist das Ergebnis der
Multiplikation 284*3
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 284*73
Mit der verbleibenden 7 der 73
wird nun ebenso verfahren wie
vorher:
das Produkt wird aber eine Spalte
weiter links (ab der Zehnerspalte)
eingegeben
Also: 4*7 ergibt 28, 8*7
ergibt 56 und 2*7 gibt 14
Da nun 852+280 gerechnet wird,
muss (zweimal) die
Hilfskonstruktion der Addition
angewendet werden
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 284*73
Das Ergebnis von 8*7
(eigentlich 80*70) kann
problemlos aufaddiert
werden
Beim Eintragen der 2*7
findet an dem
Tausenderstab wieder ein
Übertragung, hin zum
Zehntausenderstab, statt
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 284*73
Nun kann das Gesamtergebnis
abgelesen werden:
20732
Es kann vorkommen, dass
Zwischenergebnisse über
mehrere Stäbe hinausgehen, so
dass die (am Anfang eingegeben)
Zahlen ganz links „stören“. Diese
können dann entfernt werden
Addition Subtraktion Multiplikation Division Radizieren
Zusammenfassung
Auch bei der Multiplikation wird im Grunde genommen genauso verfahren wie
beim schriftlichen Multiplizieren:
Jede Ziffer der ersten (bzw. zweiten) Zahl muss mit allen Ziffern der zweiten
(bzw. ersten) Zahl multipliziert werden. Dabei muss man beachten, an welche
Stangen das Ergebnis eingegeben werden soll.
Die einzelnen Ergebnisse werden dann, ggf. unter Verwendung der
Hilfskonstruktionen, aufaddiert.
Addition Subtraktion Multiplikation Division Radizieren
Die Division
Beispiel: 182:14
Gebe zuerst wieder die beiden
Zahlen (182 und 14) links in den
Abakus ein. Achte dabei auf die
Reihenfolge: ganz links der
Divisor (14), daneben der
Dividend (182)
Verfahre nun wie bei der
schriftlichen Division…
… der Dividend wird von links
nach rechts „angegangen“…
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 182:14
Die 1 der 182 lässt sich
nicht durch 14 dividieren.
Deswegen nehme die 8
noch hinzu
Es lässt sich aller Voraussicht
nach ein zweistelliges Ergebnis
erwarten. Deswegen gebe an der
zweiten Stange von rechts nun
das (ganzzahlige) Ergebnis von
18:14 ein (1)
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 182:14
Nun wird die 1 mit der 14
multipliziert, das Ergebnis (14)
wird vom Dividend (182) von
vorne her (also von der 18)
abgezogen. Achtung: Hier muss
wieder mit der Hilfskonstruktion
gearbeitet werden!
Es bleibt nun also nur noch die
42. Diese lässt sich durch 14
teilen. Ergebnis ist 3. Gebe also
die 3 in den Abakus ein (ganz
rechts). Die 42 kann nun
„gelöscht“ werden.
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 182:14
Das Ergebnis kann der
Division 182:14 kann
nun abgelesen werden:
13
Zur Kontrolle kann noch
die Probe gerechnet werden
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 364:28
Gebe auch hier wieder Divisor
und Dividend in den Abakus
(ganz links) ein
Verfahre nun wie beim ersten
Beispiel:…
Die 3 der 364 kann durch die 2
der 28 geteilt werden. Das
Ergebnis (1) wird rechts in den
Abakus eingegeben. Da wieder
ein zweistelliges Ergebnis
erwartet wird, benutze wieder den
zweiten Stab von rechts
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 364:28
1*28 wird nun wieder von den ersten
beiden Ziffern der 364 abgezogen.
Vorsicht: 2 lässt sich bequem von der 3
abziehen. Bei der Rechnung „6-8“ gibt es
jedoch wieder ein Problem. Deswegen:
Hilfskonstruktion ;)
Als neuer Dividend wird jetzt die 84
angezeigt. Betrachtet man nun wieder die
beiden ersten Ziffern (die 8 der 84 und die
2 der 28), so würde sich ein Faktor von 4
ergeben (8 : 2 = 4). Da es sich aber mit
der 8 der 28 um eine größere Zahl als die
4 der 84 handelt, ist es angebracht, den
Faktor um 1 zu verringern. Es wird also
die 3 in die Spalte ganz rechts
eingetragen.
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: 364:28
Das Ergebnis von 3*28 wird nun
von 84 abgezogen. Diese
Rechnung ist nun nicht sonderlich
bequem im Kopf zu rechnen.
Zerlege also 3*28 wie folgt: 3*8 +
3*20. Dabei können die
Einzelergebnisse separat vom
Dividenden subtrahiert werden.
Es gilt also:
84 - (3*8) - (3*20) =
84-24-60 = 84-84 = 0
Das Ergebnis kann nun
abgelesen werden: 13
Addition Subtraktion Multiplikation Division Radizieren
Zusammenfassung
Am deutlichsten kann man sich die Abakus-Division analog zum schriftlichen Dividieren
darstellen:
Die einzelnen Rechnungen (Vielfachbildung und Subtraktion) werden dabei „im Kopf“ und aus
Platzgründen nicht am Abakus durchgeführt!
Sei xyz eine dreistellige Zahl (Dividend) und a der Divisor.
1. Fall: Der Quotient ist ohne Rest!
Teile nun x durch a. (falls dies nicht möglich ist, nehme y noch hinzu). Das maximale
ganzzahlige Vielfache (p*a) wird nun von x abgezogen. Zu diesem Ergebnis der Subtraktion nehme
nun y hinzu.
Teile auch hier wieder durch a. Das ganzzahlige Ergebnis q*a muss nun auch wieder
subtrahiert werden. Nehme nun zu diesem Ergebnis z hinzu. Diese Zahl ist ein
Vielfaches von a (r*a)
Sobald die (neue) Zahl nicht durch a teilbar ist und eine weitere Zahl hinzugenommen
werden muss, wird an ansprechender Stelle beim Quotient eine 0 ergänzt
So weit so gut: Am Abakus werden der Reihe nach (rechts am Abakus) die einzelnen
Zahlen p,q,r eingegeben. Die Subtraktionsschritte dieser Vielfachen von a können (unter
ggf. Verwendung der Hilfskonstruktion) vom Divisor subtrahiert werden.
2. Fall: Der Quotient ist mit Rest!
Geht die letzte Subtraktion r*a nicht „glatt“ auf, so ergänze zu diesem Rest eine 0. Beim Quotienten
wird nun an entsprechender Stelle ein Komma gesetzt. Die Stelle des Komma muss sich am Abakus
gemerkt werden.
Addition Subtraktion Multiplikation Division Radizieren
Die Quadratwurzel einer Zahl kann durch einfache
Subtraktion herausgefunden werden, wobei der Abakus als
„Strichliste“ angesehen werden kann:
Die Quadratwurzel einer Zahl kann herausgefunden
werden, indem nacheinander 1, dann 3, dann 5 (also die
ungeraden Zahlen) von der Zahl abgezogen werden, bis
die 0 erreicht ist.
Die Quadratwurzel dieser Zahl ist die Anzahl der
Subtraktionen.
Die Anzahl der einzelnen Subtraktionsrechnungen werden
schrittweise in den Abakus eingegeben.
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: √36
Die „root no.“ wird von der „square no.“ abgezogen:
Root No.
1
3
5
7
9
11
Square No.
36
35
32
27
20
11
0
Wir mussten also 6 mal die Subtraktion anwenden.* D.h. die
Quadratwurzel von 36 ist 6.
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: √1024
Bei größeren Zahlen ist es natürlich mühselig, viel Subtraktionen
durchzuführen.
Verfahre hier dann wie folgt:
Zerlege die Zahl in Zahlenpaare (10 und 24)
Verfahre mit dem ersten Zahlenpaar (10) wie oben, bis die „Root No.“
größer ist, als die „Square No.“.
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: √1024
Root No.
1
3
5
Square No.
10
24
9
6
1
Nun ist: 5>1
Multipliziere nun die letzte „Root No.“ mit 10
und addiere 11.
5*10+11 = 61
Nehme nun das zweite Zahlenpaar (24) hinzu und fahre mit
der Subtraktion fort…
Addition Subtraktion Multiplikation Division Radizieren
Beispiel: √1024
Root No.
61
63
Square No.
124
63
0
Nun muss noch folgende Rechnung durchgeführt werden:
(63+1) 2 = 32
(*:Dieser Schritt kann übrigens genauso beim ersten Beispiel
durchgeführt werden: (11+1)/2 = 6 )
Das Ergebnis für √1024 ist also 32
Addition Subtraktion Multiplikation Division Radizieren
Zusammenfassung
Bei kleineren Zahlen (wie im Beispiel 1) lässt sich die Quadratwurzel auf folgende Weise
finden:
Ziehe nacheinander 1,3,5,…2*n+1 (Bezeichnung: „root no.“) vom Radikanden (y) ab. Sei
x nun die „root no.“ deren Subtraktion 0 ergibt:
Es gilt: (x+1)/2 = √y
(Außerdem ist die Anzahl der durchzuführenden Subtraktionen ebenfalls die gesuchte
Wurzel)
Die Quadratwurzel für größere Zahlen kann einfacher und schneller gefunden werden,
indem man den Radikanden (y) in Zahlenpaare (von rechts aus) unterteilt (Beispiel 2).
Verfahre dann wie folgt:
a.) Führe die Subtraktionen für das linke Zahlenpaar (wie oben) durch, bis die „root no.“
größer als die „square no.“ ist.
b.) Multipliziere diese letzte „root no.“ mit 10 und addiere anschließend 11 dazu.
c.) Ergänze nun diese „square no.“ mit dem zweiten Zahlenpaar des Radikanden und fahre mit der
Subtraktion wie gewohnt fort.
d.) Sei x nun die „root no.“ deren Subtraktion 0 ergibt. Dann gilt:
(x+1)/2 = √y
Ergibt der letzte Subtraktionsschritt eine negative Zahl (anstatt 0) so ist die gesuchte
Quadratwurzel ein Dezimalbruch.
Literaturhinweise
Falls ihr nun Interesse bekommen habt, mit dem chinesischen Abakus
(suan pan) zu arbeiten, bzw. ihn in der Schule einzusetzen, könnt ihr
auch noch in folgenden Büchern das Grundwissen vertiefen (z.B. wird
hier erklärt, wie Kubikwurzeln gezogen werden können!)
•
•
Maxwell, R. Perceval: How to use the chinese Abacus - Kings
Langley: Maxwell, 1979
Moon, Perry: The Abacus. Ist history; ist design; ist possibilities in the
modern world – New York: Gordon and Breach, 1971
Für den Umgang mit einem „Schulabakus“ empfehle ich:
•
Johann, Michael & Matros Norbert: Wechselspiele. Kreatives Rechnen
am Schulabakus – Landau: Knecht, 2001