Addition und Subtraktion ganzer Zahlen an der Zahlengeraden

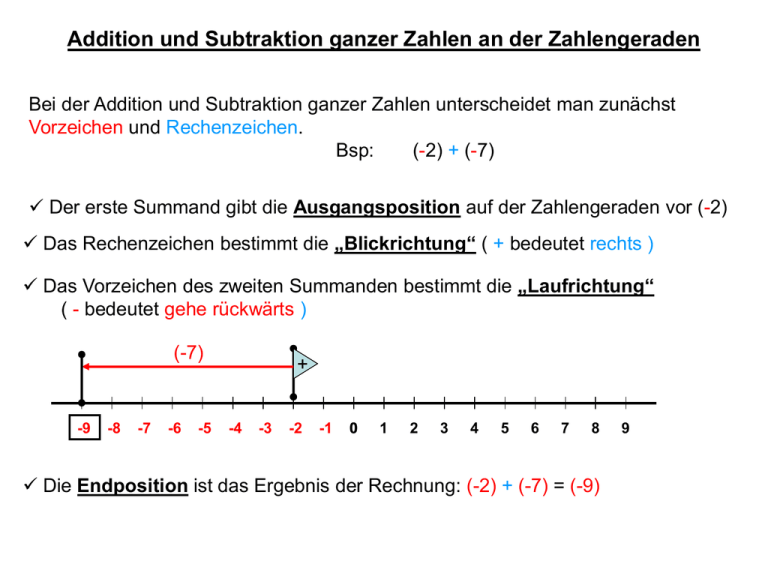
Addition und Subtraktion ganzer Zahlen an der Zahlengeraden
Bei der Addition und Subtraktion ganzer Zahlen unterscheidet man zunächst
Vorzeichen und Rechenzeichen.
Bsp:
(-2) + (-7)
 Der erste Summand gibt die Ausgangsposition auf der Zahlengeraden vor (-2)
 Das Rechenzeichen bestimmt die „Blickrichtung“ ( + bedeutet rechts )
 Das Vorzeichen des zweiten Summanden bestimmt die „Laufrichtung“
( - bedeutet gehe rückwärts )
(-7)
-9
-8
-7
-6
-5
+
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
 Die Endposition ist das Ergebnis der Rechnung: (-2) + (-7) = (-9)
9
Addition und Subtraktion ganzer Zahlen an der Zahlengeraden
Weitere Beispiele für die Addition (+ bedeutet Blick nach rechts)
Bsp:
(-2) + (+3) = (+1)
(+2) + (+3) = (+5)
(+9) + (-3) = (+6)
(- bedeutet gehe rückwärts)
(+3)
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
(+3)
1
2
3
4
(-3)
5
6
7
8
9
Addition und Subtraktion ganzer Zahlen an der Zahlengeraden
Beispiele für die Subtraktion (- bedeutet Blick nach links)
Bsp:
(-2) - (+3) = (-5)
(+2) - (+3) = (-1)
(+6) - (-3) = (+9)
(- bedeutet gehe rückwärts)
(+3)
-9
-8
-7
-6
-5
-4
-3
(+3)
-2
-1
0
1
(-3)
2
3
4
5
6
7
8
9
Addition und Subtraktion ganzer Zahlen an der Zahlengeraden
Wir führen jetzt jeweils die Gegenoperation mit der Gegenzahl durch:
Bsp:
(-2) - (+3) = (-5)
(+2) - (+3) = (-1)
(+6) - (-3) = (+9)
(-2) + (-3) = (-5)
(+2) + (-3) = (-1)
(+6) + (+3) = (+9)
Und stellen fest, dass wir eine Rechenoperation mit einer beliebigen Zahl
durch die Gegenoperation mit der Gegenzahl ersetzen können.
Das Ergebnis bleibt gleich.
-9
-8
-7
-6
-5
(-3)
(-3)
(+3)
(+3)
(+3)
(-3)
-4
-3
-2
-1
0
Beispiele: (+2) - (+3) = (+2) + (-3) = -1
1
2
3
4
5
6
7
8
9
Addition und Subtraktion ganzer Zahlen an der Zahlengeraden
Wir vereinfachen jetzt die Schreibweise, indem wir positive Vorzeichen und
Klammern um positive Zahlen weglassen.
Bsp:
Bsp:
(-2) - (+3) = (-5)
(+2) - (+3) = (-1) (+6) - (-3) = (+9)
(-2) + (-3) = (-5)
(+2) + (-3) = (-1) (+6) + (+3) =(+9)
-2 - 3 = -5
-2 + (-3) = -5
2 - 3 = -1
2 + (-3) = -1
6 - (-3) = 9
6+3=9
Immer noch gilt, dass das Ergebnis gleich bleit, wenn man eine
Subtraktion, durch eine Addition mit der Gegenzahl ersetzt.