Winkelfunktionen - Mathematische Hintergründe
Werbung

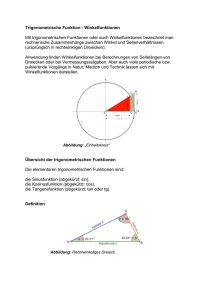
Winkelfunktionen Zusammenfassung: Winkelfunktionen drücken einfache geometrische Beziehungen zwischen Winkeln und Längen(verhältnissen) aus. Ihre Schwierigkeit insbesondere für AnfängerInnen besteht darin, dass sie über die bisher bekannten Rechenoperationen hinaus weisen. Stichworte: Sinus und Cosinus | Sinus-Cosinus-Rechner | Sinus und Cosinus im rechtwinkeligen Dreieck | Sinus und Cosinus für alle Winkel: Zeigerdiagramme | Vorzeichen von Sinus und Cosinus | Wertebereich von Sinus und Cosinus | Eigenschaften von Sinus und Cosinus | Der Satz des Pythagoras | Periodizität und (Anti-)Symmetrie | Identitäten mit Supplementär- und Komplementärwinkeln | Doppelte Winkel | Summensätze (Additionstheoreme) für Sinus und Cosinus | Tangens und Cotangens | Tangens-Cotangens-Rechner | Tangens und Cotangens im rechtwinkeligen Dreieck | Tangens und der Anstieg | Eigenschaften von Tangens und Cotangens | Summensätze für Tangens und Cotangens | Weitere Winkelfunktionen | Spezielle Winkel | Das Bogenmaß | Winkelmaße | Das Gradmaß | Radiant | Kleine Winkel | Die inversen Winkelfunktionen (ArcusFunktionen) | Ebene Polarkoordinaten | Polarwinkel | Winkelfunktionen am Computer | Neugrad | gon | Ausblicke Sinus und Cosinus en wir mit einer harmlosen Frage: Wie lange ist der Schatten eines um den Winkel v zur Horizontalen geneigten Stabes der Länge 1, wenn die Sonne senkrecht auf abscheint? Betrachten Sie die nebenstehende Skizze: Die rote Strecke stellt den r, der Pfeil symbolisiert das von oben einfallende Licht.Der Winkel soll beliebig werden können (im Beispiel rechts ist = 51°). Gesucht ist die Länge der grünen . er Stelle tritt eine Überraschung auf, die viele Lernende vor eine völlig neue n stellt, und die mit den Schwierigkeiten, die die Winkelfunktionen vielen Menschen n, zusammenhängt: Das Problem ist nicht mit Hilfe der Rechenoperationen, die wir kennengelernt haben, zu lösen! Nur in Ausnahmefällen ist die Länge des Schattens ereits bekannte "schöne" Zahlen auszudrücken (z.B. für = 60° ist sie 1/2, für ist sie 21/2), aber etwa für = 51° ergibt sich eine (reelle) Zahl, die sich nicht in oder einer ähnlichen Weise angeben lässt. Wir können das hier nicht begründen, ist wichtig, es zu wissen, um die Vorgangsweise, die wir nun beschreiten werden, Funktion zu verstehen. Obwohl wir zunächst nicht wissen, wie wir die Länge des Schattens für (beispielsweise) = 51° berechnen können, ist klar, dass sie durch die Fragestellung eindeutig bestimmt ist. Um eine grobe Näherung zu erhalten, können wir eine (möglichst) genaue Zeichnung nach Art der obigen Skizze anfertigen und die Länge der grünen Strecke abmessen. Es ergibt sich ein Wert von ungefähr 0.63. Ein solches Verfahren ist aber vom mathematischen Standpunkt aus betrachtet unbefriedigend. Was wir allerdings in jedem Fall tun können, ist, dem genauen Resultat einen Namen zu geben: wir nennen es Cosinus. Die Länge der grünen Strecke wird als cos oder, mit Klammer, als cos() geschrieben und "Cosinus alpha" oder "Cosinus von alpha" ausgesprochen. Da der Schatten die Länge des Bildes ist, das die Sonne auf den Boden "projiziert", können wir formulieren: cos ist die Länge der Projektion einer Strecke, die wie in der linksstehenden Skizze um den Winkel geneigt ist und die Länge 1 hat. Ist = 51°, wie in unserem Beispiel, so schreiben wir cos(51°). Das Symbol cos(51°) stellt also eine reelle Zahl dar (sie ist ungefähr 0.63), cos(60°) stellt eine andere reelle Zahl dar (nämlich 1/2), usw. nalog dazu können wir den Stab mit horizontal einfallendem Licht beleuchten und wie lange sein auf eine senkrechte Wand geworfener Schatten ist. Auch diese ässt sich im Allgemeinen nicht mit Hilfe der uns bereits bekannten methoden angeben, und wir nennen sie Sinus. ge der blauen Strecke in der rechtsstehenden Skizze wird als sin oder, mit er, als sin() geschrieben und "Sinus alpha" oder "Sinus von alpha" prochen. Wieder handelt es sich um eine Projektion, diesmal allerdings entlang tal einfallender Lichtstrahlen. sin kann auch als die scheinbare Länge, unter den roten Stab aus großer Entfernung vor seinem Hintergrund sehen, gedeutet . Ist beispielsweise = 51°, so schreiben wir sin(51°). nd Cosinus (und einige andere Größen, die wir weiter unten daraus gewinnen ) heißen Winkelfunktionen oder trigonometrische Funktionen. Die hnung "Funktionen" rührt daher, dass jedem Winkel die beiden Zahlen sin s zugeordnet werden. Mathematisch betrachtet ist das nichts Aufregendes. Wenn wir einer Zahl x ihr Quadrat zuordnen s als f(x) = x2 schreiben, tun wir im Prinzip nichts anderes. Der Unterschied zum Quadrieren besteht nur darin, dass die sche Berechnung von sin und cos für einen gegebenen Winkel aufwendiger ist als das Quadrieren einer nen Zahl. Zum Glück können wir diese Arbeit Werkzeugen überlassen, die das für uns tun, z.B. dem Computer oder dem nrechner. Auch diese Werkzeuge liefern für die meisten Winkel nur numerische Näherungswerte, die aber, ähnlich wie urzelziehen, für praktische Anwendungen ausreichend genau sind. en Sie also, zu akzeptieren, dass Sie die Art und Weise, wie Rechenmaschinen das machen, in diesem Kapitel nicht lernen werden. Das hindert uns aber nicht daran, diese Werkzeuge zu benutzen: sin ( ° ) cos ( ° ) Sie einige Winkel ein und klicken Sie auf die Buttons mit den Gleichheitszeichen, um deren Sinus und Cosinus anzeigen en! Wir können nun auch das obige Beispiel ( = 51°) mit hoher Genauigkeit lösen: Unsere kleine Rechenmaschine sagt ss cos(51°) = 0.6293203910498375 ist, und das ist die gesuchte Länge des Schattens, den das senkrecht einfallende licht am Boden wirft. Genau genommen ist auch das nur ein Näherungswert, aber für alle praktischen Zwecke ist er sogar au. Hat der rote Stab etwa eine Länge von einem Meter, so können wir die Länge seines Schattens getrost als 62.9 cm n. nd Cosinus (letzterer manchmal auch "Kosinus" geschrieben), sowie alle weiteren Winkelfunktionen, die Sie in diesem noch kennenlernen werden, spielen in der Mathematik und in zahlreichen Anwendungen eine wichtige Rolle. Ihre ende Bedeutung rührt letzten Endes daher, dass sie einfachen und sehr allgemeinen (d.h. oft auftretenden) rischen Fragestellungen entspringen. Dass ihre numerische Berechnung keine leichte Sache ist und zunächst an terwerkzeuge oder Taschenrechner delegiert wird, mag zwar ein bisschen lästig erscheinen, sollte aber die Tatsache ihrer ellen Einfachheit (und Schönheit, wie viele MathematikerInnen sagen würden) nicht verdecken. Sinus und Cosinus im rechtwinkeligen Dreieck Zum Seiten sen nun im Prinzip, was der Sinus und der Cosinus eines Winkels sind und sehen uns nun Dinge an, die wir damit anstellen können. In jeder der Grafiken des vorigen Abschnitts en wir ein rechtwinkeliges Dreieck: In der rechtsstehenden Grafik haben wir es ehoben. Außerdem haben wir das Ganze ein bisschen gedreht, denn auf die Lage des s in der Zeichenebene kommt es nicht an. Mit Hilfe dieser Grafik können wir unsere Winkelfunktionen auf eine andere Weise charakterisieren: m rechtwinkeligen Dreieck, dessen Hypotenuse die Länge 1 hat, sei chten Winkel. Dann ist einer der beiden sin die Länge der Kathete, die dem Winkel gegenüberliegt, und cos die Länge der Kathete, die dem Winkel anliegt. Nun betrachten wir ein rechtwinkeliges Dreieck, das denselben Winkel besitzt, dessen Hypotenuse aber nicht unbedingt die Länge 1 hat. Wir erhalten es, indem wir unser bisheriges Dreieck "aufblasen" oder "schrumpfen", und zwar so, dass alle Winkel erhalten bleiben. Das ursprüngliche und das links abgebildete Dreieck sind einander ähnlich. In beiden Dreiecken ist die (dem Winkel ) gegenüberliegende Kathete (blau) um den Faktor sin kürzer als die Hypotenuse, und in beiden Dreiecken ist die Ankathete (grün) um den Faktor cos kürzer als die Hypotenuse. In diesem Sinn können sin und cos als Verkürzungsfaktoren verstanden werden. Dieser Sachverhalt kann formal mit Hilfe des Strahlensatzes bewiesen werden. Wir sehen also, dass in jedem rechtwinkeligen Dreieck gilt: sin = Gegenkathete (1) Hypotenuse cos = Ankathete (2) Hypotenuse Ähnlichke Strahlen Themen a klassisc Geome h diese Formeln besser merken zu können, ziehen Sie am besten folgende "Eselsbrücke" heran: Der Sinus gehört zur eberliegenden Kathete, der Cosinus zur onliegenden Kathete. In den meisten Lehrbüchern werden Sinus und Cosinus ie Eigenschaften (1) und (2) eingeführt. Mit Hilfe des nebenstehenden Applets, in dem ebenfalls (1) und (2) als gspunkte genommen werden, können Sie sich mit Beziehungen ein bisschen besser vertraut machen. Apple Definitio Winkelfunk llustrieren, wie diese Eigenschaften beim Rechnen det werden, betrachten wir folgende ssungsaufgabe: Wie in nebenstehender Skizze ellt, wird die direkte Entfernung einer htungsstation zu einem Berggipfel mit 3.7 km sen. Der Gipfel erscheint unter einem Höhenwinkel von Wie hoch ist der Berg? g: Erkennen Sie das rechtwinkelige Dreieck in der Skizze? Wir wenden die Beziehung (1) an: h sin (19.5°) = . 3.7 km st h = sin(19.5°) × 3.7 km. Unter Zuhilfenahme der obigen Rechenmaschine ergibt sich sin(19.5°) = 0.3338, daher 338 × 3.7 km = 1.24 km, wobei wir das Resultat in vernünftiger Weise gerundet haben. Sie derartige Aufgaben lösen, empfiehlt es sich, einen Rechner (z.B. einen Taschenrechner, den mathe online Minir oder JavaCalc) bereitzuhalten. Am Ende dieses Kapitel finden Sie ein paar Tipps zum computerunterstützten Rechnen kelfunktionen. Sinus und Cosinus für alle Winkel: Zeigerdiagramme oben gegebenen Definitionen von Sinus und Cosinus sind genau men noch nicht ganz vollständig. Erinnern wir uns: Wir haben Sinus und s eingeführt als die Längen der Schatten eines geneigten Stabes der 1, einmal unter vertikalem Lichteinfall (cos ) und einmal unter talem Lichteinfall (sin ). In der nebenstehenden Skizze ist das noch dargestellt, wobei wir den (roten) Stab aber diesmal mit einem Ende in den ng eines rechtwinkeligen Koordinatensystems gehängt haben und die en" (oder Projektionen) entlang der Achsen einzeichnen. Der Winkel ativ zur horizontalen Achse (x-Achse) im Gegenuhrzeigersinn gemessen. hen wir, dass wir den Winkel vergrößern können, indem wir den roten e einen Uhrzeiger (allerdings gegen den Uhrzeigersinn) drehen. Das Ende des Zeigers beschreibt dadurch einen Kreisbogen (mit Radius 1). len solche Diagramme als "Zeigerdiagramme" bezeichnen. Zum Seiten Sinus und C und ih für alle W Quadran Die Drehung des Zeigers kann über die vertikale Lage hinaus fortgesetzt werden. Eine solche Lage des Zeigers beschreiben wir, wie in der linksstehenden Skizze dargestellt, mit einem Winkel, der größer als 90° ist. Wir können nun auch hier (analog zur obigen Skizze) die Projektionen auf die Achsen einzeichnen und dadurch Sinus und Cosinus für Winkel größer als 90° definieren. Dabei kommen wir überein, eine vom Ursprung nach links oder nach unten weisende Strecke als negativ zu zählen. Der im Beispiel links eingestellte Winkel ist 131°. Die Länge der grünen Strecke ist ungefähr 0.656. Der Cosinus dieses Winkels ist daher ungefähr 0.656, also negativ! Probieren Sie es selbst mit Hilfe der obigen Rechenmaschine aus! sin(131°) hingegen ist positiv (ungefähr 0.755), da die blaue Strecke vom Ursprung aus nach oben weist. Wenn wir den roten Zeiger weiterdrehen, können wir jeden Winkel zwischen 0° und 360° einstellen, und in all diesen Fällen legt unsere Vorschrift ganz eindeutig fest, wie groß Sinus und Cosinus sind und welche Vorzeichen sie haben. Der Button rechts ruft eine Übersicht über alle dabei auftretenden Vorzeichenkombinationen auf. Die Vorzeichen von Sinus und Cosinus hängen davon ab, in welchem der vier Quadranten der Zeiger, der den Winkel ntiert, liegt. (Die Quadranten teilen die Zeichenebene in vier Bereiche ein, die von den Achsen begrenzt werden. Sie im Gegenuhrzeigersinn von 1: "rechts oben" über 2: "links oben" und 3: "links unten" bis 4: "rechts unten" gezählt). nen den Zeiger sogar noch weiterdrehen, wobei dann allerdings nichts Neues mehr auftritt: Ein Winkel von 370° heidet sich nicht von 10° dementsprechend sind auch die Winkelfunktionen gleich, z.B. sin(370°) = sin(10°). Wir können ger auch zurückdrehen und wieder verkleinern, bis wir zu negativen Zahlen gelangen. Aber auch das bringt nichts Ein Winkel von 10° unterscheidet sich nicht von 350° dementsprechend sind auch die Winkelfunktionen gleich, z.B. °) = sin(350°). Unsere Rechenmaschine weiß das auch probieren Sie es! wollen wir Sinus und Cosinus für alle Winkel definieren, und wieso tun wir es auf diese Weise? Vor allem, weil es für viele praktisch ist. Winkel zwischen 90° und 180° (sogenannte "stumpfe" Winkel, im Gegensatz zu "spitzen" Winkeln zwischen 90°) treten auch in der Praxis auf. Und wenn der rote Zeiger nach rechts weist und um 1° nach unten geneigt ist, so ist die 1° kürzer (und auch für die Vorstellung günstiger) als 359°. Diese Konvention hat aber auch theoretische uenzen. So ist zum Beispiel die Summe zweier Winkel wieder ein Winkel. Sind und zwei Winkel (d.h. beschreiben igerstellungen), so ist + wieder ein Winkel, da ja jeder Wert zulässig ist. Wir müssen dabei nur bedenken, dass die sich um 360° (oder Vielfache davon) unterscheiden, miteinander identifiziert werden. im nächsten Abschnitt sehen werden, lassen sich mit Hilfe der Zeigerdiagramme zahlreiche grundlegende Eigenschaften kelfunktionen mühelos beweisen. Diese Diagramme stellen eine wertvolle Hilfe dar, und es lohnt sich, sie im Gedächtnis alten. Im nebenstehenden Applet können Sie den Winkel interaktiv verändern und sich die Sache dynamisch ansehen. hte Teil des Applets zeigt eine graphische Darstellung der Winkelfunktionen, die einem späteren Kapitel vorbehalten ist, aber vielleicht jetzt schon interessant finden (ansonsten ignorieren Sie sie einfach). Apple Die Graph sin, cos u r Eigenschaften, die aus den Zeigerdiagrammen hervorgehen, betrifft den Wertebereich von Sinus und Cosinus: Die dieser beiden Funktionen können nie kleiner als 1 oder größer als 1 sein. Das folgt unmittelbar daraus, dass die onen des Zeigers auf die Achsen nicht länger als er selbst (der ja die Länge 1 hat) sein können. Wir können also eren, dass für alle Winkel 1 sin 1 und 1 cos 1 (3) ssen Sie bereits ziemlich viel über die Winkelfunktionen Sinus und Cosinus. Der nebenstehende Button ruft zwei Beispiele ehbewegung und die harmonische Schwingung) auf, die illustrieren, wie wichtig diese Konzepte für die Physik sind. Zwei Beis physikalis Eigenschaften von Sinus und Cosinus Zum Seiten nkelfunktionen Sinus und Cosinus zählen zu den wichtigsten mathematischen Funktionen überhaupt. Sie besitzen he Eigenschaften, die sowohl in Anwendungen wie auch in der reinen Mathematik benötigt werden. Von einigen dieser chaften soll jetzt die Rede sein. Der Satz des Pythagoras ht werden Sie überrascht sein, hier einen alten Bekannten zu treffen: den pythagoräischen z! Betrachten wir wie zu Beginn dieses Kapitels ein rechtwinkeliges Dreieck, dessen nuse die Länge 1 hat. Nebenstehend ist eine der bereits oben verwendeten Grafiken gegeben. (Solche Dreiecke sind auch in den Zeigerdiagrammen des vorigen Abschnitts enthalten). z des Pythagoras besagt, dass im rechtwinkeligen Dreieck die Summe der Quadrate der n(längen) gleich dem Quadrat der Hypotenuse(nlänge) ist. Auf das nebenstehende Dreieck andt bedeutet das, dass für jeden Winkel die Identität sin2 + cos2 = 1 (4) bei ist sin2 eine Kurzschreibweise für (sin )2, gesprochen: "Sinus-Quadrat ". Diese Formel ist nderes als eine zu Beginn vielleicht ungewöhnliche Art, den Pythagoräischen Satz auszudrücken. Sie zeigt einen en Zusammenhang zwischen Sinus und Cosinus auf. Ist etwa für irgendeinen Winkel sin bekannt, so gilt ________ cos = ± 1 sin2 , as Vorzeichen davon abhängt, in welchem Quadranten der Zeiger, der den Winkel m ersten und vierten Quadranten +, ansonsten ). (5) im Zeigerdiagramm repräsentiert, Periodizität und (Anti-)Symmetrie n Zeigerdiagrammen ergibt sich, dass Sinus und Cosinus periodische Funktionen sind: Wird zu einem Winkel 360° addiert, so ist der Zeiger in derselben Position wie für . Daher gilt sin( + 360°) = sin cos( + 360°) = cos . der volle (6) Periodiz en auch: Die Periode (oder Periodenlänge) dieser beiden Funktionen ist 360°. Weiters gilt sin() = sin cos() = cos , (7) (Anti)Sym b der Sinus als antisymmetrische, der Cosinus als symmetrische Funktion bezeichnet wird. (Die volle Bedeutung dieser Begriffe wird erst in einem späteren Kapitel klar werden). Identitäten mit Supplementär- und Komplementärwinkeln weitere nützliche Identitäten ergeben sich für Winkel, die einander zu 90° (Komplementärwinkel) oder 180° mentärwinkel) ergänzen, und solche, die sich um 90° oder 180° unterscheiden: sin(90° ) = cos cos(90° ) = sin sin( + 90°) = cos cos( + 90°) = sin sin(180° ) = sin cos(180° ) = cos sin( + 180°) = sin cos( + 180°) = cos . (8) (9) (10) (11) rte von Sinus und Cosinus für beliebige Winkel ergeben sich also ganz einfach aus jenen für Winkel zwischen 0° und 90°. Doppelte Winkel sere beiden Winkelfunktionen für einen Winkel bekannt, so sind sie für den doppelten Winkel durch sin(2) = 2 sin cos (12) cos(2) = cos2 sin2 (13) n. Wir beweisen diese beiden Formeln hier nicht. Sie sind Spezialfälle der im nächsten Punkt zu besprechenden ten. Summensätze (Additionstheoreme) für Sinus und Cosinus ch zu den bisher besprochenen Beziehungen zwischen Sinus und Cosinus gelten einige weitere Identitäten, die zwei ge) Winkel enthalten, und die einer gewissen (mathematischen) Schönheit nicht entbehren. Sie sind unter dem Namen ensätze oder Additionstheoreme bekannt. Wir verzichten hier darauf, sie zu beweisen (das geschieht am bequemsten men der Komplexen Zahlen), sondern geben sie lediglich wieder. Für zwei beliebige Winkel und gilt immer sin( + ) = sin cos + cos sin (14) cos( + ) = cos cos sin sin (15) Beweis m komplexer wir = , so erhalten wir (12) und (13). Weiter unten werden wir die Summensätze für zwei andere Winkelfunktionen en. Weite Eigenschaften dieser beiden Winkelfunktionen können Sie mit Hilfe des nebenstehenden Buttons aufrufen. Ihre exakten ür einige spezielle Winkel sind in einem späteren Abschnitt aufgelistet. Mehr Informationen finden Sie in einschlägigen sammlungen, z.B. im Abschnitt Trigonometrische Funktionen von DeskTop Mathematik oder im Abschnitt Trigonometrie thematik.net. Tangens und Cotangens von Sinus Cosin Zum Seiten Sinus und Cosinus sind noch einige andere Funktionen, die von ihnen abgeleitet sind, gebräuchlich. Insbesondere men die Quotienten aus Sinus und Cosinus eigene Namen: Tangens und Cotangens (letzterer manchmal auch gens" geschrieben). Wir definieren: sin tan = (16) cos cos cot = 1 = sin Apple Definitio Winkelfunk tan . (17) en Sie, dass diese beiden Ausdrücke die Kehrwerte voneinander sind, also eng zusammenhängen: ihr Produkt ist 1. (Auf en Taschenrechnern findet sich gar keine Taste für den Cotangens, da er als 1/Tangens berechnet werden kann). mal werden statt tan und cot die Abkürzungen tg und ctg verwendet. Hier eine kleine Rechenmaschine für diese beiden unktionen: tan ( ° ) cot ( ° ) erschied zu Sinus und Cosinus sind Tangens und Cotangens für einige Winkel nicht definiert: Berechnen Sie sweise tan(90°) oder cot(0°). Unser Rechner gibt "Infinity" aus, womit er anzeigt, dass eine Division durch Null versucht ist. Aus den Definitionen (16) und (17) können wir auch den Grund dafür erkennen: Ist cos = 0 (was für = 90° und 270° passiert, letzteres ist mit 90° gleichbedeutend), so verschwindet der Nenner in (16). In diesen Fällen ist tan nicht definiert, und es gilt cot = 0. Ist sin = 0 (was für = 0° und ±180° passiert), so verschwindet der Nenner in (17). In diesen Fällen ist cot nicht definiert, und es gilt tan = 0. ten liefert unser Rechner konkrete Zahlenwerte, die nun allerdings beliebig groß werden können. Tangens und Cotangens im rechtwinkeligen Dreieck angens und Cotangens treten als Seitenverhältnisse in jedem rechtwinkeligen Dreieck auf. Mit r Definitionen (16) und (17) ergibt sich aus (1) und (2) tan = Gegenkathete (18) Ankathete cot = Ankathete (19) Gegenkathete wir uns als Anwendungsbeispiel eine kleine Vermessungsaufgabe an: Der Gipfel eines 1.24 km hohen Berges wird unter Höhenwinkel von 19.5° gesehen. Wie weit ist der Beobachter vom Fußpunkt des Gipfels entfernt? g: Erkennen Sie das rechtwinkelige Dreieck in der Skizze? Wir wenden die Beziehung (18) an: 1.24 km tan (19.5°) = . d st d = 1.24 km/tan(19.5°). Unter Zuhilfenahme des obigen Tangens-Cotangens-Rechners ergibt sich tan(19.5°) = 0.3541, = 1.24 km/0.3541 = 3.502 km (wobei der abermals gerundete Wert d = 3.50 km für die meisten Zwecke ausreichen wird). Praxis werden Sie übrigens nicht zuerst tan(19.5°) berechnen und danach erst die Division ausführen, sondern wenn es hner oder das verwendete Programm zulässt gleich die gesamte Anweisung zur Berechnung von 1.24/tan(19.5°) en. (Zur Verwendung elektronischer Rechenhilfen sagen wir weiter unten mehr). Tangens und der Anstieg Dem Tangens kommt eine ganz besondere Stellung zu, da er den Zusammenhang zwischen dem Steigungswinkel und dem Anstieg (der Steigung) einer Geraden ausdrückt. Um den Anstieg einer Geraden zu bestimmen, wird, wie in der nebenstehenden Skizze dargestellt, ein "Steigungsdreieck" gezeichnet. Der Quotient k = y/x wird als Anstieg der Geraden bezeichnet er hat in allen Steigungsdreiecken denselben Wert, unabhängig von ihrer Größe. Definition (18) sagt uns dann, dass der Anstieg gleich dem Tangens des Steigungswinkels ist: k = tan . Anstie einer Ger (20) beispielsweise der Steigungswinkel einer Straße 12°, so ist ihr Anstieg tan(12°), was näherungsweise 0 .21 ist. Die rstafel, die die Steigung der Straße anzeigt, wird dann die Aufschrift "21%" tragen (was als "21 Meter Höhenunterschied Meter laut Straßenkarte zurückgelegter Entfernung" gelesen werden kann). Für eine senkrechte Gerade ist der Anstieg nvolles Konzept, was genau der Tatsache, dass tan(90°) und tan(90°) nicht definiert sind, entspricht. Apple Der Anstie Gerad Eigenschaften von Tangens und Cotangens n für Sinus und Cosinus aufgelisteten Beziehungen implizieren eine ützlicher Eigenschaften von Tangens und Cotangens. Wie Sinus und s lassen sie sich in Zeigerdiagrammen geometrisch interpretieren. tehend ist ein solches Diagramm abgebildet. Der Winkel wird durch en) Zeiger repräsentiert. Der Tangens dieses Winkels kann als Abschnitt hellblau eingezeichneten Geraden g (der sogenannten Tangense) abgelesen werden. Er ist, wie sich aus der Beziehung (20) ergibt, der des Zeigers, der in der Skizze durch eine strichlierte Linie bis zur s-Schiene fortgesetzt wurde. Auch für Winkel größer als 90° und für e Winkel wird der Tangens an derselben Geraden g abgelesen. Mit dieser e kann auch sein Vorzeichen für derartige Winkel leicht ermittelt werden. 90° und = 90° ist der Zeiger parallel zur Tangens-Schiene. Hier wir den geometrischen Grund dafür, dass der Tangens für diese Winkel efiniert ist. Sehen Sie sich die Sache auch im linken Teil des tehenden Applets an. Für den Cotangens gilt Analoges, wobei lediglich e der Achsen vertauscht werden muss. Apple Die Graph sin, cos u e: Zeichnen Sie Sinus, Cosinus und Tangens in ein einziges iagramm ein. Versuchen Sie, anhand dieses Diagramms zu beweisen, er Abschnitt auf der Tangens-Schiene tatsächlich die in (16) definierte Größe ist. (Tipp: Es treten zwei zueinander ähnliche e auf). us und Cosinus sind Tangens und Cotangens periodische Funktionen; allerdings ist die Periode für sie kürzer sie 180°: tan( + 180°) = tan cot( +180°) = cot . (21) eihe weiterer Eigenschaften (unter anderen die Summensätze für Tangens und Cotangens) können Sie mit Hilfe des tehenden Buttons aufrufen. Die exakten Werte der beiden Funktionen für einige spezielle Winkel sind weiter unten tet. Für mehr Informationen konsultieren Sie eine Formelsammlung wie z.B. den Abschnitt Trigonometrische Funktionen skTop Mathematik oder den Abschnitt Trigonometrie von mathematik.net. Weite von Tange Cotang Weitere Winkelfunktionen rken am Ende dieses Abschnitts an, dass bisweilen auch andere Winkelfunktionen, die sich aus den bisherigen ableiten, det werden. Es handelt sich dabei in allen Fällen lediglich um Abkürzungen, die für gewisse Zwecke praktisch sind. So or allem in der englischsprachigen Literatur der Secans und der Cosecans gebräuchlich. Sie sind definiert durch 1/cos und csc = 1/sin . In verschiedenen Spezialgebieten der Mathematik wird man über weitere Winkelfunktionen, m Beispiel den Semiversus, definiert als sem = sin2(/2), stolpern. Die älteste Winkelfunktion wurde im zweiten stlichen Jahrhundert von Hipparchos von Nicäa tabelliert: die Sehnenfunktion, die in der modernen Form als = 2 sin(/2) geschrieben wird. Spezielle Winkel Zum Seiten nche Winkel lassen sich die Winkelfunktionen durch die uns bisher bekannten Rechenoperationen, insbesondere durch twurzeln, darstellen. In der folgenden Tabelle sind einige dieser Winkel und die zugehörigen Funktionswerte aufgelistet: sin 0° cos 0 1 1 1 2 2 __ 2 1 30° 1 45° 2 1 60° tan __ 3 1 cot 0 ± __ 3 __ 3 3 __ 2 1 1 2 __ 3 2 1 __ 3 2 1 __ 3 3 90° 1 0 ± 0 180° 0 1 0 ± 270° 1 0 ± 0 Brüchen, die Quadratwurzeln enthalten, sind die Nenner rational gemacht. Das Symbol ± nde Wert nicht definiert ist. Das Bogenmaß deutet an, dass der Zum Seiten Spezielle W Es gibt verschiedene Winkelmaße, d.h. Systeme, um die Größe eines Winkels anzugeben. Die Ihnen wahrscheinlich vertrauteste Methode ist das Gradmaß, das auf der Einteilung des vollen Kreises in 360 "Winkelgrade" (und der feineren Einteilung des Grades in 60 Winkelminuten und der Minute in 60 Winkelsekunden) beruht. Wieso der volle Winkel ausgerechnet 360 Grad misst, hat historische Gründe und ist vom mathematischen Standpunkt aus gesehen gar nicht so vorteilhaft. Für viele Zwecke günstiger ist ein anderes System, das sogenannte Bogenmaß. In ihm wird die Größe eines Winkels durch die Länge des entsprechenden Bogens am Einheitskreis gemessen. Das ist in der nebenstehenden Skizze dargestellt: Anstatt den Winkel in Grad anzugeben, dient die Länge des hellblauen Bogenstücks als Maß für seine Größe. Der volle Winkel ist im Bogenmaß durch den Umfang des Einheitskreises gegeben, d.h. durch 2. Beispiel: Ein Winkel von 60° (also ein Sechstel des vollen Winkels) ist im Bogenmaß /3, das ist ungefähr 1.0472. Hier sehen wir einen der Nachteile des Bogenmaßes: "Runde" Winkel wie 30°, 45°, 60°, 90°, 180° oder 360° werden durch irrationale Zahlen dargestellt. Sie werden am besten als rationale Vielfache ngeschrieben (wie /3 für 60°). inkelangabe im Bogenmaß geschieht meist ohne Angabe einer "Einheit" (d.h. ohne ein Symbol wie °). Manchmal wird die "Radiant" (abgekürzt rad) herangezogen und wie eine Einheit verwendet (z.B.: 60° ist /3 rad, also ungefähr rad), aber das ist nicht unbedingt notwendig. Weiters wird gelegentlich für die Umrechnung eines Winkels in das maß die Bezeichnung arc (lateinisch: arcus = der Bogen) verwendet, z.B. arc(60°) = /3. rechnung zwischen Grad- und Bogenmaß ist eine einfache Sache: Ist ein im Gradmaß gegebener Winkel, so ist sein Bogenmaß 2 × /360°. Umgekehrt muss ein Wert im Bogenmaß 360°/(2) mit multipliziert werden, um den chenden Winkel im Gradmaß zu bekommen. zeichnungsweise: Wir haben Winkeln bisher mit griechischen Buchstaben bezeichnet. Das wird oft auch beibehalten, as Bogenmaß verwendet wird. Die Angabe = 60° bedeutet dann dasselbe wie = /3. Also Achtung: Die Verwendung genmaßes wird in dieser Konvention nur daran erkannt, dass das Grad-Symbol ° fehlt! Da die Größe eines Winkels im maß durch eine (Bogen-)Länge dargestellt wird, sind auch andere Buchstaben gebräuchlich (wie z.B. x, der typische abe für eine Variable). genmaß eines Winkels kann auch anhand eines Kreises mit beliebigem Radius r ermittelt werden. e in der nebenstehenden Skizze, der zugehörige Kreisbogen die Länge s, so ist der Winkel im maß durch den Quotienten s/r gegeben. Für den Einheitskreis (r = 1) reduziert sich das auf die efinition. Der Grund für diese Eigenschaft besteht darin, dass alle "Tortenecken" mit demselben zueinander ähnlich sind. Sie unterscheiden sich lediglich in ihrer Größe, sind also jeweils lasene" oder "geschrumpfte" Versionen voneinander. Daher ist das Längenverhältnis s/r für all iguren gleich, kann also als Maß für den Winkel dienen. nden wir uns wieder den Winkelfunktionen zu. Einige unserer bisherigen Formeln haben sich auf das Gradmaß bezogen nnen ins Bogenmaß umgeschrieben werden. So wird die Periodizität (6) von Sinus und Cosinus im Bogenmaß durch sin( + 2) = sin cos( + 2) = cos . rückt, und die Beziehungen (8)(11) übersetzen sich zu (6b) sin(/2 ) = cos (8b) cos(/2 ) = sin sin( + /2) = cos cos( + /2) = sin sin( ) = sin (9b) (10b) cos( ) = cos sin( + ) = sin (11b) cos( + ) = cos . e für Tangens und Cotangens angegebenen Beziehungen sowie die obige Tabelle mit Werten der Winkelfunktionen für e Winkel können ins Bogenmaß übersetzt werden (siehe den nebenstehenden Button). enmaß sind der Sinus und der Tangens für kleine Winkel ungefähr gleich dem Winkel selbst: sin und tan , (22) | 1 ist. Ist im Gradmaß gegeben, so müssen diese Formeln zu sin tan 2 × /360° abgeändert werden. e Taschenrechner und Computerprogramme unterstützen beide Winkelmaße; andere wiederum benutzen nur das (in der n Mathematik als natürlicher geltende) Bogenmaß. Das sollte bei der Verwendung elektronischer Rechenhilfen immer t werden mehr dazu weiter unten. Die inversen Winkelfunktionen mal kennt man den Wert einer Winkelfunktion für einen bestimmten Winkel und möchte gern den Winkel selbst kennen. spielsweise jener Winkel (zwischen 0° und 90°), für den sin = 0.2 ist. Wie groß ist ? Da diese Problemstellung über bisher bekannten Rechenoperationen hinaus weist, geben wir dem Resultat einen Namen wir nennen es Arcus Sinus, rzt asin und überlassen die Berechnung Werkzeugen, die das für uns tun. Der Name leitet sich vom Bogenmaß her: t ist der Winkel ( = Bogen = arcus). asin(0.2) ist also jener Winkel, dessen Sinus 0.2 ist. Alle wissenschaftlichen nrechner und viele Rechenprogramme am Computer liefern uns das Resultat auf Knopfdruck: Der gesuchte Winkel ist ngsweise (im Gradmaß) 11.537° bzw. (im Bogenmaß) 0.2014. Sinus ist die zum Sinus "inverse Funktion" (oder "Umkehrfunktion"). Der Grund für diese Benennung ist einfach zu en: "Invertieren" heißt, salopp gesagt, "umkehren" oder "umdrehen". Die Sinusfunktion ordnet jedem Winkel seinen Sinus die Arcus-Sinus-Funktion macht das Umgekehrte: sie ordnet jedem Sinuswert den Winkel zu, ganz ähnlich, wie das ziehen die zum Quadrieren inverse Funktion ist. Allerdings müssen wir bei einer mathematisch genauen Definition der Sinus-Definition eines berücksichtigen: es gibt zwei Winkel, deren Sinus 0.2 ist, nämlich 11.537° und 168.463° (das sind mentärwinkel; ihre Summe ist 180°). Erinnern wir uns an Formel (10) sie besagt, dass Winkel, deren Summe 180° ist, ben Sinus haben. Wenn wir die Sinusfunktion invertieren wollen, müssen wir also festlegen, welcher dieser beiden n unter asin(0.2) verstanden werden soll. (Der andere kann dann als Supplementärwinkel daraus gewonnen werden). as kann in Analogie zum Wurzelziehen als Umkehrung des Quadrierens verstanden werden: es gibt zwei Zahlen, deren t 4 ist (nämlich 2 und 2), und nur eine davon (nämlich die positive) wird als "Wurzel aus 4" bezeichnet. (Die andere kann s die dazu Negative gewonnen werden). naue Definition des Arcus Sinus lautet: Sei 1 x 1. Dann ist asin x jener Winkel , für den sin = x ist, und der Zum Seiten en 90° und 90° (im Bogenmaß: zwischen /2 und /2) liegt. chten ist, dass die Funktion asin nicht für jede reelle Zahl definiert ist: Da etwa die Zahl 2 nicht der Sinus eines Winkels nn vergleiche (3) , existiert asin(2) ebenso wenig wie die Wurzel aus 4. Wenn Sie einem Rechner dennoch eine Anweisung geben, wird er entweder mit einer Fehlermeldung reagieren oder eine komplexe Zahl ausgeben. (Im Rahmen mplexen Zahlen kann ein Quadrat negativ und ein Sinus größer als 1 sein, aber das braucht uns im Moment nicht zu rn). nalog kann mit den anderen Winkelfunktionen verfahren werden. Hier eine Tabelle der wichtigsten inversen funktionen (auch Arcus-Funktionen genannt) und der zugehörigen Winkelbereiche: Funktion Inverse liefert einen Winkel von im Bereich Name andere Bezeichnung asin Arcus Sinus sin 90° 90° arcsin, sin1, inv sin acos Arcus Cosinus cos 0° 180° arccos, cos1, inv cos atan Arcus Tangens tan 90° 90° arctan, tan1, inv tan acot Arcus Cotangens cot 90° 90° 0° arccot, cot1, inv cot d acos sind für alle reellen Zahlen zwischen 1 und 1, atan und acot für alle reelle Zahlen ohne Einschränkung definiert. ch zu den in der Tabelle angegebenen Bezeichnungen sind auch noch manchmal Varianten wie arctg, ctg 1, inv tg und e zu finden. Die Bezeichnungen mit "inv" sind auf Taschenrechnern oft mit Hilfe von Zweitfunktionstasten realisiert. Die e des berechneten Winkels kann meist wahlweise im Gradmaß oder im Bogenmaß erfolgen. (Weiter unten werden wir Tipps zur Verwendung von Taschenrechner und Computer geben). Ebene Polarkoordinaten Zum Seiten en in einem früheren Kapitel bereits von den (ebenen) oordinaten gesprochen. Ihr Sinn besteht darin, die Lage eines Punktes r Zeichenebene, wie in der nebenstehenden Skizze angedeutet, durch Polarkoord seinen Abstand r vom Ursprung und den Winkel , den die Strecke zwischen Ursprung und P mit der (positiven) x-Achse einschließt (er wird auch Polarwinkel genannt) akterisieren. Dabei wird wie in den oben verwendeten iagrammen im Gegenuhrzeigersinn gemessen. Meistens werden seine m Bereich von 0° bis 360° (bzw. im Bogenmaß von 0 bis 2 ) angegeben. mal ist es bequemer, statt dessen die Werte zwischen 180° und 180° (im Bogenmaß zwischen und ) zuzulassen. nd unseres bisherigen Wissens über Winkelfunktionen sind wir nun in der Lage, den quantitativen Zusammenhang dieser aten mit den kartesischen (rechtwinkeligen) Koordinaten anzugeben. obigen Skizze geht unmittelbar hervor, dass x = r cos (23) y = r sin (24) mit können die kartesischen aus den Polarkoordinaten eines Punktes P berechnet werden. Sind umgekehrt die chen Koordinaten (x, y) eines Punktes bekannt, so können seine Polarkoordinaten (r, ) aus den Gleichungen r 2 = x2 + y 2 tan = (25) y (26) x t werden: r folgt durch Wurzelziehen aus der ersten Gleichung. Liegt P im ersten oder vierten Quadranten (d.h. ist x > 0), durch atan(y/x) gegeben, ansonsten ist noch 180° (im Bogenmaß ) hinzuzufügen (oder abzuziehen, was auf dasselbe äuft). wir r = 1 in den Beziehungen (23)(24), so ergibt sich eine einfache Deutung der oben verwendeten Zeigerdiagramme: nd sin sind die (kartesischen) Koordinaten x und y des Zeiger-Endpunktes am Einheitskreis. Der Winkel hat ie Bedeutung des Polarwinkels . ordinaten werden in vielen (insbesondere physikalischen) Anwendungen der Mathematik verwendet und spielen eine e Rolle in der Theorie der komplexen Zahlen. Winkelfunktionen am Computer wissenschaftliche Rechner" und zahlreiche Computerprogramme können mit Winkelfunktionen umgehen. Bei all diesen ugen sollten Sie auf einige Dinge achten: Wie wir oben schon gesehen haben, gibt es gibt verschiedene Systeme zur Angabe von Winkeln. Falls das Werkzeug Ihrer Wahl ein "Umschalten" zwischen diesen Winkelmaßen erlaubt, vergewissern Sie sich, dass tatsächlich das von Ihnen gewünschte eingestellt ist. Ansonsten kann es Ihnen passieren, dass Sie sin(31°) berechnen wollen und statt dessen sin(31 rad) erhalten, vielleicht ohne es zu merken. Typische Tastenbezeichnungen auf Taschenrechnern sind: o Gradmaß (auch Altgrad genannt): DEG o Bogenmaß: RAD o Neugrad-System (rechter Winkel = 100 Neugrad 100g 100 gon, 1g = 100 Neuminuten 100c, 1c = 100 Neusekunden 100cc): GRD wobei letzteres hauptsächlich im Vermessungswesen verwendet wird (1 Neugrad wird auch als 1 gon bezeichnet). Manche Werkzeuge arbeiten nur im Bogenmaß, da es in der Mathematik als das natürlichere gilt. In diesen Fällen müssen Sie etwa sin(31°) als sin(31*/180) berechnen. Die inversen Winkelfunktionen (Arcus-Funktionen) sind nicht einheitlich bezeichnet. Siehe dazu die oben angegebene Tabelle. Auf Taschenrechnern sind sie oft mit Hilfe der Zweitfunktionstaste INV, manchmal auch ARC, realisiert. Da der Rückgabewert einer Arcus-Funktion ein Winkel ist, sollten Sie auch hier beachten, dass es verschiedene Winkelmaße gibt. Beispielsweise ist asin(1) im Gradmaß 90° und im Bogenmaß /2, also ungefähr 1.5707963. merische Berechnungen können Sie beispielsweise eines der beiden Werkzeuge mathe online Mini-Rechner oder lc benutzen. Beide beruhen auf JavaScript und verwenden das Bogenmaß. Um eine Rechnung wie sin(19.5°) × 3.7 uführen, geben Sie sin(19.5*PI/180)*3.7 ein. Um asin(0.5) im Gradmaß zu berechnen, geben Komplexe Zum Seiten in(0.5)*180/PI ein. Die obigen Rechner für Sinus/Cosinus und Tangens/Cotangens sind hingegen eigens für das aß programmiert und benötigen keine derartige Umrechnung. auch Programme, die symbolische (exakte) Berechnungen durchführen können. Ein solches, auf dem Computer-AlgebraMathematica beruhendes Werkzeug ist athServ Project der Vanderbilt University. Es eignet sich insbesondere dazu, die Werte von Winkel- und Arcus-Funktionen rc" geschrieben) für spezielle Winkel zu berechnen. Falls eine Darstellung durch einfache Rechenoperationen wie twurzeln existiert, wird sie angezeigt. Das Werkzeug arbeitet im Bogenmaß. Für sin(60°) geben Sie sin(pi/3) ein. Ist öße als Dezimalzahl angegeben, so wird die Berechnung numerisch ausgeführt. Sehen Sie sich den Unterschied der te für die Eingaben arcsin(-1/2) und arcsin(-0.5) an! In gewissem Umfang werden darüber hinaus auch Ausdrücke vereinfacht. Beispiel: Geben Sie 2 sin(x)cos(x) ein! (Achtung: Schreiben Sie Potenzen von unktionen in der Form (sin(x))^2 oder sin[x]^2 hier scheint ein kleiner Programmierfehler zu verhindern, in(x)^2 richtig gelesen wird). Ausblicke Zum Seiten inkelfunktionen (und ihre Inversen) lässt sich noch viel sagen, und sie werden uns beim Fortschreiten des Stoffs noch oft en. Sie sind unentbehrlich bei der Lösung vieler geometrischer Probleme, in denen Dreiecke eine Rolle spielen. Das mathematische Teilgebiet, das sich mit der Rolle der Winkelfunktionen in Dreiecken (und ganz allgemein bei der Lösung von Vermessungsproblemen) beschäftigt, heißt Trigonometrie. Winkelfunktionen sind, wie der Name sagt, Funktionen. (Sie fallen in die Klasse der sogenannten "transzendenten Funktionen"). Von großer Bedeutung ist ihre Darstellung in Form von Funktionsgraphen, die einem späteren Kapitel vorbehalten bleibt. Andere Kapitel behandeln Ableitungen und Integrale der Winkelfunktionen sowie ihre hervorragende Rolle bei der Lösung von Differentialgleichungen. Methoden zu ihrer numerischen Berechnung ergeben sich, wenn Potenzreihen betrachtet werden. Schließlich sind treten Winkelfunktionen in der Theorie der komplexen Zahlen und in Form der sogenannten Fourierreihen bei der Analyse periodischer Funktionen auf. en in diesem Kapitel viele grundsätzliche Tatsachen über Winkelfunktionen zusammengestellt. Konsultieren Sie es auch wenn Sie Eigenschaften dieser Funktionen zum Lösen von Problemen und zum Weitergehen im Stoff benötigen! Die in diesem Kapitel empfohlenen WebRessourcen: mit Mathematica, ein Angebot des MathServ Project. Empfehlenswerte Formelsammlungen zum Thema sind der Abschnitt Trigonometrische Funktionen von DeskTop Weitere Angebote von mathe online zum Thema: Zum Kapitel Winkelfunktionen der Galerie Applet Die Graphen von sin, cos und tan mathe online Mini-Rechner, JavaCalc Unter der Kategorie Mathematische Einzelthemen > Winkelfunktionen und Trigonom Funktion Differenzie Integrie Differentialgle (in Vorbere Potenzre (in Vorbere Komplexe Fourierre (in Vorbere Mathematik und der Abschnitt Trigonometrie von mathematik.net. Trigonometrie unserer Ressourcensammlung Mathe-Links und Online-Werkzeuge finden Sie Links zu weiteren Lernhilfen. Siehe auch die interaktiven Tests zum Thema. Zum Seitenanfang Zum Lexikon Zur Galerie Zum Kapitel Winkelfunktionen der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page