2.4

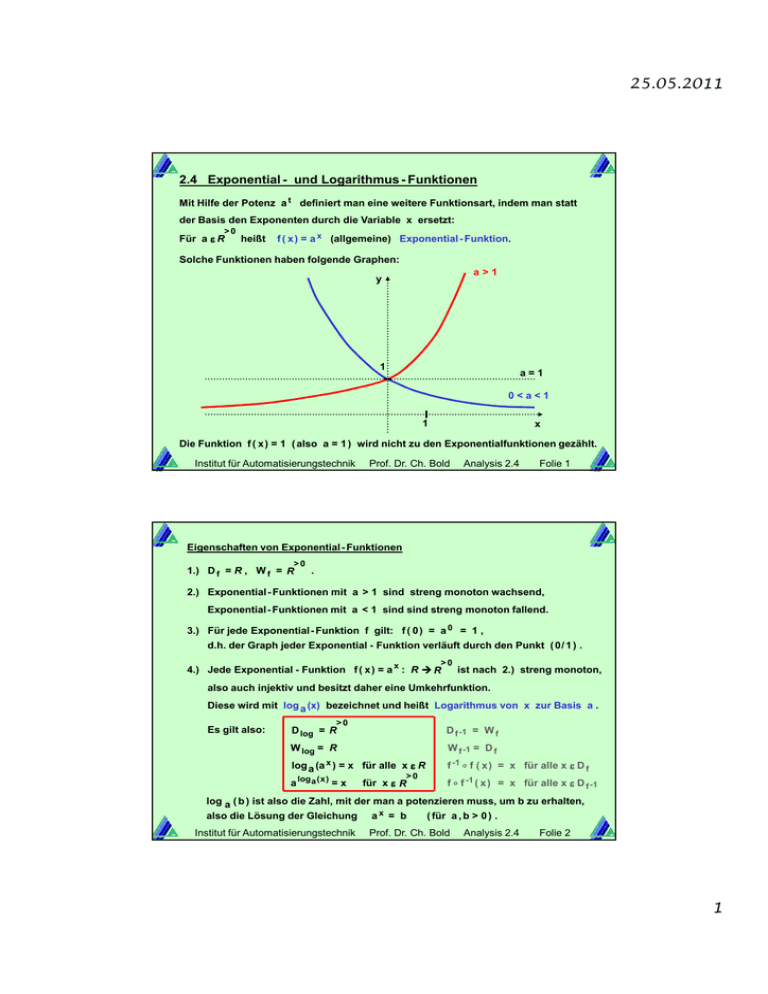
25.05.2011
2.4 Exponential - und Logarithmus - Funktionen
Mit Hilfe der Potenz a t definiert man eine weitere Funktionsart, indem man statt
der Basis den Exponenten durch die Variable x ersetzt:
>0
Für a ε R
heißt
f ( x ) = a x (allgemeine) Exponential - Funktion.
Solche Funktionen haben folgende Graphen:
a>1
y
1
a=1
0<a<1
1
x
Die Funktion f ( x ) = 1 ( also a = 1 ) wird nicht zu den Exponentialfunktionen gezählt.
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 1
Eigenschaften von Exponential - Funktionen
>0
1.) D f = R , W f = R
.
2.) Exponential - Funktionen mit a > 1 sind streng monoton wachsend,
Exponential- Funktionen mit a < 1 sind sind streng monoton fallend.
3.) Für jede Exponential- Funktion f gilt: f ( 0 ) = a 0 = 1 ,
d.h. der Graph jeder Exponential - Funktion verläuft durch den Punkt ( 0/ 1 ) .
>0
4.) Jede Exponential - Funktion f ( x ) y= a x : R R
a>1
ist nach 2.) streng monoton,
also auch injektiv und besitzt daher eine Umkehrfunktion.
Diese wird mit log a (x) bezeichnet und heißt Logarithmus von x zur Basis a .
Es gilt also:
>0
D log = R
D f -1 = W f
W log = R
W f -1 = D f
1
log a (a x ) = x für alle x ε R
f -1 o f ( x ) = x für alle x ε D f
a log a (x) = x
f o f -1 ( x ) = 0x < für
a < alle
1 x ε D f -1
>0
für x ε R
log a ( b ) ist also die Zahl, mit der man a potenzieren muss, um b zu erhalten,
1( für a , b > 0 ) .
x
also die Lösung der Gleichung a x = b
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 2
1
25.05.2011
Graphen der Logarithmus - Funktionen
y
Die Graphen der Logarithmus -
y=x
Funktionen erhält man aus
den Graphen der Exponential Funktionen durch Spiegelung an
der ersten Winkelhalbierenden.
a x für 0 < a < 1
1
log a (x) mit a > 1
a x für a > 1
Der Graph jeder Logarithmus -
x
1
Funktion verläuft also durch
den Punkt ( 1/ 0 ) , d.h. alle
Logarithmus- Funktionen
haben an der Stelle x 0 = 1
log a (x) mit 0 < a < 1
eine Nullstelle.
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 3
Rechenregeln für Logarithmen
Für x > 0 und y > 0 gilt:
1.) log a ( x . y ) = log a ( x ) + log a ( y )
x
2.) log a ( y ) = log a ( x ) - log a ( y )
Achtung:
3.) log a ( x t )
log a ( x + y ) und log a ( x - y ) !
=
Keine Rechenregeln gibt es für
t . log a ( x )
Bemerkung
>0
Wegen D log = R
Daher gilt z.B.
gelten diese Regeln also nur für x > 0 und y > 0 .
log a ( x 2 ) = 2 . log a ( x )
3.)
nicht für alle reellen Zahlen x , sondern
nur für x > 0.
log a ( x 2 ) = log a ( | x | 2 ) = 2 . log a ( | x | ) .
Eine allgemeingültige Umformung ist
Beweis zu 1.):
log a ( x . y ) = log a ( x ) + log a ( y )
a
log a ( x . y )
= x.y
( )
a ...
log a ( x ) + log a ( y )
=
a
= a
Institut für Automatisierungstechnik
log a ( x )
.a
log a ( y )
Prof. Dr. Ch. Bold
= x.y
Analysis 2.4
Folie 4
2
25.05.2011
Satz 5
( Basiswechsel bei Logarithmen )
Für alle reellen Zahlen a, b und x
mit a, b, x > 0 und a
Beweis :
1, b
Es gilt
log b ( x ) =
1 gilt:
log b ( x )
x
=
b
log a ( x )
=
log a ( b
log a ( x )
=
log b ( x ) . log a ( b )
=
log b ( x )
log a ( x )
log a ( b )
log a ( x )
log a ( b )
log a ( ... )
log b ( x )
)
: log a ( b )
0 , da b
1
Bemerkung
Wenn man also die Logarithmen zu einer Basis kennt ( hier a ) , kann man die
Logarithmen zu jeder anderen Basis ( hier b ) daraus berechnen.
Für Taschenrechner würde also z.B. eine Logarithmus - Funktion ausreichen.
Meist gibt es trotzdem zwei, weil die beiden folgenden besonders wichtig sind:
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 5
Zehner - Logarithmus
•
Basis a = 10
Der Logarithmus zur Basis 10 heißt dekadischer Logarithmus oder
Zehner - Logarithmus und wird mit lg bezeichnet:
lg ( x ) = log 10 ( x )
Der Vorteil des dekadischen Logarithmus ist seine Beziehung zum
dekadischen Zahlsystem.
So weiß man wegen der Monotonie der Logarithmus - Funktionen auch ohne
Taschenrechner, was vor dem Komma eines Zehner - Logarithmus steht.
Beispiel:
lg ( 3245 )
= 3, ...
lg ( 1000 )
= 3
Die Zahl vor dem Komma
des Logarithmuswertes
ist also um 1 kleiner als
lg ( 10000 ) = 4
die Anzahl der Stellen
1000 < 3245 < 10000
Institut für Automatisierungstechnik
der Ausgangszahl.
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 6
3
25.05.2011
Natürlicher Logarithmus
•
Basis a = e = 2,718281828459 ...
Die Zahl e heißt Euler‘ sche Zahl.
Sie ist wie
π irrational.
Der Logarithmus zur Basis e heißt natürlicher Logarithmus oder
Logarithmus naturalis und wird mit ln bezeichnet:
ln ( x ) = log e ( x )
Der Vorteil des natürlichen Logarithmus wird erst bei der Differential - und
Integralrechnung verständlich.
Er ist allerdings so gravierend, dass man in der Mathematik fast ausschließlich
den natürlichen Logarithmus benutzt.
Institut für Automatisierungstechnik
Satz 6
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 7
( Basiswechsel bei Exponentialfunktionen)
Ebenso wie bei Logarithmen kann man auch jede Exponentialfunktion auf eine
beliebige andere Basis umformen.
Umformung auf die wichtigste Basis e :
a
x
=
(e ln ( a ) ) x
= e
x . ln(a)
, also
a
x
= e
x . ln(a)
f ( x ) = e x heißt spezielle Exponential - Funktion oder kurz die Exponential Funktion oder noch kürzer e - Funktion.
Bei umfangreichen Exponenten schreibt man auch exp ( x ) statt e x .
Entsprechend heißt die Funktion
f ( x ) = ln ( x ) der Logarithmus.
Zusammenfassung der Rechenregeln für ln ( x ) :
Die Regeln 1 bis 4 gelten für nur für x , y > 0 ,
Regel 5 gilt für alle reellen Zahlen x .
1.) ln ( x . y ) = ln ( x ) + ln ( y )
x
2.) ln ( y ) = ln ( x ) - ln ( y )
3.) ln ( x t ) = t . ln ( x )
4.) e ln (x )
= x
5.) ln ( e x ) = x
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 8
4
25.05.2011
Graphen von e x und ln ( x )
y
y=x
ex
ln ( x )
1
x
1
Institut für Automatisierungstechnik
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 9
Exponentielles Wachstum
Exponential - Funktionen haben die Eigenschaft, dass sich der Funktionswert in
gleichbleibenden Abständen verdoppelt.
Ein derartiges Wachstum ist intuitiv nur sehr schwer zu erfassen, z.B.
•
Seerosenteich
•
Reiskörner auf ein Schachbrett legen
2. Zeile: 9h 6m 8s
Anzahl Reiskörner:
2 64 - 1 = 18 446 744 073 709 551 615
Alle Reiskörner füllen einen Güterzug,
3. Zeile: 97T 9h 6m 8s
4. Zeile: 68 Jahre
der 500 mal um die Erde herumreicht !
5. Zeile: 17408 Jahre
Wie lange würde der Rechner
benötigen, um die restlichen
Reiskörner zu zeichnen ?
6. Zeile: 4,4 Mio. Jahre
1. Zeile dauerte 2 min 8 sec.
Institut für Automatisierungstechnik
7. Zeile: 1,1 Mrd. Jahre
8. Zeile: 300 Mrd. Jahre
Prof. Dr. Ch. Bold
Analysis 2.4
Folie 10
5