1. a. Die bewegten Ladungen unterliegen der Lorentz
Werbung
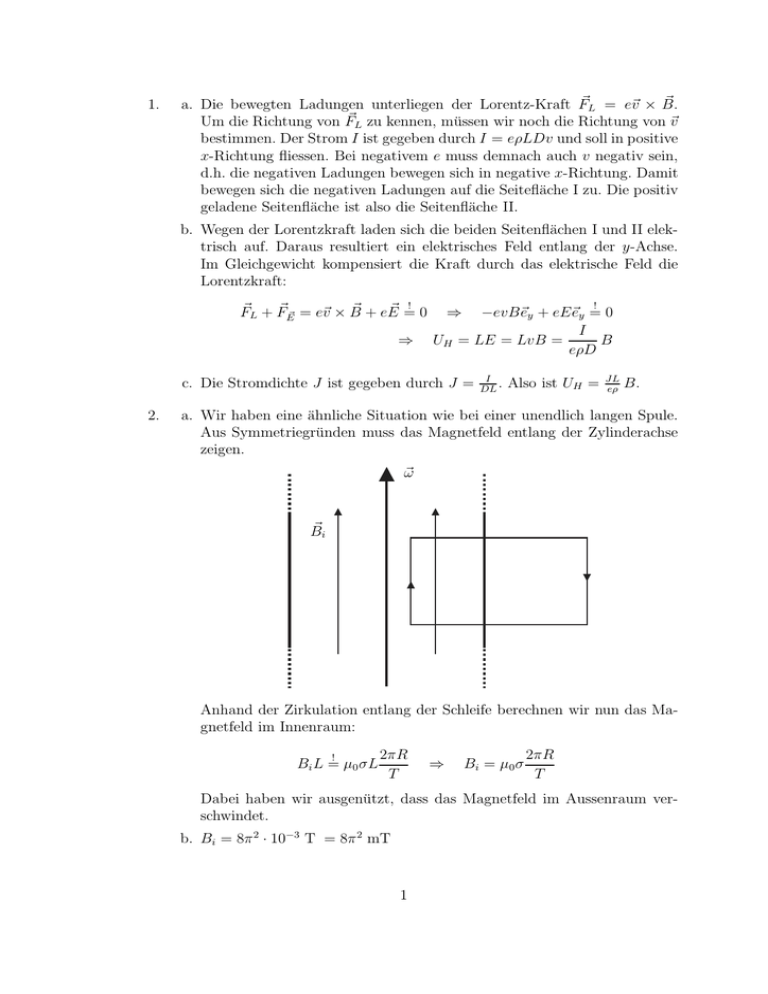
1. ~ a. Die bewegten Ladungen unterliegen der Lorentz-Kraft F~L = e~v × B. Um die Richtung von F~L zu kennen, müssen wir noch die Richtung von ~v bestimmen. Der Strom I ist gegeben durch I = eρLDv und soll in positive x-Richtung fliessen. Bei negativem e muss demnach auch v negativ sein, d.h. die negativen Ladungen bewegen sich in negative x-Richtung. Damit bewegen sich die negativen Ladungen auf die Seitefläche I zu. Die positiv geladene Seitenfläche ist also die Seitenfläche II. b. Wegen der Lorentzkraft laden sich die beiden Seitenflächen I und II elektrisch auf. Daraus resultiert ein elektrisches Feld entlang der y-Achse. Im Gleichgewicht kompensiert die Kraft durch das elektrische Feld die Lorentzkraft: ~ + eE ~ =! 0 F~L + F~E~ = e~v × B ⇒ ! ⇒ −evB~ey + eE~ey = 0 I UH = LE = LvB = B eρD c. Die Stromdichte J ist gegeben durch J = 2. I . DL Also ist UH = JL eρ B. a. Wir haben eine ähnliche Situation wie bei einer unendlich langen Spule. Aus Symmetriegründen muss das Magnetfeld entlang der Zylinderachse zeigen. ~ω ~i B Anhand der Zirkulation entlang der Schleife berechnen wir nun das Magnetfeld im Innenraum: ! Bi L = µ0 σL 2πR T ⇒ Bi = µ0 σ 2πR T Dabei haben wir ausgenützt, dass das Magnetfeld im Aussenraum verschwindet. b. Bi = 8π 2 · 10−3 T = 8π 2 mT 1 3. ~ · ~e kennen wir aus den Übungen: a. Den Mittelwert von S D E ~ · ~e S = t ε0 c2 ~ 2 ~ · E · k · ~e 2ω Die Beträge der ~k-Vektoren in den beiden Medien sind gegeben durch ω ω n und kp = p c c kn = Das Verhältnis der Amplituden der elektrischen Felder in den beiden Medien erhalten wir aus den Fresnel-Formeln: Ep 2kn 2n = = En kn + kp n+p Also: D T =D ~p · ~e S E Et ~n · ~e S = t p 4x 4n2 · = 2 (n + p) n (1 + x)2 mit x = n p b. Wir schauen, ob die Bedingung T ≤ 1 eine Einschränkung für x bedeutet: 4x ≤1 (1 + x)2 ⇔ 4x ≤ (x + 1)2 = x2 + 2x + 1 0 ≤ x2 − 2x + 1 = (x − 1)2 ⇔ Diese Bedingung ist für alle x erfüllt. c. Um das x, das zu T = 1 führt, zu finden, ersetzen wir oben ≤ durch = und erhalten x = ±1. Nach Voraussetzung ist x positiv, also x = 1. Alternative Rechnung zu b. und c.: T (x) ist eine stetig differenzierbare Funktion mit T (0) = 0 und limx→∞ T (x) = 0. Dazwischen nimmt die Funktion ein Maximum an. Dieses Maximum erhalten wir aus T ′ (x) = 0. Die Rechnung führt wieder auf x = 1. An dieser Stelle ist T = 1. Damit sind die Teilfragen b. und c. beantwortet. 4. Am Ort ~r haben wir die Superposition der Kugelwellen, die von den beiden Punktquellen ausgehen: ψtotal (~r) ∝ ~ eikr eik|~r−d| + r ~ r − d~ Wir verwenden jetzt die Taylor-Entwicklung für ~r − d~: ~ r − d~ ~r · d~ ≈ r 1 − 2 |~r| 2 und erhalten: ik |~ r −d~| e Mit der Approximation ~ ikr 1− ~r·d2 ≈e 1 |~r−d~| ≈ 1 |~ r| |~ r| = eikr e−ikd cos ϕ haben wir schliesslich: eikr eikr −ikd cos ϕ eikr 1 + e−ikd cos ϕ + ·e = r r r ikd cos ϕ −ikd cos ϕ 2 (1 + cos(kd cos ϕ)) · 1+e ∝ 1+e ψtot (~r) ∝ |ψtot (~r)|2 Die Bedingung für destruktive Interferenz ist also kd cos ϕ = (2n + 1)π, wobei n eine ganze Zahl bezeichnet. 3











