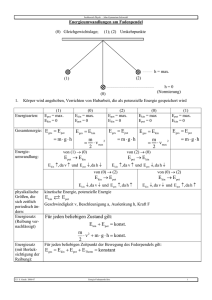
und P - IAP TU

Kapitel 4
Energie und Arbeit
Kraftfelder
► Wenn wir jedem Punkt des Raums eindeutig einen
  Kraft-Vektor
zuordnen können, erhalten wir ein Kraftfeld F (r )
 
Häufig tauchen in der Physik Zentral-Kraftfelder auf : F (r )  f (r ) rˆ
 Die Kraft zeigt immer auf ein festes Zentrum
 Stärke der Kraft hängt (nur) von r ab.
 f(r) < 0 : Kraft ist attraktiv (z.B. Gravitation)
 f(r) > 0 : Kraft ist repulsiv (z.B. zwischen gleichen elektrischen Ladungen)
2
Beispiel Zentralfeld

r
Attraktives Kraftfeld der Gravitation einer Vollkugel (rot markiert) : Äquipotentialflächen def.
Bereiche gleichen Potentials (bzw. in diesem Fall auch gleicher Kraft). Die Äquipotentialflächen
sind konzentrische Kreise. Die attraktive Kraft F ist senkrecht zu den Potentialflächen, in
Richtung (–r) gerichtet.
3
Beispiel für ein Nicht-Zentralfeld
 

F  FE  FM
 M E rˆE M M rˆM 
 Gm 2 

2
r
r
M
 E

  rˆ
Gravitationsfeld zweier Massen: z.B. Kraft auf eine Probemasse m zwischen Erde und Mond. Da
beide Einzelfelder von Erde und Mond attraktive Zentralfelder sind, wird es irgendwo zwischen
Erde und Mond einen Bereich geben, wo sich die Gravitationskräfte der beiden Himmelskörper
gerade aufheben („Trennkurve“). Auch außerhalb dieses Bereiches sind die Gravitationsfelder
von Erde und Mond modifiziert im Vergleich zum Feld einer einzelnen Masse. Das gesamte
Kraftfeld kann als Überlagerung der Einzelfelder geschrieben werden.
4
Homogene und inhomogene Kraftfelder
► Ein Kraftfeld heißt homogen (innerhalb eines Raumbereichs), wenn
Richtung und Betrag einer Kraft nicht vom Ort abhängen, andernfalls ist das
Kraftfeld inhomogen.
Das Feld tief im Inneren (z << L)
eines Plattenkondensators kann als
homogen angenommen werden. Am
Rand entstehen inhomogene Felder
h
Auch das Gravitationsfeld kann in der Nähe der
Erdoberfläche (h << R) als homogen angenommen
werden, d.h. Kraft und Beschleunigung variieren nur
vernachlässigbar wenig mit der Höhe.
5
Bewegung in Kraftfeldern : Arbeit
F||
P

r
F┴

r t  t 
Arbeit
= Kraft Weg
Wir betrachten die Bahnkurve eines
Teilchens in einem Kraftfeld : An
einem beliebigen Punkt P wirkt eine
Kraft. Wir können die Kraft zerlegen
in Komponenten F┴ und F|| , d.h.
senkrecht und parallel zur Tangente
an die Bahn in P
F|| ist parallel zur Bahn, d.h. parallel zur
Geschwindigkeit v  F|| bewirkt eine
Beschleunigung, d.h. Veränderung des
Betrages der Geschwindigkeit v;
F┴ ist senkrecht zur Bahn, d.h. senkrecht
zur Geschwindigkeit v  F ┴ bewirkt eine
Krümmung der Bahn, d.h. lediglich
Veränderung
der
Richtung
der
Geschwindigkeit v
6
Allg. Definition der Arbeit längs eines
Weges von P1 nach P2 auf der Bahn :
Definition der Leistung
Einheiten :
P  W
[Arbeit] = Nm = Joule
W12  
P2
P1
  
F (r ) dr
d.h. Arbeit pro Zeit
[Leistung] = Joule/s = Watt
7
Arbeit bei einfacher Bewegung im Schwerfeld
P2
h
P1
Bahn gegeben durch x = x(y) von y1 = 0 bis y2 = h
 
Kraft in Punkt (x,y) : F  FG  mg eˆ y
P2
y2
h
 

 W12  F dr   mg eˆ y dr   mg dy   mg dy  mgh




P2
P1
P1
y1
0
8
Konservative/nicht-konservative Kraftfelder
Wenn die Arbeit in einem Kraftfeld
unabhängig vom Weg ist, gilt :
W
  
 F (r ) dr  0
P1  P2  P1
 Das Kraftfeld heißt dann konservativ
Wenn die Arbeit in einem Kraftfeld
abhängig vom Weg ist, gilt i.d.R. :
W
  
 F (r ) dr  0
P1  P2  P1
 Das Kraftfeld heißt dann nicht-konservativ
Anmerkung : Nur wenn das Kraftfeld konservativ ist, kann die potentielle
Energie (d.h. Energie abhängig von Position) sinnvoll definiert werden
(andernfalls würde die Energie vom vorherigen Weg zur aktuellen Position abhängen)
9
Beispiel für konservative Kraftfelder

F  (0,0, F )
Arbeit in einem homogenen Kraftfeld :
Überlegungen (ohne Rechnung) : Homogenes Feld
 Kraft überall konstant. Betrachte 2 mögliche
Wege I,II zwischen P1 und P2: Senkrecht zur Kraft
wird auf beiden Wegen keine Arbeit geleistet, da
dort die Kraft F senkrecht auf dem Weg-Element dr
steht. Es bleiben gleich große Weg-Teile parallel
zur Kraft übrig. Da F = const. ist die Arbeit auf
beiden Teilwegen W = F (z2-z1), d.h. hängt lediglich
von Anfangs- und Endpunkt ab.
Jeden beliebigen Weg III im Kraftfeld kann man in
infinitesimal kleine Wege zerlegen, auf denen
ebenfalls die Differenz (z2-z1) für die Arbeit relevant
ist – und nicht die Form des Weges.
mathematischer Beweis (Annahme : konstante Kraft sei in z-Richtung gerichtet) :
W
  
 F (r ) dr  F
P1  P2  P1
 dz
 F ( z 2  z1 )  F ( z1  z 2 )  0
P1  P2  P1
10
Potentielle Energie (im konservativen Kraftfeld)
Wie wir gesehen haben, hängt in einem konservativen Kraftfeld die Arbeit nur von den
Koordinaten des Anfangs- und Endpunktes einer Bewegung ab. Wir können daher die
potentielle Energie eines Körpers im Punkt P definieren als die Arbeit, die zu leisten
ist, wenn man den Körper von einem Bezugspunkt P0 nach P bringt
WP0  P  
P
P0
  
F (r ) dr  E pot P0   E pot P 
Anmerkung : Beachte das Minus-Zeichen in –Epot(P), da nach Defnition die Arbeit zu
leisten ist (und nicht gewonnen wird), um den Körper von P0 nach P zu bringen. Ein
Körper am Punkt P hat also das Potential (d.h. die Möglichkeit) diese Arbeit wieder zu
gewinnen, indem er nach P0 bewegt wird.
Wenn wir den Bezugspunkt P0 so wählen, dass Epot(P0) = 0, dann gilt :
WP0  P   E pot P 
11
Beispiel : Potentielle Energie im homogenen Kraftfeld (F = const.)
wir wählen den Bezugspunkt P = (0,0,0) und legen z-Richtung parallel zur Kraft :
h
Arbeit :
WA B  WA B '  F  dz  F h
0
z.B. im Schwerefeld der Erde nahe der Oberfläche : F = -mg
W
  mgh
z
B‘
B
h
 potentielle Energie der Schwerkraft :
E pot  mgh
0

F  (0,0, F )
A
12
Energiesatz der Mechanik



F  ma  mv
 
 
 v F  mv v
t2


 
 v F dt   m v v dt
t2

t1



dv
mit : v dt 
dt  dv
dt
mit :
Ekin
1 2
 mv
2
v2


  1
2
2
v
F
dt

m
v
d
v

m
v

v
2
1
t
v
2
1
1

t2

Ekin(v2)

Ekin(v1)
kinetische
Energie



dr
und : v dt 
dt  dr 
dt

t1
r2

 



 v F dt   F dr  E pot (r1 )  E pot (r2 )
t2
t1
r1
Ekin P1   E pot P1   Ekin P2   E pot P2 
EnergieErhaltungssatz
13
Beispiel Energieerhaltung : Schwingung einer Feder
Potentielle Energie
der Schwingung :
D
2
E pot  x    x  x0 
2
x0
x
Ekin
Epot
Ein Körper der Masse m schwingt in x-Richtung unter dem Einfluss einer Kraft F =−D (x-x0).
In jedem Punkt x ist die Gesamtenergie E = Epot+ Ekin = Epot(x = xm) = Ekin(x = 0) = const.
14
Zusammenhang zwischen Kraft und potentieller Energie
Geht man in einem konservativen Kraftfeld vom Punkt P um die infinitesimal kleine
Strecke Δr = (Δx, Δy, Δz) zum Punkt P‘, so ändert sich die potentielle Energie um :
E pot 
E pot
x
x 
E pot
y
y 
E pot
z
z
Anmerkung : Das Vorgehen ist äquivalent zur Näherung einer Funktion y(x) durch Extrapolation
von Punkt y(x) mittels der Tangenten : y(x+x) = y(x) + y/x x  Variation y = y/x x 15
 
andererseits gilt : dW  F dr   dE pot

E pot  Fx x  Fy y  Fz z 
Vergleich mit :
liefert :

E pot
x
E pot 
  Fx ;
E pot
x
x 
E pot
y
E pot
y
  Fy ;

 E pot E pot E pot
F  
;
;
y
z
 x
y 
E pot
z


   E pot

E pot
z
z
  Fz
Kraft
= Gradient der
pot. Energie
Die Kraft zeigt in Richtung der größten (negativen) Variation des Potentials,
d.h. in Richtung des Potential-Minimums
16
Potential und Feldstärke
wir betrachten z.B. das Gravitationspotential

F
sei : ME >> m (Probemasse)
m

r
ME
Definition des Potentials :


1
V r   lim  E pot r 
m 0 m


d.h. Potential V = potentielle Energie „pro Probemasse“

GM
 Gravitationspotential : VG r   
r
 Definition der Feldstärke : Kraft pro Probemasse



 F   E pot r 
 
E 
  V r 
m
m
d.h. die Feldstärke ist
der Gradient des Potentials
17