Lösungen zum Mikro 1 Tutorium

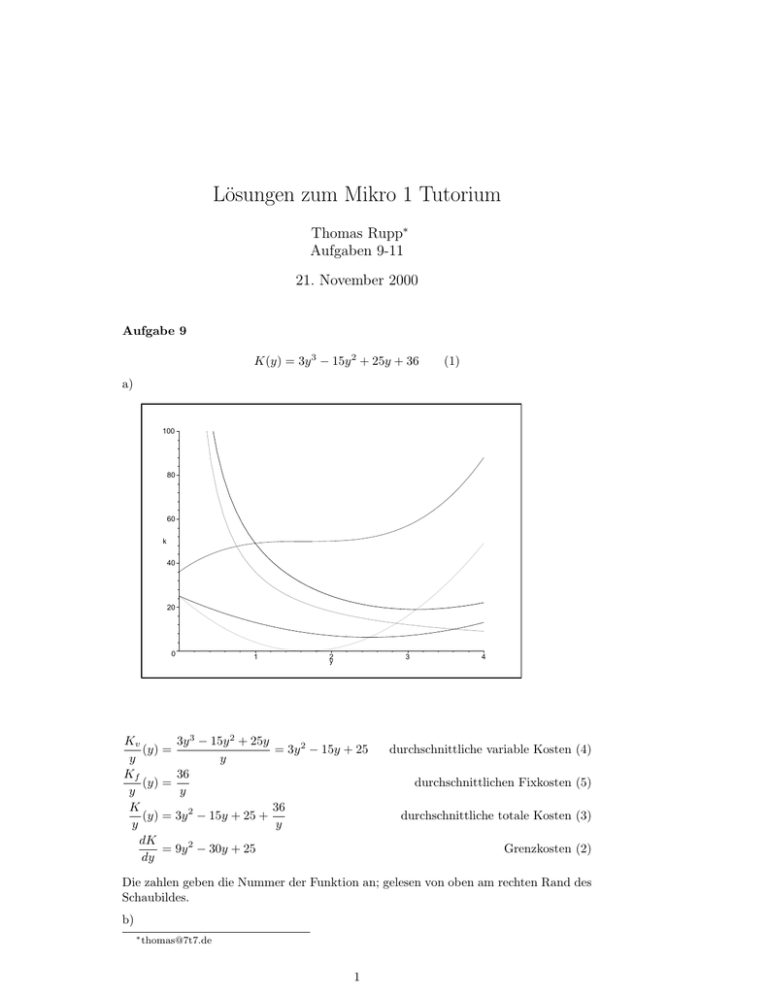
Lösungen zum Mikro 1 Tutorium
Thomas Rupp∗
Aufgaben 9-11
21. November 2000
Aufgabe 9
K(y) = 3y 3 − 15y 2 + 25y + 36
(1)
a)
100
80
60
k
40
20
0
1
2
y
3
3y 3 − 15y 2 + 25y
Kv
(y) =
= 3y 2 − 15y + 25
y
y
Kf
36
(y) =
y
y
K
36
(y) = 3y 2 − 15y + 25 +
y
y
dK
2
= 9y − 30y + 25
dy
4
durchschnittliche variable Kosten (4)
durchschnittlichen Fixkosten (5)
durchschnittliche totale Kosten (3)
Grenzkosten (2)
Die zahlen geben die Nummer der Funktion an; gelesen von oben am rechten Rand des
Schaubildes.
b)
∗ [email protected]
1
2
Rechnen wir also das Minimum (erste Ableitung gleich Null, zweite Ableitung positiv)
der durchschnittlichen variablen Kosten aus:
dKv
5
!
= 6y − 15 = 0 ⇔ 6y = 15 ⇔ y =
dy
2
d2 Kv
=6>0
dy 2
Es werden also y = 2.5 angeboten.
c)
Kv 5
( ) =
y 2
K 5
( ) =
y 2
5
K 0( ) =
2
25
5
25
− 15 + 25 =
4
2
4
Kv 5
Kf 5
25
2
413
( )+
( )=
+ 36 =
y 2
y 2
4
5
20
25
5
25
9 − 30 + 25 =
4
2
4
3
d)
Der Gewinn ist immer Erlös minus Kosten: G(y) = py − K(y) = 16y − (3y 3 − 15y 2 +
25y + 36) = −3y 3 + 15y 2 − 9y − 36. Also wieder das Gewinnmaximum (erste Ableitung
Null, zweite negativ) ausrechnen:
!
G0 (y) = −9y 2 + 30y − 9 = 0 ⇔ y1,2 =
−30 ±
√
302 − 4 · 9 · 9
−18
Denn allgemein besagt die abc-Formel
(mit der pq-Formel gehts natürlich auch), dass
√
−b± b2 −4ac
2
ax + bx + c = 0 ⇔ x1,2 =
.
2a
Wir erhalten also die beiden möglichen y−Werte: y1 = −30+24
= 31 , y2 = −30−24
= 3.
−18
−18
1
Das Schaubild sagt uns schon, dass 3 keinen Sinn macht und wir y = 3 nehmen. Wir
können das anhand der zweite Ableitung verifizieren :G00 (3) = −18 · 3 + 30 = −18 < 0
haben wir bei der Angebotsmenge von 3 ein Gewinnmaximum; bei G00 ( 13 ) = +24 > 0
ein Gewinnminimum.
e)
Beim Deckungsbeitrag (DB) werden nur die variablen Kosten (also nicht die fixen)
betrachtet: DB = py−Kv (3) = 16·3−3·33 +15·32 −25·3 = 48−81+135−75 = 27. Beim
Gewinn werden auch die Fixkosten betrachtet. Also G = py − K(y) = DB − Kf = −9.
Aufgabe 10
Betrachten wir ersteinmal die Standardprozedur. Die Gewinnfunktion ist wie bisher:
1
1
G(y) = py − K(y) = 10y − 40y 2 − 180. Demnach ist dann G0 (y) = 10 − 20y − 2 =
0 ⇔ y = 4. Spätestens jetzt muss auffallen, dass hier etwas nicht stimmt. Betrachten
3
wir die zweite Ableitung, so sehen wir, dass G00 (y) = 10y − 2 > 0. Wir haben also ein
Minimum, in diesem Fall das Gewinnminimum ausgerechnet!
20
Das hätte aber auch gleich auffallen können, denn die Grenzkosten K 0 (y) = √
y sinken!
Also jedes weitere y kostet uns weniger als das vorherige, trägt aber immer p = 10 zum
Erlös bei. Da wir uns im Modell der vollständigen Konkurrenz befinden ist uns der
Preis exogen vorgegeben (und somit konstant, sinkt also nicht) und die volle Abnahme
unserer Produktion ist garantiert. Wir werden deshalb bis an unsere Kapazitätsgrenze
produzieren (also soviel wir können).
Aufgabe 11
3
Beil vollständiger Konkurrenz werden Gewinne immer sofort wegkonkurriert; das bedeutet, dass sobald ein Unternehmen dauerhaft zu einem billigeren Preis anbieten könnte, würde es alle anderen Unternehmen vom Markt verdrängen (das Beste, was dieses
Unternehmen erreichen könnte). Andere Unternehmen können also selber nur zum billigsten Preis aller Unternehmen anbieten. Deshalb sagt man, dass der Preis exogen
(von aussen) vorgegeben ist. Alle Unternehmen können diesen Preis also weder überbieten (dann kauft bei ihnen keiner mehr) noch unterbieten (sonst hätten sie es schon
getan bzw. wir hätten die gleiche Situation, nur mit einem geringeren Preis). Als Fazit
können wir festhalten, dass der Preis ein vorgegebenes Faktum ist und kein Unternehmen Gewinne macht (der Unternehmerlohn, Investitionsgelder, etc. sind in den Kosten
schon dabei).
Weiterhin setzen wir vorraus, dass alle Unternehmen steigende Grenzkosten besitzen
(sonst würden sie unendlich viel bzw. zu einem Preis von Null anbieten). Damit ergibt
sich eine universelle Eigenschaft in Bezug auf vollständige Konkurrenz: denn die
dK
Bedingung für ein Gewinnmaximum lautet ja G0 (y) = p − dK
dy = 0 ⇔ p = dy ; also
Preis gleich Grenzkosten. Da der Preis ja vorgegeben ist, muss jedes Unternehmen
soviel produzieren, bis seine Grenzkosten dem Marktpreis entsprechen.
Ganz allgemein gilt ja, dass der Grenzerlös gleich den Grenzkosten ist. Bei vollständiger Konkurrenz ist aber der Grenzerlös (wieviel bringt die produzierte Einheit an mehr
Umsatz) gleich dem exogenen Preis. Also auch ganz logisch kommen wir bei vollständiger Konkurrenz auf Grenzkosten gleich Grenzerlos gleich Preis.
Die Angebtsfunktion gibt mir an, wieviel ich im Optimum produzieren muss; in Abhängigkeit vom vorgegebenen Preis. Aber das weiss ich bereits: genau soviel, bis meine
Grenzkosten dem Preis entsprechen. Wenn ich also meine Grenzkostenfunktion zeichne,
die ”x-Achse” mit der Menge (y) beschrifte, dann kann ich auf die ”y-Achse” den Preis
(=Grenzkosten) eintragen und so nun ”rückwärts” von einem beliebigen Preis auf die
optimale Menge schließen (ziehe eine Gerade vom Preis parallel zur ”x-Achse” bis zum
Schnittpunkt mit der Grenzkostenfunktion und von dort eine senkrechte Linie. Der
Schnittpunkt mit der ”x-Achse” gibt mir meine optimale Menge an.
Also ist das Schaubild von der Angebotsfunktion identisch mit der Grenzkostenfunktion, wenn ich beide in das gleiche Koordinatensystem zeichne. Das ist gut zu merken.
Nbenbei noch: Mathematisch ist jedoch die Angebotsfunktion die Umkehrfunktion der
Grenzkostenfunktion. Denn für die Grenzkostenfunktion ist die ”x-Achse” die Variable
(die Menge) und sie gibt einen Preis aus; für die Angebotsfunktion ist jedoch die ”yAchse” variabel (der Preis) und sie gibt eine (die optimale) Menge aus. Will man
beide vernünftig in ein Koordinatensystem zeichnen, dann muss man sich für eine
Variable entscheiden und die andere Funktion dahingehend auflösen (umkehren). Also
gilt eigentlich, wenn A(p) die Angebotsfunktion ist:
dK
(y) = A−1 (y).
dy