Der Pomeranchuck Effekt kann zur Kühlung verwendet werden

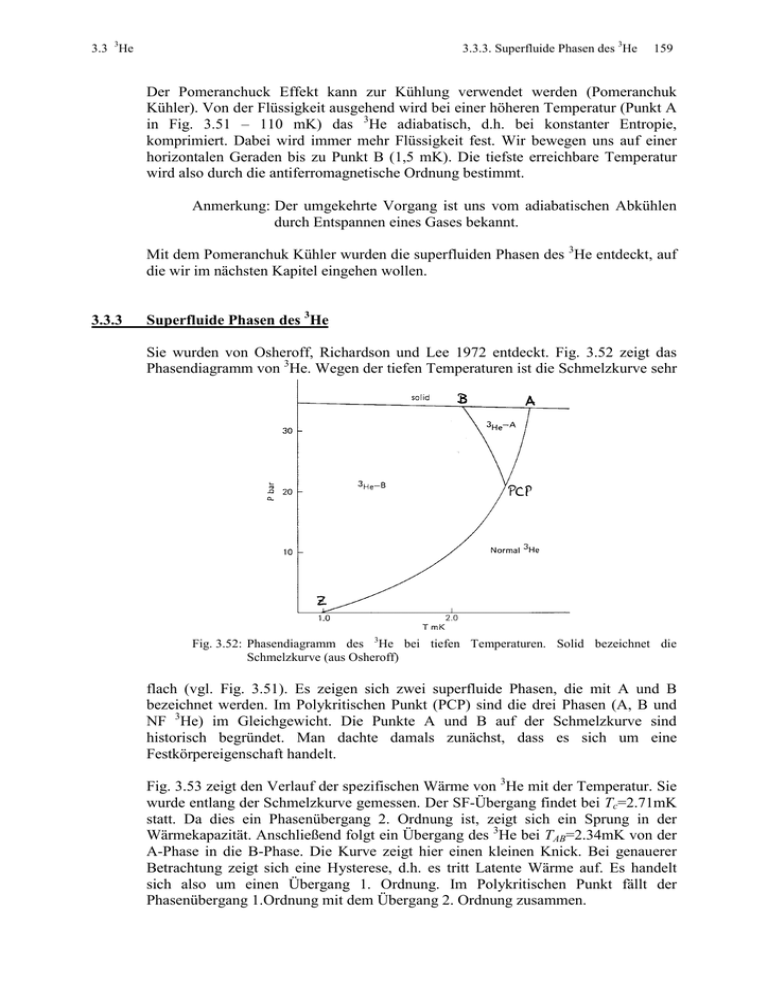
3.3 3He
3.3.3. Superfluide Phasen des 3He
159
Der Pomeranchuck Effekt kann zur Kühlung verwendet werden (Pomeranchuk
Kühler). Von der Flüssigkeit ausgehend wird bei einer höheren Temperatur (Punkt A
in Fig. 3.51 – 110 mK) das 3He adiabatisch, d.h. bei konstanter Entropie,
komprimiert. Dabei wird immer mehr Flüssigkeit fest. Wir bewegen uns auf einer
horizontalen Geraden bis zu Punkt B (1,5 mK). Die tiefste erreichbare Temperatur
wird also durch die antiferromagnetische Ordnung bestimmt.
Anmerkung: Der umgekehrte Vorgang ist uns vom adiabatischen Abkühlen
durch Entspannen eines Gases bekannt.
Mit dem Pomeranchuk Kühler wurden die superfluiden Phasen des 3He entdeckt, auf
die wir im nächsten Kapitel eingehen wollen.
3.3.3
Superfluide Phasen des 3He
Sie wurden von Osheroff, Richardson und Lee 1972 entdeckt. Fig. 3.52 zeigt das
Phasendiagramm von 3He. Wegen der tiefen Temperaturen ist die Schmelzkurve sehr
Fig. 3.52: Phasendiagramm des 3He bei tiefen Temperaturen. Solid bezeichnet die
Schmelzkurve (aus Osheroff)
flach (vgl. Fig. 3.51). Es zeigen sich zwei superfluide Phasen, die mit A und B
bezeichnet werden. Im Polykritischen Punkt (PCP) sind die drei Phasen (A, B und
NF 3He) im Gleichgewicht. Die Punkte A und B auf der Schmelzkurve sind
historisch begründet. Man dachte damals zunächst, dass es sich um eine
Festkörpereigenschaft handelt.
Fig. 3.53 zeigt den Verlauf der spezifischen Wärme von 3He mit der Temperatur. Sie
wurde entlang der Schmelzkurve gemessen. Der SF-Übergang findet bei Tc=2.71mK
statt. Da dies ein Phasenübergang 2. Ordnung ist, zeigt sich ein Sprung in der
Wärmekapazität. Anschließend folgt ein Übergang des 3He bei TAB=2.34mK von der
A-Phase in die B-Phase. Die Kurve zeigt hier einen kleinen Knick. Bei genauerer
Betrachtung zeigt sich eine Hysterese, d.h. es tritt Latente Wärme auf. Es handelt
sich also um einen Übergang 1. Ordnung. Im Polykritischen Punkt fällt der
Phasenübergang 1.Ordnung mit dem Übergang 2. Ordnung zusammen.
3.3 3He
3.3.3. Superfluide Phasen des 3He
160
Fig. 3.53: Verlauf der spezifischen Wärmekapazität mit der Temperatur für 3He (aus Wilks
und Betts)
In Fig. 3.54 ist die zur Viskosität proportionale Resonanzfrequenz eines
Dämpfungsexperimentes in 3He als Funktion der Temperatur aufgetragen. Die Probe
wird von der kritischen Temperatur (1,04 mK; p=0,0 bar, s. Pkt. Z in Fig. 3.52) ab
auf 0,14 mK abgekühlt. Die Grafik zeigt, daß die Viskosität um sechs
Größenordnungen abnimmt, während die normalfluide Komponente ausfriert.
Fig. 3.54: Viskosität des 3He bei 0,0 bar Druck (aus McClintock usw.).
Äquivalent zur Supraleitung, wo zwei Fermionen (Elektronen) ein Cooper-Paar
bilden, paaren sich hier die 3He Atome. Dabei stellen sich jedoch die Spins parallel.
Anders als im SL ist also die Spin-Wellenfunktion symmetrisch und damit nach
Pauli die Ortswellenfunktion antisymmetrisch, also L ungerade. Aus den
Experimenten zeigt sich eindeutig, dass L=1 ist, d.h. wir haben p-Wellen-Paarung.
Fig. 3.55 zeigt die antisymmetrische Ortswellenfunktion (r = Abstand der beiden 3He
–Atome). Der Abstand r=0 wird vermieden, d.h. die Atome „gehen sich aus dem
Weg“. Dadurch ist die Hardcore-Abstoßung geringer als in der normalfluiden Phase
was einer Energieabsenkung entspricht. Dies ist die effektive Paar-Anziehung im
superfluiden 3He, die wir wieder als „Austausch Wechselwirkung“ bezeichnen.
Fig. 3.55 Antisymmetrische Ortswellenfunktion
3.3 3He
3.3.3. Superfluide Phasen des 3He
Anmerkung:
161
Wir kennen die Austausch-Wechselwirkung z.B. vom
Ferromagneten. Hier stellen sich die Spins der Elektronen
parallel. Dadurch wird ebenfalls vermieden, dass sich die
Elektronen überlappen und die Coulomb-Energie wird
abgesenkt.
Wegen der Parallelstellung der Spins hat jedes Paar ein magnetisches Moment.
Daher hängt das Phasendiagramm des SF 3He empfindlich vom Magnetfeld ab:
Fig. 3.56 zeigt das Phasendiagramm des 3He für B=0, 0<B<0.6T und B>0.6T.
Für B>0 tritt an der Grenze zur normalfluiden Phase noch eine zusätzliche A1-Phase
auf und das Existenzgebiet der A-Phase dehnt sich bis nach p=0 aus. Für B>0,6T
verschwindet die B-Phase ganz.
Fig. 3.56: Phasendiagramm des 3He für B=0, 0<B<0.6T und B>0.6T (aus Kent).
Da die beiden Spins parallel sind, gilt für die Spinwellenfunktion S=1. Damit sind
drei Stellungen des Spins im Raum möglich, nämlich: Sz=-1,0,+1. Dies wird
allgemein als ein „Triplett“-Zustand bezeichnet, der für B=0 entartet ist. Im SF 3He
liegt eine Mischung der verschiedenen Sz-Zustände vor. In der Art der Mischung
unterscheiden sich die Phasen A, B oder A1.
Ähnlich wie in der Supraleitung haben alle Paare dieselbe Wellenfunktion. Das
bedeutet auch, daß alle Paare die Triplett-Zustände gleich besetzen. Allgemein kann
die Spin-Wellenfunktion angegeben werden mit:
Ψ = c1 − 1 + c2 0 + c3 + 1
Die verschiedenen Phasen unterscheiden sich in den Koeffizienten ci.
Wir wollen nun auf die einzelnen Phasen eingehen:
Die A-Phase:
Aus dem Experiment erhalten wir c2=0.
a) B=0
Hier sind die Koeffizienten c1 und c3 gleich gewichtet. Es gilt also:
c1 = c3
Damit ergibt sich für den Erwartungswert der z-Komponente des Spins:
áS z = 0
Allerdings wird, obwohl das Feld null ist, intern eine Vorzugsrichtung der zAchse festgelegt, so dass das System anisotrop ist.
3.3 3He
3.3.3. Superfluide Phasen des 3He
162
b) B≠0
Hier wird die Vorzugsrichtung durch das Magnetfeld festgelegt. Aufgrund
des Feldes kommt es zu einer Umlagerung zwischen c1 und c3. Es ist also
c1 ≠ c3 .
Um die Energie zu minimieren stehen mehr Spins in Richtung des Feldes
als entgegengesetzt. Die Flüssigkeit wirkt paramagnetisch
Die A1-Phase:
Wird ein Magnetfeld angelegt, entsteht zwischen der A-Phase und dem NF
Bereich die A1-Phase. Sie zeigt sich bis zu Druck p=0. In Fig. 3.57 ist die
entlang der Schmelzkurve gemessene spezifische Wärmekapazität für B≠0
aufgetragen. Die Temperatur ist in der Grafik auf die kritische Temperatur Tc
normiert. Es zeigt sich ein Sprung in der Wärmekapazität beim Übergang vom
NF in den A1-Bereich und ein weiterer beim Übergang von der A1-Phase in die
A-Phase.
Fig. 3.57: Spezifische Wärmekapazität von 3He entlang der Schmelzkurve. Das Magnetfeld
beträgt 0.88T (aus Wilks und Betts).
In der A1-Phase sind die Koeffizienten c1=c2=0 bzw. c3≠0. Damit ist Sz=1
(„ferromagnetisch“).
Anmerkung:
Es gibt auch eine A2-Phase. Diese zu A1 äquivalente Phase
erhalten wir, wenn das Magnetfeld umgepolt wird (Sz=-1).
Die makroskopische Wellenfunktion in der A1-Phase ist also gegeben mit:
Ψ = c3 + 1
Wie aus Fig. 3.56 zu erkennen ist, ist diese Phase nur in einem schmalen
Temperaturbereich stabil. Sonst ist aufgrund der magnetischen Feldenergie das
Vorliegen beider Spinsorten (+1/-1) energetisch günstiger.
3.3 3He
3.3.3. Superfluide Phasen des 3He
163
Die B-Phase:
a) B=0:
Hier sind alle drei Zustände des Tripletts gleich gewichtet. Wir erhalten
einen isotropen Zustand ohne Vorzugsrichtung.
c1 = c2 = c3
b) B≠0:
Durch Anlegen eines Magnetfeldes verschiebt sich wieder die Gewichtung
der einzelnen Koeffizienten. Da die Komponente mit c2 ≠ 0 unmagnetisch
ist, kann sie kein Diopolmoment ausbilden. Daher ist die Suszeptibiltät der
B-Phase kleiner als die der A-Phase. Die Spins können sich also im
Vergleich zur A-Phase nicht so gut zu einem äußeren Feld einstellen.
Deshalb ist bei höheren Feldern (B>0.6T) die A-Phase bevorzugt.
Anmerkung: Anstelle der hier verwendeten Koeffizienten ci wird in der
Literatur (Leggett) als Nomenklatur der d-Vektor benutzt. Es gilt
der Zusammenhang:
c1 ≡ (d x + id y ) / 2
c2 ≡ d z
c3 ≡ (d x − id y ) / 2
d x = (c1 + c3 ) / 2
bzw.
d y = i (c3 − c1 ) / 2
d z = c2
wobei :
æ dx ö
ç
d = çdy
çd
è z
Der Vorteil des d-Vektors ist, dass in ihm alle drei Komponenten
zusammengefaßt sind und er – im Gegensatz zu den cKoeffizienten – wie ein Vektor bei Rotationen transformiert wird.
Die Koeffizienten legen die Gewichtung des Spinzustandes fest. Damit ist der dVektor der Ordnungsparamter des 3He.
Die di sind im Allgemeinen komplex. Wir können aber eine spezielle Darstellung
wählen, bei der die komplexen Komponenten alle den selben Phasenfaktor
aufweisen. Diesen können wir ausklammern, so dass gilt:
æd ö
H ç x iΘ
d = çdy e
(alle di reell; Θ ≡ Phasenwinkel)
çd
è z
Entsprechend zum SL oder 4He gibt es so nur einen Phasenwinkel. Damit hat d eine
definierte Richtung im Raum. Er stellt sich in jeder der 3He-Phsen in bestimmter
Weise relativ zu B ein. Fig. 3.58 zeigt die Einstellmöglichkeiten des d-Vektors für
die A-Phase (linkes Teilbild) bzw. für die B-Phase (rechtes Teilbild). Während in der
A-Phase der d-Vektor für alle Teilchen immer gleich senkrecht zum Magnetfeld
3.3 3He
3.3.3. Superfluide Phasen des 3He
164
Fig. 3.58: Schematische Darstellung des d-Vektors in 3He für die A-Phase (links) bzw. B-Phase
(rechts). Der Kreis entspricht dabei dem Äquator der Fermikugel. (aus McClintock usw.)
steht, ist der Ordnungsparameter in der B-Phase von der Richtung k des
Wellenvektors der Teilchen abhängig.
Es gibt noch weitere Vektoren, auf die wir im folgenden eingehen wollen.
In der A-Phase ist der Eigendrehimpuls S des Spins parallel zum Feld B. Wie
orientiert sich nun der Einheitsvektor l des Bahndrehimpulses? In Fig. 3.59 ist ein
sich drehendes Paar schematisch gezeigt. Die Atome bewegen sich auf einer
Kreisbahn, wobei ihre Spins S immer parallel zu B „nach oben“ gerichtet sind. Die
Richtung des Bahndrehimpulses l ist senkrecht auf der Kreisbahn, also auch
senkrecht zu S.
Fig. 3.59: Anordnung der Vektoren S bzw. l in der A-Phase des 3He
In der B-Phase liegen ohne Magnetfeld isotrope Verhältnisse vor. Die l-Richtung ist
quantenmechanisch unbestimmt, d.h. es kann keine Aussage darüber gemacht
werden, in welcher Orientierung der Bahndrehimpuls steht. Lediglich der
Gesamtdrehimpuls ist quantenmechanisch bestimmt zu:
J =L+S =0
Da alle d-Vektoren gegen die k-Richtung um 104° verdreht sind (vgl. Fig. 3.58),
stellt die zugehörige Drehachse eine Vorzugsrichtung dar. Sie ist der sogenannte NVektor, der die Textur in der B-Phase bewirkt.
Wird ein Magnetfeld angelegt, stellt sich N parallel zu B ein. Entsprechend ist die
Textur. Ist das Magnetfeld null, so stellt sich die Textur spontan ein. Dazu muß N
(B-Phase) oder l (A-Phase) für alle Paare an einem Ort die selbe Richtung haben.
Eine Beeinflussung von N oder l erfolgt durch die Gefäßwände. Dies zeigt Fig. 3.60
für die A-Phase. Ist die Kreiselfläche des Paars parallel zur Wand, ist dies
energetisch günstiger, als senkrecht zur Wand, da sonst die Atome des Paars „an die
Gefäßwand schlagen“ würden. Damit orientiert sich also l bevorzugt senkrecht zur
Wand (≡Textur).
3.3 3He
3.3.3. Superfluide Phasen des 3He
165
Fig. 3.60: Schematische Darstellung der Kreiselfläche eines Paars senkrecht und parallel zur Wand.
Fig. 3.61 zeigt zwei mögliche Texturbilder der l-Linien innerhalb einer 3He Kugel.
Vergleichen wir beide Bilder, so ist zu erkennen, dass sich die l-Vektoren nicht
immer überall senkrecht zur Wand stellen können. Diese singulären Punkte können
experimentell bestimmt werden.
Fig. 3.61: Mögliche Texturen in der A-Phase des 3He. (aus McClintock usw.)
Bisher haben wir nur Eigenschaften des Grundzustandes betrachtet. Nun wollen wir
auf angeregte Zustände eingehen.
Beim SL repräsentieren die Quasiteilchen (T>0) den angeregten Zustand. Dies sind
einzelne nicht zu Cooper-Paaren gebundene Elektronen. Beim 3He gibt es ebenfalls
Quasiteilchen, also einzelne 3He-Atome. Je höher die Temperatur ist, desto mehr
einzelnen Atome sind vorhanden.
Wir erwarten also auch hier ein Einzelteilchen-Spektrum mit einer Energielücke, da
Energie aufgewendet werden muß, um ein Paar aufzubrechen. Fig. 3.62 zeigt die
Energielücke ∆ als Funktion der k-Richtung für die A-Phase (linkes Teilbild) bzw.
für die B-Phase (rechtes Teilbild). Entsprechend der Anisotropie der A-Phase zeigt
die Energielücke im k-Raum Nullstellen an den Polen bezüglich l. Damit kommt es
in dieser Richtung zu einer hohen Quasiteilchen-Konzentration, also zu einer
„normalfluiden Dichte“. Senkrecht zu l befinden sich wegen der maximalen
Energielücke nur wenig Einzelatome. Aufgrund dieser ungleichen Verteilung der
Atome ist die Normalflüssigkeit richtungsabhängig.
In der B Phase zeigt sich wie beim SL eine isotrope Energielücke und damit eine
richtungsunabhängige Normalflüssigkeit.
3.3 3He
3.3.3. Superfluide Phasen des 3He
166
Fig. 3.62: Energielücke ∆ für die A-Phase (linkes Teilbild) bzw. für die B-Phase (rechtes
Teilbild) (aus McClintock usw.)
Die NF Dichte kann analog zu dem in Fig. 3.16 beschriebenen Experiment bestimmt
werden. Fig. 3.63 zeigt eine Messung der SF-Dichte für unterschiedliche
Magnetfeldrichtungen. (Die NF-Dichte ergibt sich aus 1-ρSF). Aus einer geänderten
B-Feld Richtung folgt eine Änderung der l-Richtung. Damit ändert sich die Richtung
hoher NF Dichte. Deshalb ist die NF-Dichte von der B-Feld Richtung abhängig.
Fig. 3.63: B-Feld-Richtungsabhängigkeit der SF-Dichte (=1-NF-Dichte) in der A-Phase des
3
He. (aus McClintock usw.)
Eine weitere interessante Eigenschaften des 3He sind kollektiven Moden. Diese
ergeben sich aus der Tatsache, dass der Ordnungsparameter aus mehreren
Komponenten besteht. Sie sind im SL nicht zu beobachten, da dort der
Ordnungsparameter nur eine Zahl ist. Diese sollen aber genauso wie NMRExperimente nicht im Rahmen der Vorlesung behandelt werden.
Im nächsten Kapitel wollen wir auf Mischungen von 3He und 4He eingehen.
3.3 3He
3.3.4.
3.3.4. Mischungen von 3He und 4He
167
Mischungen von 3He und 4He
Betrachten wir dazu Fig. 3.64. Gezeigt ist das Phasendiagramm von flüssigen
3
He/4He-Mischungen. Auf der x-Achse ist die Konzentration X des 3He aufgetragen.
Die Konzentration X(3He)=0 entspricht reinem 4He bzw. X(3He)=1 reinem 3He. Auf
der y-Achse ist die Temperatur aufgetragen. Bei hohen Temperaturen ergibt sich der
λ-Punkt für reines 4He zu 2,17K. Wird 3He zugemischt, sinkt der λ-Punkt mit
steigender 3He-Konzentration (vgl. Lambda line). Bei TK=0,87K erreichen wir den
„Trikritischen Punkt“ (tricritical point). Unterhalb von TK bzw. unterhalb der
Phasentrennlinie (phase-separation line) kommt es zur Phasentrennung. Hier
existieren zwei Phasen im Gleichgewicht:
-
3
4
He-reiche Phase. Diese ist leichter und schwimmt damit oben.
He-reiche Phase. Diese ist schwerer und sinkt ab.
Anmerkung: Die Phasengrenze zwischen beiden ist aufgrund der
unterschiedlichen Dichte von 3He und 4He unter dem Winkel der
Totalreflexion optisch beobachtbar.
Wird weiter abgekühlt, setzt sich die Entmischung fort. Bei T=0 sollte vollständige
Entmischung vorliegen. Allerdings zeigt das Experiment, dass bei T=0 noch 6,5%
3
He im 4He verbleiben.
Fig. 3.64: Phasendiagramm von flüssigem 3He/4He-Mischungen
Wieso ist die Entmischung nicht vollständig? Bedeutet ein Rest 3He im 4He eine
endliche Entropie bei T=0, d.h. ist der 3. Hauptsatz verletzt? Dies ist nicht der Fall.
Das 3He bildet im 4He ein Fermigas. D.h. die 3He Atome füllen bei T=0 eine
Fermikugel auf, deren Entropie S=0 ist.
In Fig. 3.65 ist der Verlauf der spezifischen Wärmekapazität für zwei verschiedene
3
He Konzentrationen (X=1,3% bzw. X=5%) in Abhängigkeit von der Temperatur
gezeigt. Das 4He liefert praktisch keinen Beitrag zu Wärmekapazität, da die
3.3 3He
3.3.4. Mischungen von 3He und 4He
Fig. 3.65:
168
spezifische Wärmekapazität als Funktion der Temperatur für verschiedene 3He
Konzentrationen X in 4He (aus Wilks und Betts).
Phononen und Rotonen bei dieser Temperatur alle ausgefroren sind. Für höhere
Temperaturen ergeben sich die klassischen Werte nach dem Dulong-Petit Gesetz.
Bei tieferen Temperaturen ist die spezifische Wärmekapazität c proportional zur
Temperatur T. Die eingezeichnete Linie ergibt sich aus der Theorie des idealen
Fermigases mit der effektiven Masse m* = 2.4m 3 He . Ebenfalls ist die entsprechende
Fermitemperatur angegeben. Wie man es für das ideale Fermigas erwartet, nimmt
danach die Fermitemperatur mit steigender 3He Dichte zu. Über die Konzentration ist
also die Fermitemperatur einstellbar.
Worin liegt nun der Grund für die Restkonzentration von 6,5% des 3He in 4He bei
T=0? Betrachten wir dazu ein 3He-Atom in der 4He Umgebung (Fig. 3.66). Aufgrund
der kleineren Masse hat das 3He-Atom eine stärkere Nullpunktsbewegung als das 4HeAtom. Damit ist das von dem 3He-Atom beanspruchte Volumen in der flüssigen Phase
größer als das der 4He-Atome. Das 3He Atom ist also einem 4He-Atom näher als es
einem anderen 3He Atom sein könnte. Aufgrund dieses geringeren Abstandes ist die
Bindung des 3He-Atoms im 4He stärker als im 3He. Dieses einzelne 3He Atom wird
also bevorzugt im flüssigen 4He gebunden. In Fig. 3.67 ist das chemisches Potenzial
µ3 eines 3He Atoms in reinem 3He bzw. in der 3He-4He-Mischung als Funktion der
3
He-Konzentration x gezeigt. Das chemische Potenzial µ3,c in reinem 3He ist gleich
Fig. 3.66: Schematische Darstellung eines 3He-Atoms in einer 4He Umgebung
3.3 3He
3.3.4. Mischungen von 3He und 4He
169
der latenten Verdampfungswärme L3 je Atom, also
µ3,c=-L3/N0
Der Index „c“ steht für „concentrated“.
Bei der 3He-4He-Mischung (Konzentration x≈0; Index „d“ für „diluted“=verdünnt) ist
die Bindungsenergie eines 3He-Atoms im flüssigen 4He:
ε 3,d ( x = 0) = µ 3,d ( x = 0) / N 0
Dabei ist µ3,d(0) das chemische Potenzial eines 3He-Atoms bei der Konzentration x≈0.
Da die Bindung des 3He-Atoms im 4He stärker als im 3He ist, gilt :
− ε 3,d (0) < − L3 / N 0
Wird die Konzentration der 3He-Atome erhöht, nimmt die Bindungsenergie ε3,d(x) des
3
He-Atoms auf Grund einer anziehenden Wechselwirkung etwas zu, d.h. -ε3,d(x)
nimmt ab. Dies ist in Fig. 3.67 eingezeichnet.
Allerdings gilt für die 3He-Atome das Pauliprinzip. Damit müssen bei
Kozentrationserhöhung die 3He-Atome in einen immer höheren Energiezustand
gebracht werden. Die Fermikugel wächst also. Das chemische Potenzial ist damit:
µ 3,d ( x) = −ε 3,d ( x) + k BTF ( x)
Auch dies zeigt Fig. 3.67. Insgesamt wächst als µ3,d(x), bis bei x=6,5% das chemische
Potenzial der reinen 3He-Flüssigkeit, µ3c erreicht wird. Erst von da ab wird reine 3HePhase gebildet, während sich die Konzentration x in der verdünnten Phase nicht mehr
erhöht. Unterhalb von 6,5% 3He in 4He ist es also günstiger, dieses in das 4He
einzubauen.
Fig. 3.67: Chemisches Potenzial des 3He Atoms in reinem 3He (L3/N0) und in 3He-4He Mischungen als
Funktion der 3He-Konzentration x. Bei x3,d=6,5% erreicht das chemische Potenzial von 3He
in 4He das chemische Potenzial von reinem 3He (aus Pobell).
3
He in verdünnter Lösung im 4He verhält sich bis ca. x=10% als zusätzliche
normalfluide Komponente im 4He. Fig. 3.68 zeigt die NF-Dichte des 4He mit 3,3%
3
He. Die NF-Dichte geht nicht auf Null, da die 3He-Atome nicht ausfrieren können. In
reinem 4He würde die NF-Dichte gegen null gehen.
3.3 3He
3.3.4. Mischungen von 3He und 4He
170
Fig. 3.68: Dichte der NF-Komponente in 4He mit 3,3% 3He als Funktion der Temperatur (aus Wilks
und Betts)
In Fig. 3.69 ist ein zu Fig. 3.39 äquivalentes 2. Schall Experiment bei T=0.45K
gezeigt. Teilbild a) zeigt das Ergebnis für reines 4He. Der Wärmepuls erreicht den
Detektor sehr schnell, da die NF Komponente bei der tiefen Temperatur nur aus
Phononen besteht und diese eine hohe mittlere Geschwindigkeit haben. Denn es war ja
v2 = v / 3 . In Teilbild b) ist das Ergebnis für 4He mit 0,32 % 3He aufgeführt. Der
Wärmepulses trifft später ein, da die massebehaftete 3He-NF-Komponente eine
langsamere mittlere Teilchengeschwindigkeit hat.
Fig. 3.69: 2. Schall Experiment für reines 4He (a) und für 4He mit 0,32% 3He(b). (aus Wilks und Betts)