1 Übersicht Entscheidungsbäume

Übersicht
• Untere Schranken
• Sortieren mit linearem Aufwand
Datenstrukturen & Algorithmen
Matthias Zwicker
Universität Bern
Frühling 2009
2
Wie schnell können wir sortieren?
Entscheidungsbäume
• Bis jetzt: sortieren durch vergleichen
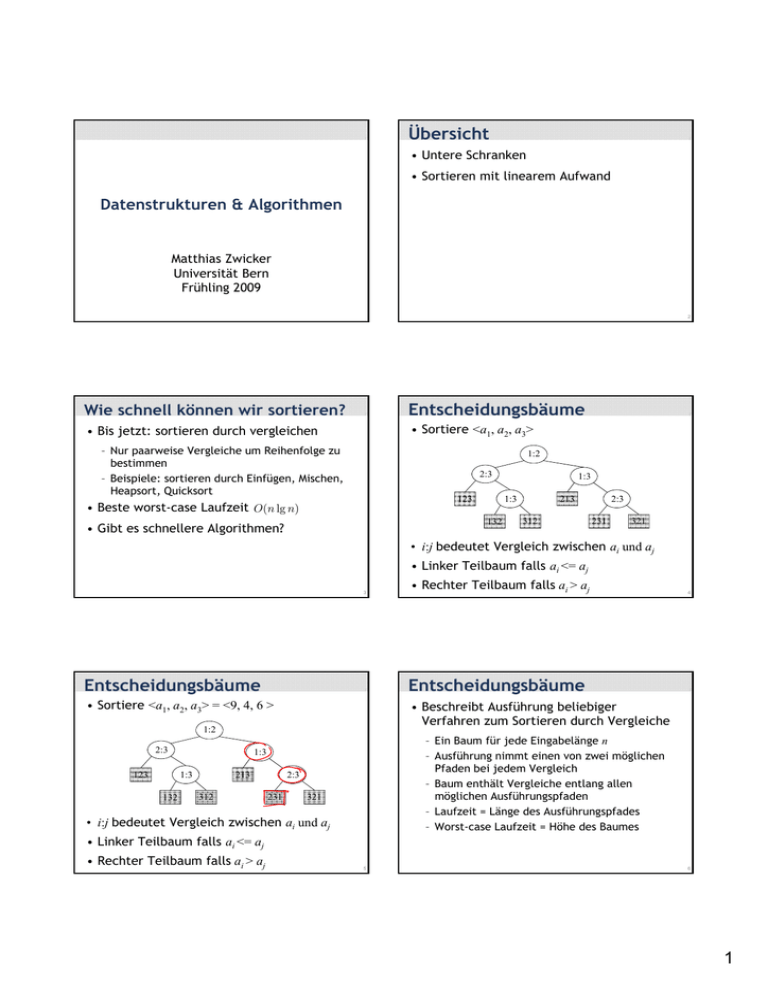
• Sortiere <a1, a2, a3>
– Nur paarweise Vergleiche um Reihenfolge zu
bestimmen
– Beispiele: sortieren durch Einfügen, Mischen,
Heapsort,
p
, Quicksort
1:2
2:3
123
• Beste worst-case Laufzeit O(n lg n)
213
13
1:3
132
• Gibt es schnellere Algorithmen?
1:3
312
23
2:3
231
321
• i:j bedeutet Vergleich zwischen ai und aj
• Linker Teilbaum falls ai <= aj
3
• Rechter Teilbaum falls ai > aj
Entscheidungsbäume
Entscheidungsbäume
• Sortiere <a1, a2, a3> = <9, 4, 6 >
• Beschreibt Ausführung beliebiger
Verfahren zum Sortieren durch Vergleiche
1:2
2:3
123
132
– Ein Baum für jede Eingabelänge n
– Ausführung nimmt einen von zwei möglichen
Pfaden
ade bei
be jedem
jede Vergleich
Ve gle c
– Baum enthält Vergleiche entlang allen
möglichen Ausführungspfaden
– Laufzeit = Länge des Ausführungspfades
– Worst-case Laufzeit = Höhe des Baumes
1:3
213
13
1:3
312
23
2:3
231
4
321
• i:j bedeutet Vergleich zwischen ai und aj
• Linker Teilbaum falls ai <= aj
• Rechter Teilbaum falls ai > aj
5
6
1
Untere Schranke für Sortieren durch Vergleichen
Untere Schranke für Sortieren durch Vergleichen
• Theorem: Jeder Entscheidungsbaum, der n
Elemente sortiert, muss mindestens Höhe
Ω(n lg n) haben
• Folgerung: Heapsort und Sortieren durch
Mischen sind asymptotisch optimale
vergleichende Sortieralgorithmen
• Beweis: Baum hat >=n! Blätter, weil es n!
Permutationen gibt.
gibt Binärbaum der Höhe h
hat <=2h Blätter. Also muss n!<=2h.
h ≥ lg(n!)
≥ lg((n/e)n )
= n lg n − n lg e
= Ω(n lg n)
7
8
Übersicht
Sortieren mit linearem Aufwand
• Untere Schranken
Counting sort: keine Vergleiche zwischen
Elementen!
• Sortieren mit linearem Aufwand
• Eingabe: A[1..n], wobei A[j] ∈{1,2,..,k}
• Ausgabe: B[1..n], sortiert
• Zwischenspeicher: C[1..k]
9
Counting sort
10
Beispiel
1 2 3
4 5
A: 4 1 3 4 3
1 2 3
4
C:
B
B:
11
12
2
Beispiel
1 2 3
Beispiel
4 5
A: 4 1 3 4 3
1 2 3
1 2 3
4
4 5
A: 4 1 3 4 3
C:
1 2 3
1 2 3
B
B:
4
C: 1 0 2 2
4
C´::
C
B
B:
13
Beispiel
1 2 3
Analyse
4 5
A: 4 1 3 4 3
1 2 3
4
C: 1 1 3 5
1 2 3
B
B:
14
4
C´::
C
15
16
Laufzeit
Stabiles Sortieren
• Wenn k=O(n), dann ist Counting Sort Θ(n)
• Counting sort ist stabil
– Reihenfolge gleich grosser Elemente wird nicht
verändert
• Besser als untere Schranke O(n lg n) ?!
• Counting sort ist kein vergleichender
Sortieralgorithms!
1 2 3
– Keine Vergleiche im gesamten Algorithmus
4 5
A: 4 1 3 4 3
B: 1 3 3 4 4
17
18
3
Radix sort
Beispiel
• Ziffer um Ziffer sortieren
• Schlechte Idee: bei der höchstwertigen
Ziffer anfangen
329
• Besser: bei der niederwertigsten Ziffer
anfangen und eine stabile Sortiermethode
verwenden
657
457
839
436
720
355
19
20
Korrektheit
Korrektheit
• Induktion über Position der Ziffern
• Induktion über Position der Ziffern
• Annahme: Zahlen sind bis zu Ziffer t-1 sortiert
• Annahme: Zahlen sind bis zu Ziffer t-1 sortiert
• Induktionsschritt:
Sortiere Ziffer t
• Induktionsschritt:
Sortiere Ziffer t
– Zwei Zahlen, die sich in
Ziffer t unterscheiden
werden korrekt sortiert
720
329
329
355
436
436
839
457
355
657
457
720
657
839
– Zwei Zahlen, die sich in
Ziffer t unterscheiden
werden korrekt sortiert
– Reihenfolge von Zahlen,
die in Ziffer t gleich sind,
wird nicht verändert
=> korrekte Reihenfolge
720
329
329
355
436
436
839
457
355
657
457
720
657
839
21
22
Analyse
Analyse
• Counting sort zum stabilen Sortieren
• Zur Erinnerung: Counting sort braucht
Θ(n + k) um n Zahlen im Bereich 0 bis k-1
zu sortieren
• Sortiere n Binärzahlen mit je b bits
• Interpretiere Zahl als b/r stellige Zahl mit
Ziffern zur Basis 2r
• Beispiel: 32-bit Zahl
8
8
8
• b-bit Zahlen mit r-bit Ziffern
Θ( + 2r )
– Jeder
J d Counting
C
i sort SSchritt
hi b
braucht
h Θ(n
– b/r Schritte (Ziffern)
³
´
– Aufwand T (n, b) = Θ rb (n + 2r )
8
– r = 8 ⇒ b/r = 4 Counting sort Schritte,
Ziffern zur Basis 28
– Alternative: r = 16 ⇒ b/r = 2 Counting sort
Schritte, Ziffern zur Basis 216
• Finde bestes r um T(n,b) zu minimieren
– Grösseres r heisst weniger Counting sort
Schritte, aber exponentielles Wachstum in 2r
23
24
4
Zusammenfassung
Wahl von r
T (n, b) = Θ
³
b
r (n
´
• Radix sort gilt als schnell für grosse Eingaben
+ 2r )
• Beispiel (32-bit Zahlen)
• Ableiten nach r, minimum wo Ableitung 0
– Höchstens 3 Schritte um >2000 Zahlen zu sortieren
– Sortieren ducrch Mischen, Quicksort haben
mindestensdlg 2000e = 11 Schritte
• Für r = lg n ⇒ T (n, b) = Θ(bn/ lg n)
• Für Zahlen in 0 bis nd-11
b = d lg n ⇒ T (n, b) = Θ(dn)
25
26
Zusammenfassung
Ursprung
• Nachteil
• Lochkartensortierer
– Geringe Lokalität der Speicherzugriffe
– Optimierter Quicksort ist häufig schneller in
Praxis
• Erfunden von Herman
Hollerith
• Amerikanische
Volkszählung 1890
• Seine Firma war Teil der Gründung von IBM
27
28
Nächstes Mal
Elementare Datenstrukturen
• Verkettete Listen, Stacks, Bäume
29
5