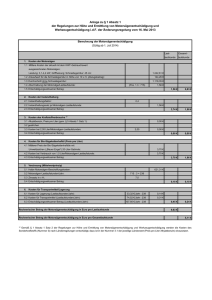
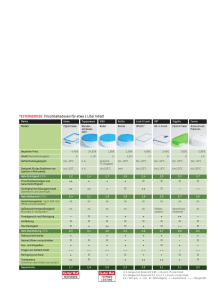
Wochenplan
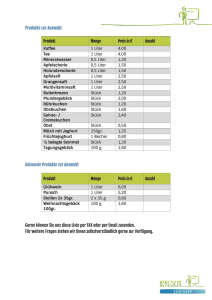
Werbung

Themenübersicht
Arbeitsblatt 1
Statistik
Inhalt,
Schwerpunkte des
Themas
Urliste, Rangliste,
Zentralwert,
Mittelwert,
mittlere Abweichung
Arbeitsblatt 2
Erheben und
Auswerten von Daten
Strichliste,
relative Häufigkeit,
Säulendiagramm
( Histogramm )
Arbeitsblatt 3
Zufallsexperimente
Wahrscheinlichkeit,
einstufige
Zufallsexperimente
Arbeitsblatt 4
mehrstufige
Zufallsexperimente
mehrstufige
Zufallsexperimente,
Baumdiagramm,
Pfadregeln
Kontrolle
Arbeitsblatt 1
Zentralwert – Mittelwert – mittlere Abweichung
Es folgt ein Beispiel zum
Thema! Beispiel durcharbeiten!
Der Benzinverbrauch zweier Autos vom Typ A und B soll im Stadtverkehr getestet
werden. Nach jeder Fahrt ermittelt man, wie viel Liter Benzin jeweils für 100 km
benötigt wurden:
Typ A:
8,0;
7,4;
8,4;
7,8;
9,3;
8,2;
8,6;
7,0;
8,2
Typ B:
8,7;
7,9;
8,4;
8,1;
7,8;
7,9;
8,5;
8,3;
7,6;
7,8
a) Diese Urlisten sind unübersichtlich. Ordne für jeden Typ die Messwerte nach
wachsender Größe! So erhältst du Ranglisten.
b) Welcher Wert steht in der Mitte der Ranglisten von Typ A? Die Rangliste von
Typ B enthält 10 Werte, also eine gerade Anzahl. Die Mitte liegt hier zwischen
dem 5. Und 6. Wert. Bilde den Mittelwert dieser beiden Werte, indem du die
Werte addierst und dann durch 2 teilst. Die auf diese Weise bei Typ A und B
ermittelten Werte nennt man Zentralwert. Vergleiche!
c) Berechne für jedes Auto den mittleren Verbrauch. Addiere zunächst alle
Benzinverbrauchswerte miteinander. Teile dann dein Ergebnis durch die Anzahl
der Stichproben bei jedem Autotyp.
d) Um welche Beträge weichen die einzelnen Werte jeder Liste von ihren Mittelwert
ab? Der Mittelwert dieser Abweichung heißt mittlere Abweichung. Berechne
für jedes Auto die mittlere Abweichung der Testwerte von ihrem Mittelwert!
Vergleiche!
a) Rangliste ( Werte nach der Größe geordnet! )
Typ A:
Typ B:
7,0;
7,6;
7,4;
7,8;
7,8;
7,8;
8,0;
7,9;
8,2;
7,9;
8,2;
8,1;
8,4;
8,3;
8,6;
8,4;
9,3
8,5;
8,7
b) Zentralwert
Typ A:
Typ B:
Zentralwert: 8,2 Liter
Zentralwert: 7,9 + 8,1 = 16 : 2 = 8,0 Liter
Typ A
höherer Verbrauch
c) mittlerer Verbrauch ( Mittelwert! )
Typ A:
Typ A:
Typ B:
Typ B:
(7,0 + 7,4 + 7,8 + 8,0 + 8,2 + 8,2 + 8,4 + 8,6 + 9,3)
9
8,1 Liter
(7,6 + 7,8 + 7,8 + 7,9 + 7,9 + 8,1 + 8,3 + 8,4 + 8,5 + 8,7)
10
8,1 Liter
Verbrauch
gleich!
d) mittlere Abweichung
mittlere
Abweichungen
vom Mittelwert
Typ A
8,0 Liter
7,4 Liter
8,4 Liter
7,8 Liter
9,3 Liter
8,2 Liter
8,6 Liter
7,0 Liter
8,2 Liter
Beispiel zur 1. Aufgabe!
Typ B
- 0,1
- 0,7
+ 0,3
- 0,3
+ 1,2
+ 0,1
+ 0,5
- 1,1
+ 0,1
8,7 Liter
7,9 Liter
8,4 Liter
8,1 Liter
7,8 Liter
7,9 Liter
8,5 Liter
8,3 Liter
7,6 Liter
7,8 Liter
8,0 – 8,1 = - 0,1
mittlere Abweichung Typ A:
mittlere Abweichung Typ A:
mittlere Abweichung Typ B:
mittlere Abweichung Typ B:
mittlere
Abweichung
vom Mittelwert
Beispiel zur 1. Aufgabe!
+ 0,6
- 1,1
+ 0,3
0
- 0,3
- 0,2
+ 0,4
+ 0,2
- 0,5
- 0,3
8,7 – 8,1 = + 0,6
(0,1 + 0,7 + 0,3 + 0,3 + 1,2 + 0,1 + 0,5 + 1,1 + 0,1)
9
0,48888888888 ~ 0,5 Liter
(0,6 + 1,1 + 0,3 + 0,3 + 0,2 + 0,4 + 0,2 + 0,5 + 0,3)
10
0,39 ~ 0,4 Liter
Beim Typ A ist die mittlere Abweichung vom Mittelwert am höchsten!
1. Übung zum Beispiel! ( Gehe wie im Beispiel vor! )
Typ A:
Typ B:
8,6;
7,4;
8,4;
8,1;
7,5;
9,3;
7,4;
8,0;
8,5;
9,3;
8,1;
8,0;
8,6;
8,2;
8,2;
7,9;
9,4
8,4;
7,4
2. Postschalter
Die Anzahl der Kunden an einem Postschalter betrug in 20 aufeinanderfolgenden
Zeitabschnitten von je zehn Minuten
9; 6; 7; 4; 6; 6; 5; 4; 5; 0; 3; 9; 7; 6; 5; 4; 5; 6; 6; 7.
Bestimmt den Zentralwert, berechnet den Mittelwert und die mittlere
Abweichung!
Arbeitsblatt 2
Häufigkeit
Erheben von Daten – absolute Häufigkeit – relative
Ein Unfallstatistik, eine Ausfuhrstatistik, eine Arbeitslosenstatistik usw. ist eine Liste von
Zahlen. In der Mathematik benutzt man die Bezeichnung „Statistik“ umfassenden. Die
Statistik ist ein eigenständiges Teilgebiet der Mathematik, das sich mit dem Erheben und
Auswerten von Daten befasst.
Um die Verkehrsbelastung einer Straße zu ermitteln, führt man eine Verkehrszählung durch.
Dafür legt man folgendes fest: „Personenkraftwagen“ – Pkw;
„Lastkraftwagen“ – Lkw; „Lastzüge“ (Lastkraftwagen mit Anhänger) – Lz;
„Busse“ – Busse; „Motorräder und Mopeds“ – Motorräder.
Die Verkehrsbelastung hängt von der Tageszeit ab. Deshalb teilt man den Zähltag in
Zeitabschnitte von jeweils einer halben Stunde auf. Die Beobachtungen werden in einer
Strichliste festgehalten.
Strichliste
Beispiel:
Ort:
Zeit:
Gaußstraße
6.00 – 6.30 Uhr
Pkw
Lkw
Lz
Busse
Motorräder
absolute
Häufigkeit
IIII IIII IIII IIII IIII IIII IIII
IIII IIII I
IIII
III
II
34
11
5
3
2
Es wurden 34 Pkw gezählt. Statt dessen sagt man auch: Die absolute Häufigkeit der Pkw
ist 34. Die Tabelle zeigt, wie sich die absolute Häufigkeit auf die einzelnen Ergebnisse
verteilen. Man spricht von einer Häufigkeitsverteilung. Die Häufigkeitsverteilung kann durch
ein Säulendiagramm veranschaulicht werden.
40
35
30
25
cm
20
15
10
5
0
Pkw
Lkw
Lz
Busse
Motorräder
Relative Häufigkeit
Beobachtet man unter n Ergebnissen ein bestimmtes Ergebnis E genau x-mal, so
x
heißt der Quotient
die relative Häufigkeit von E.
n
absoluteHäufigkeit
x
Relative Häufigkeit =
;
h (E) = .
Gesamtzahl
n
Eine halbe Stunde später wurde in der Gaußstraße erneut eine Verkehrszählung
vorgenommen.
Beispiel:
In der nächsten halben Stunde lautet die Häufigkeitsverteilung:
Pkw 48, Lkw 15, Lz 9, Busse 3, Motorräder 5.
Die Verkehrsbelastung wurde offensichtlich größer. Die Anzahl der Pkw ist von 34 auf 48
angewachsen. Ist der Anteil dieser Fahrzeuge am Verkehr auch gewachsen?
Dazu müssen wir die relative Häufigkeit berechnen!
6.00 bis 6.30 Uhr
absolute
relative
Häufigkeit x
Pkw
Lkw
Lz
Busse
Motorräder
Summe
34
11
Häufigkeit
6.30 bis 7.00 Uhr
absolute
relative
x
h
34
= 0,62 = 62%
55
11
= 0,20 = 20 %
55
Häufigkeit x
48
15
Häufigkeit
x
h
48
= 0,64 = 64 %
80
15
= ______________
80
5
5
= 0,09 = 9 %
55
9
9
= ______________
80
3
3
= 0,06 = 6 %
55
3
3
= ______________
80
2
2
= 0,03 = 3 %
55
5
5
= ______________
80
80
80
= _______________
80
55
55
= 1,00 = 100 %
55
Wir erkennen: Obwohl die Anzahl der Pkw am stärksten zunahm, ist ihr Anteil am gesamten
Verkehr gesunken.
Vergleiche die anderen Fahrzeuge!
Säulendiagramm ( Histogramm )
100%
86%
90%
80%
70%
60%
50%
40%
30%
20%
20%
9%6%
3%
10%
0%
Pkw
60%
Lkw
Lz
Busse
19%
11%
4%6%
Motorräder
Arbeitsblatt 2
relative Häufigkeit – Diagramme
1. Erbsen
Die Erbsen in 600 Erbsenhülsen wurden gezählt:
Anzahl der Erbsen
Anzahl der Hülsen
a)
b)
c)
d)
1
36
2
84
3
120
4
129
5
102
6
72
7
42
8
15
Wie viele Erbsen waren durchschnittlich in der Hülse? ( Mittelwert )
Berechne die relative Häufigkeit!
Zeichne ein Säulendiagramm ( Histogramm )!
Berechne die mittlere Abweichung vom Mittelwert!
2. Schlafgewohnheiten
400 Willkürlich ausgewählte Erwachsene wurden befragt, wie viele Stunden sie
durchschnittlich nachts schlafen. Man erhielt:
Schlafdauer in Stunden
Anzahl der Erwachsenen
5
22
6
62
7
100
8
150
9
42
10
24
a) Berechne die relative Häufigkeiten!
b) Zeichne ein Säulendiagramm!
c) Welche Schlafdauer kommt bei Erwachsenen
am häufigsten vor? Wird der Mittelwert kleiner
oder größer als dieser häufigste Wert sein?
d) Berechne den Mittelwert!
e) Berechne die mittlere Abweichung vom
Mittelwert!
3. Lufttemperatur
In der folgenden Tabelle sind für drei Orte die Monatsmittelwerte der Lufttemperatur
in C° angegeben:
Januar Februar
Rio de
Janeiro
München
Jakutsk
September
Oktober
26,0 26,1 25,5 23,9 22,3 21,3 20,8 21,1
21,5
22,3
23,1
24,4
- 2,1 - 0,9 3,3 8,0 12,5 15,8 17,5 16,6
-42,7 -36,6 - 23 -6,9 6,6 16,1 19,5 15,5
13,4
6,3
7,9
- 7,9
3,0
- 28,4
- 0,7
- 39,8
März
April
Mai
Juni
Juli
August
November
a) In welchem Monat nimmt die Lufttemperatur an den drei Orten ihren höchsten
Wert an, in welchem Monat ihren niedrigsten?
b) Berechne zu jedem Ort die mittlere Jahrestemperatur!
c) Stelle die Monatsmittelwerte in einem geeignetem Diagramm dar!
Dezember
Arbeitsblatt 3
Zufallsexperimente – Wahrscheinlichkeit
Wenn wir einen Würfel werfen, können wir nicht voraussagen, welche Seitenfläche oben liegen wird.
Es gibt sechs Möglichkeiten.
Ein Experiment, bei dem mehrere Ergebnisse ( Ausfälle ) möglich sind, heißt Zufallsexperiment. Alle
möglichen Ergebnisse eines Zufallsexperimentes fasst man zur Ergebnismenge S zusammen.
1. Beispiel: Werfen einer Münze
Ergebnisse:
Zahl ist oben ( Z ); Wappen ist oben ( W )
S = {Z , W }
Ergebnismenge:
2. Beispiel: Würfeln
Ergebnisse:
Ergebnismenge:
1 fällt, 2 fällt, 3 fällt, 4 fällt, 5 fällt, 6 fällt.
S = {1,2,3,4,5,6}
Sind alle Ergebnisse eines Zufallsexperiments gleichwahrscheinlich, so gilt für die
Wahrscheinlichkeit P eines Ereignisses A:
P(A)=
Anzahl _ der _ Ergebnisse, _ die _ zu _ A _ gehören
Anzahl _ aller _ möglichen _ Ergebnisse
1. Beispiel: Mit welcher Wahrscheinlichkeit werfe ich „keine Sechs“?
P („keine Sechs“) =
5
= 0,83 = 83 %
6
( „keine Sechs“ bedeutet es können
alle anderen Zahlen fallen – 1, 2, 3, 4,
5 – also 5 Zahlen von 6 möglichen )
2.Beispiel:
Mit welcher Wahrscheinlichkeit werfe ich eine „gerade Zahl“?
P („gerade Zahl“) =
3
= 0,5 = 50 %
6
( 3 gerade Zahlen von 6 möglichen )
1. Werfen eines Tetraeders
Bei einem Tetraeder gilt die Zahl als geworfen, auf deren Seite das Tetraeder
liegen bleibt.
a) Gib die Ergebnismenge S an!
Wie groß ist bei einem idealen Tetraeder die Wahrscheinlichkeit für
b) eine 2,
c) keine 2,
d) eine Zahl größer 2,
e) eine gerade Zahl?
2. Ziehen aus einer Urne
Eine Urne enthält 1 weiße Kugel, 2 schwarze Kugeln, 3 rote Kugeln und 4 blaue
Kugeln. In die Urne wird blind hineingegriffen, und eine Kugel wird gezogen.
a) Gib die Ergebnismenge S an!
b) Lege eine Tabelle mit den Ergebnissen an
und trage zu jedem Ergebnis die
Wahrscheinlichkeiten ein!
Wie groß ist die Wahrscheinlichkeit,
c) eine farbige Kugel,
d) keine farbige Kugel zu ziehen?
3.
a)
b)
c)
d)
Ein Skatspiel besteht aus 32 Karten. Wie groß ist die Wahrscheinlichkeit,
das Herz-As,
eine Herzkarte,
ein As,
eine Lusche ( Sieben, Acht, Neun ) zu ziehen?
4. In einem Behälter sind 60 Kugeln. Sie sind von 1 bis 60 nummeriert. Eine Kugel
wird gezogen. Berechne die Wahrscheinlichkeit für folgender Ereignis:
a) Die Zahl ist durch 3 teilbar.
b) Die Zahl ist Vielfaches von7.
c) Die Zahl ist gerade.
d) Die Zahl ist ein Teiler von 60.
e) Die Zahl ist eine Primzahl.
f) Die Zahl enthält zwei gleiche Ziffern.
g) Die Zahl ist zweistellig.
h) Die Zahl enthält die Ziffer 5.
Lege vier Streichhölzer so dazu,
dass fünf Quadrate entstehen!
Lege zwei Streichhölzer so um, dass
vier kongruente gleichseitige Dreiecke
entstehen!
Arbeitsblatt 4
Mehrstufige Zufallsexperimente – Baumdiagramm
Wird ein Zufallsexperiment mehrmals hintereinander ausgeführt, so spricht man von einem
mehrstufigen Zufallsexperiment. Mit einem Baumdiagramm können wir die möglichen Ergebnisse
und die Wahrscheinlichkeiten finden.
1. Beispiel: Eine Münze wird zweimal geworfen.
1. Wurf
2. Wurf
Ergebnisse
Z
W
Z
W
Z
W
ZZ
ZW
WZ
WW
1
4
1
4
1
4
1
4
Jeder Weg vom Start bis zu
Einem Endpunkt liefert ein
Ergebnis. Also treten die vier
Ergebnisse ZZ, ZW, WZ, WW
auf. Legt man auf den
Startpunkt vier Plättchen und
verteilt diese längst der Wege
gemäß den
Wahrscheinlichkeiten , so
kommt in jedem Endpunkt ein
Plättchen an. Eines von vier
Plättchen bedeutet, dass die
Wahrscheinlichkeit 14 ist.
Wahrscheinlichkeiten
1
für die Wahrscheinlichkeiten eines Ergebnisses erhält man auch,
4
wenn man die Wahrscheinlichkeiten multipliziert.
Den Wert
Eine Münze wird dreimal nacheinander geworfen.
a) Zeichne ein Baumdiagramm! Gib alle Ergebnisse und ihre Wahrscheinlichkeiten
an!
b) Wie groß ist die Wahrscheinlichkeit zunächst Z, dann W und schließlich noch
einmal W zu werfen ( Ergebnis ZWW )?
c) Wie groß ist die Wahrscheinlichkeit für WZW bzw. WWZ?
d) Wie groß ist die Wahrscheinlichkeit für das Ereignis „ohne Berücksichtigung der
Reihenfolge wird einmal Z und zweimal W“ geworfen?
Arbeitsblatt 4
1. Pfadregel ( Produktregel ):
Die Wahrscheinlichkeit eines Pfades ist gleich dem Produkt der
Wahrscheinlichkeiten entlang des jeweiligen Pfades im Baumdiagramm.
2. Pfadregel ( Summenregel ):
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der
Wahrscheinlichkeiten aller der Pfade, die für dieses Ereignis günstig sind.
1. Ein idealer Würfel wird zweimal nacheinander geworfen.
a) Zeichne ein Baumdiagramm! Gib alle Ergebnisse und ihre Wahrscheinlichkeiten
an!
b) Welche Ergebnisse liefern die Augensumme 11?
Wie groß ist die Wahrscheinlichkeit für das Ereignis „Augensumme 11“?
c) Wie groß ist die Wahrscheinlichkeit für das Ereignis „Augensumme 7“?
2. Raten bei einem Test
Ein Auswahltest besteht aus vier Aufgaben. Jede Aufgabe enthält vier Antworten,
von denen jeweils eine richtig ( r ) und drei falsch ( f ) sind. Peter hat im Unterricht
nicht aufgepasst und nichts gelernt. Er kreuzt bei jeder Frage eine Antwort zufällig
an.
a)
b)
c)
d)
Zeichne ein Baumdiagramm!
Mit welcher Wahrscheinlichkeit kreuzt Peter alle vier Aufgaben richtig an?
Mit welcher Wahrscheinlichkeit kreuzt er drei Aufgaben richtig an?
Der Test gilt als bestanden, wenn mehr als die Hälfte der Aufgaben richtig
angekreuzt wurden. Wie groß ist die Wahrscheinlichkeit, dass Peter den Test
besteht?