Mathematik verstehen 8 Stammfunktionen Lösungsblatt Aufgabe

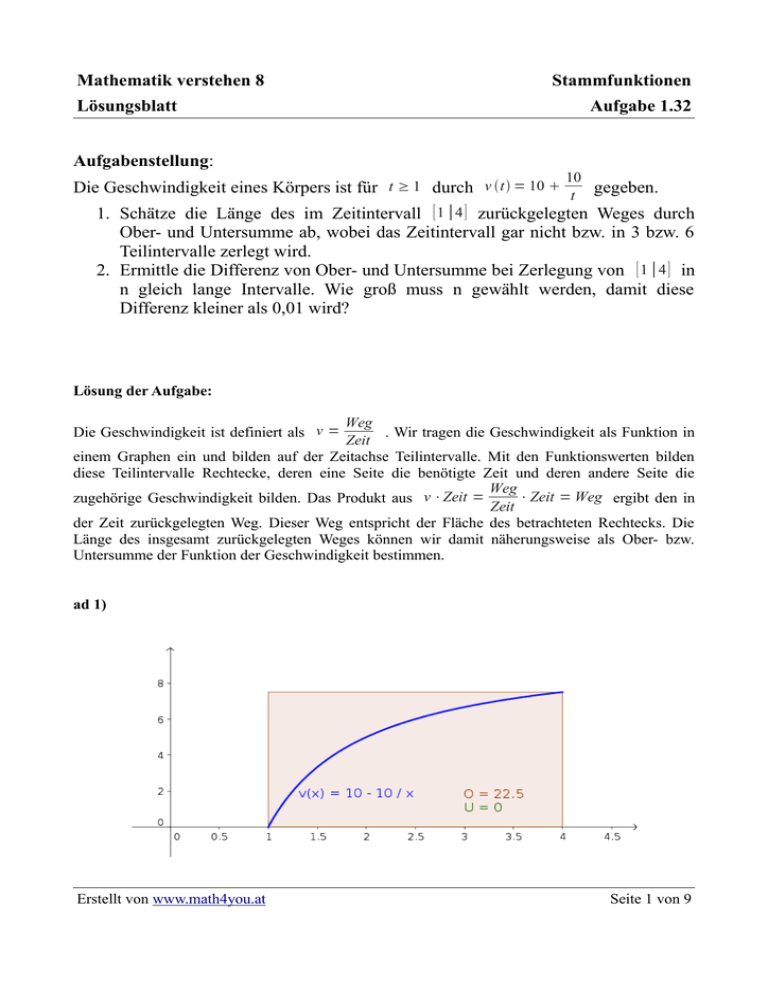
Mathematik verstehen 8
Lösungsblatt
Stammfunktionen
Aufgabe 1.32
Aufgabenstellung:
10
Die Geschwindigkeit eines Körpers ist für t ≥ 1 durch v t = 10  t gegeben.
1. Schätze die Länge des im Zeitintervall [ 1 ∣4 ] zurückgelegten Weges durch
Ober- und Untersumme ab, wobei das Zeitintervall gar nicht bzw. in 3 bzw. 6
Teilintervalle zerlegt wird.
2. Ermittle die Differenz von Ober- und Untersumme bei Zerlegung von [ 1 ∣4 ] in
n gleich lange Intervalle. Wie groß muss n gewählt werden, damit diese
Differenz kleiner als 0,01 wird?
Lösung der Aufgabe:
Weg
. Wir tragen die Geschwindigkeit als Funktion in
Zeit
einem Graphen ein und bilden auf der Zeitachse Teilintervalle. Mit den Funktionswerten bilden
diese Teilintervalle Rechtecke, deren eine Seite die benötigte Zeit und deren andere Seite die
Weg
⋅ Zeit = Weg ergibt den in
zugehörige Geschwindigkeit bilden. Das Produkt aus v ⋅Zeit =
Zeit
der Zeit zurückgelegten Weg. Dieser Weg entspricht der Fläche des betrachteten Rechtecks. Die
Länge des insgesamt zurückgelegten Weges können wir damit näherungsweise als Ober- bzw.
Untersumme der Funktion der Geschwindigkeit bestimmen.
Die Geschwindigkeit ist definiert als v =
ad 1)
Erstellt von www.math4you.at
Seite 1 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
Das Intervall [ 1 ∣4 ] hat die Länge 3, d.h. wenn wir das Intervall nicht in Teilintervalle teilen, hat
das zu betrachtende Teilintervall die Länge 3.
Für die Berechnung der Obersumme ist der Funktionswert an der Stelle x = 1  3 zu berechnen:
f 4  =
10 
10
4
7,5
=
Berechnung der Obersumme:
O
=
f  4⋅3
22,5
=
Für die Berechnung der Untersumme ist der Funktionswert an der Stelle x = 1 zu berechnen:
f 1 =
10 −
10
1
0
=
Berechnung der Untersumme:
U
Erstellt von www.math4you.at
=
f 0⋅ 3
=
0
Seite 2 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
Das Intervall [ 1 ∣4 ] hat die Länge 3, d.h. wenn wir das Intervall in drei gleich lange Teile teilen,
hat jedes Teilintervall die Länge 1.
Für die Berechnung der Obersumme sind die
x = 1  1, x = 1  2 und x = 1  3 zu berechnen:
f 2
=
f 3
=
f 4  =
10
2
10
10 −
3
10
10 −
4
10 −
Funktionswerte
=
5
=
6,6667
=
7,5
an
den
Stellen
Berechnung der Obersummen:
O1
O2
O3
=
=
=
f 2⋅1
f 3⋅1
f 4 ⋅1
=
=
=
5
6,6667
7,5
O
=
O 1  O 2  O3
=
19,1667
Für die Berechnung der Untersumme sind die Funktionswerte an den Stellen x = 1, x = 2 und
x = 3 zu berechnen:
Erstellt von www.math4you.at
Seite 3 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
f 1 =
f 2 =
f 3 =
10
1
10
10 −
2
10
10 −
3
10 −
=
0
=
5
=
6,6667
Berechnung der Untersummen:
U1
U2
U3
=
=
=
f 2⋅1
f 3⋅1
f  4⋅1
=
=
=
0
5
6,6667
U
=
U 1  U2  U3
=
11,6667
Erstellt von www.math4you.at
Seite 4 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
Das Intervall [ 0 ∣3 ] hat die Länge 3, d.h. wenn wir das Intervall in sechs gleich lange Teile teilen,
1
hat jedes Teilintervall die Länge
.
2
Für die Berechnung der Obersumme
x = 1.5, 2, 2.5, 3, 3.5, 4 zu berechnen:
sind
f 1,5 =
10 −
f 2
=
10 −
f 2,5 =
10 −
f 3
=
10 −
f 3,5 =
10 −
f 4 
10 −
=
10
1,5
10
2
10
2,5
10
3
10
3,5
10
4
die
=
Funktionswerte
an
den
Stellen
3,3333
= 5
=
6
=
6,6667
= 7,1429
= 7,5
Berechnung der Obersummen:
Erstellt von www.math4you.at
Seite 5 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
O1
=
O2
=
O3
=
O4
=
O5
=
O6
=
O
=
1
⋅
2
1
⋅
2
1
⋅
2
1
⋅
2
1
⋅
2
1
⋅
2






10 −
10 −
10 −
10 −
10 −
10 −
O1  O 2    O 6
Für die Berechnung der Untersumme
x = 1, 1.5, 2, 2.5, 3, 3.5 zu berechnen:
f 1






10
1,5
10
2
10
2,5
10
3
10
3,5
10
4
sind
=
10 −
f 1,5 =
10 −
f 2
=
10 −
f 2,5 =
10 −
f 3
=
10 −
f 3,5 =
10 −
10
1
10
1,5
10
2
10
2,5
10
3
10
3,5
=
1,6667
=
2,5
=
3
=
3,3333
=
3,5714
=
3,75
=
17,8214
die
Funktionswerte
=
0
=
3,3333
an
den
Stellen
= 5
=
6
=
6,6667
= 7,1429
Berechnung der Untersummen:
Erstellt von www.math4you.at
Seite 6 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
U1
=
U1
=
U2
=
U3
=
U4
=
U5
=
U
=
Erstellt von www.math4you.at
1
⋅ f 1
2
1
⋅ f 1,5 
2
1
⋅ f 2
2
1
⋅ f 2,5
2
1
⋅ f 3
2
1
⋅ f 3,5
2
U1  U2    U 6
=
0
=
1,6667
=
2,5
=
3
=
3,3333
=
3,5714
=
14,0714
Seite 7 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
ad 2)
4−1 3
=
n
n
Teilen wir das Intervall [ 1 ∣4 ] in n gleich lange Teile, hat ein Teilintervall die Länge
Zur Berechnung der Obersumme benötigen wir die Funktionswerte an den Stellen
3
x = 1  i⋅ , i = 1, 2,  , n . Damit ergibt sich für die Obersumme:
n
O=
[  



3
3
3
3
⋅ f 1
 f 1  2⋅    f 1   n − 1  ⋅  f  4 
n
n
n
n
]
Zur Berechnung der Untersumme benötigen wir die Funktionswerte an den Stellen
3
x = 1  i⋅ , i = 0, 2,  , n−1 . Damit ergibt sich für die Untersumme:
n
U=
[
 

3
3
3
⋅ f 1   f 1 
   f 1  n − 1 ⋅
n
n
n
]
Wir berechnen nun die Differenz von Ober- und Untersumme:
O−U
−
=
=
=
[  
[  



]
3
3
3
3
⋅ f 1
 f 1  2⋅    f 1  n − 1  ⋅  f  4  −
n
n
n
n
=

3
3
3
⋅ f 1 f 1
   f 1  n − 1 ⋅
n
n
n
3
⋅ [ f  4  − f 1  ]
n
3
⋅ [ 7,5 − 0 ]
n
22,5
n
]
=
=
=
Die Differenz zwischen Ober- und Untersumme soll kleiner als 0,01 sein, d.h. es soll gelten:
Erstellt von www.math4you.at
Seite 8 von 9
Mathematik verstehen 8
Stammfunktionen
Lösungsblatt
Aufgabe 1.32
O−U
22,5
n
22,5
0,01

0,01

0,01 |⋅

n
2250

n
n
0,01
Wenn n  2250 ist, dann wird die Differenz zwischen Ober- und Untersumme kleiner als 0,01.
Erstellt von www.math4you.at
Seite 9 von 9