2. Potentialströmungen

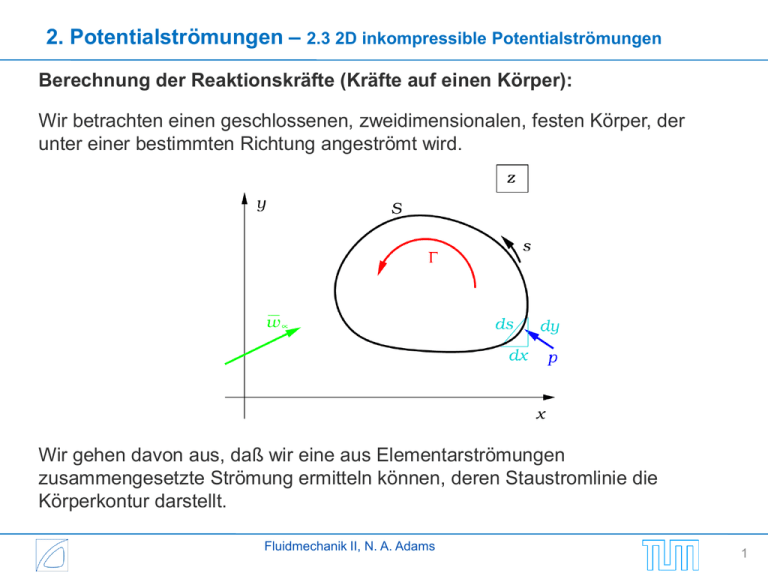
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Berechnung der Reaktionskräfte (Kräfte auf einen Körper):
Wir betrachten einen geschlossenen, zweidimensionalen, festen Körper, der
unter einer bestimmten Richtung angeströmt wird.
Wir gehen davon aus, daß wir eine aus Elementarströmungen
zusammengesetzte Strömung ermitteln können, deren Staustromlinie die
Körperkontur darstellt.
Fluidmechanik II, N. A. Adams
1
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Auf ein Kurvenelement
ds
wirkt die Druckkraft:
dK x = − pdy
dK y = pdx
Damit läßt sich das komplexe Kraftinkrement bestimmen als:
dK =
dK x − idK y =
−ip ( dx − idy ) =
−ipd z
i 2 pdy − ipdx =
Die resultierende Druckkraft auf den umströmten Körper erhält man also durch
Integration entlang der geschlossenen Körperkontur:
K =−
K x iK y =
−i ∫ pd z
∫ dK =
Oft läßt sich nur die Druckdifferenz zum Umgebungsdruck bestimmen p − p∞ .
Da der Umgebungsdruck konstant ist, liefert er keinen Beitrag zur Kraft (das
geschlossene Kurvenintegral verschwindet), also kann man auch schreiben:
K =−
K x iK y =
−i ∫ ( p − p∞ ) d z
∫ dK =
Fluidmechanik II, N. A. Adams
2
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Bei verschwindender Volumenkraft liefert die Bernoulli-Gleichung:
ρ 2
ρ 2
p+ q =
p∞ + U ∞ =
C=
const
2
2
Der Geschwindigkeitsbetrag läßt sich direkt aus dem komplexen Potential
bestimmen:
dF dF dF dF
=
q ww
=
=
dz dz dz d z
2
Eingesetzt in die Bernoulli-Gleichung erhält man:
ρ 2
ρ dF dF
p =−
C
q =−
C
2
2 dz d z
Fluidmechanik II, N. A. Adams
3
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Für die Kraft entlang einer beliebigen geschlossenen Kontur erhält man damit:
K = −i ∫ pd z
dF
K = ∫
dF
dz
Box 37: Körperkraft
Die Körperkontur ist eine Stromlinie, d.h. entlang der Körperkontur
Stromfunktion konstant: ∂ψ
∂s
S
ist die
=0
S
Fluidmechanik II, N. A. Adams
4
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
 ∂φ ∂ψ 
dF
=
 +i

S
∂s  S
 ∂s
Box 37: Körperkraft
Man erhält die Blasius-Formel (Heinrich Blasius, 1883-1970, Doktorand von
Prandtl):
ρ  dF 
K = i ∫ 
 dz
2  dz 
2
Fluidmechanik II, N. A. Adams
(2.17)
5
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Die Blasius-Formel erlaubt noch keine direkte Berechnung der Luftkräfte mittels
des komplexen Potentials. Je nach Ausdruck für das komplexe Potential kann
der Integrand recht kompliziert werden. Von Interesse ist, ob sich diese
Berechnung wesentlich vereinfachen läßt.
Bei der Modellierung von Körperumströmungen werden in der Regel
Elementarströmungen verwendet (Quelle / Senke, Dipol, Potentialwirbel) deren
Singularität von der Körperkontur umschlossen wird.
Aus der komplexen Analysis ist bekannt, daß zur Auswertung des Kurvenintegrals
in (2.17) der spezielle Integrationsweg gleichgültig ist, solange alle Singularitäten,
die zu der modellierten Strömung gehören.
Es ist also nicht nötig, daß der Integrationsweg mit der Körperkontur
übereinstimmt.
Fluidmechanik II, N. A. Adams
6
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Wir gehen davon aus, daß das komplexe Potential durch uns bekannten
Elementarströmungen dargestellt wird, also gilt für die komplexe Geschwindigkeit:
Γl
Qm
Mn
dF
i
1
1
W∞ −
=
+ ∑
− ∑
∑
dz
2π l z − zl 2π m z − zm π n ( z − zn )2
Parallelströmung
Potentialwirbel
Quellen,
Senken
Die Singularitäten der Elementarströmungen
umströmten Körpers.
Dipole
zl ,zm ,zn
liegen im Inneren des
Die komplexe Analysis sagt nun aus (Resdiuenkalkül), daß
2

 dF 
 dF  
∫  dz  dz = 2πi  Summe aller Residuen von  dz  


2
Fluidmechanik II, N. A. Adams
7
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Kurz zusammengefaßt besteht die weitere mathematische Vorgehensweise nun in:
1. Verschiebe den Ursprung des Koordinatensystems in das Körperinnere
(dadurch verschieben sich die Singularitäten der Elementarströmungen).
2. Entwickle die Elementarströmungen in dem Ausdruck für
Laurent-Reihen bezüglich des Ursprungs, also z.B.:
3. Setze
dF / dz jeweils als
 1 zm zm2

Qm
= Qm  + 2 + 3 +  
z − zm
z
z z

Mn
 1 2 zn

=
M
+
+

n 2

2
3
z
z


z
z
−
( n)
2
dF
 dF 
wieder zusammen und bilde 

dz
dz


Fluidmechanik II, N. A. Adams
8
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
z 2 ,1 / z 3 , liefern für geschlossene Kurvenintegrale
1
1
=
, ∫ 3 dz 0 ,
∫ z 2 dz 0=
z
Nur Terme mit 1 / z liefern Residuen für geschlossene Kurvenintegrale.
4. Alle Beiträge mit1 /
Man erhält also:
2

 dF 
 dF  
2πi  Summe aller Residuen von 
  =
∫  dz  dz =

 dz  

 Γ  1
= 2W∞  −i  ∫ dz
 2π  z
2
Wobei die (reelle) Gesamtzirkulation die Summe aller Zirkulationen der
Elementar-Potentialwirbel ist:
Γ=
∑Γ
l
l
Fluidmechanik II, N. A. Adams
9
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Dieses Ergebnis eingesetzt in die Blasius-Gleichung liefert:
ρ  dF 
Γ 1
K=
i ∫ 
ρW∞
dz =
iρW∞ Γ
 dz =

∫
2  dz 
2π z
⇒
K=
iρ (U ∞ − iV∞ ) Γ
2
(2.18)
Dies ist die Kutta-Joukowksi Formel (Martin Kutta 1867-1944, Nikolai Zhukovsky
1847-1921) zur Berechnung der resultierenden Luftkraft auf einen geschlossenen
Körper.
Fluidmechanik II, N. A. Adams
10
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Es ist zweckmäßig, die Kraft in eine Komponente senkrecht und eine parallel zur
Anströmung zu zerlegen:
Man bezeichnet:
L
als Auftrieb, dies ist die Kraftkomponente senkrecht zur physikalischen
Anströmungsgeschwindigkeit W .
∞
D
als Widerstand, dies ist die Kraftkomponente parallel zur physikalischen
Anströmgeschwindigkeit W∞.
Die physikalische Kraft ist das konjugiert Komplexe der komplexen Kraft:
K = K x + iK y = ρV∞ Γ − iρU ∞ Γ
Fluidmechanik II, N. A. Adams
11
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Box 38: Körperkraft
Fluidmechanik II, N. A. Adams
12
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Der Widerstand in einer 2D inkompressiblen Potentialströmung ist :
U∞
V∞
D = ρV∞ Γ
− ρU ∞ Γ
=0
q∞
q∞
(2.19b)
Der Auftrieb in einer 2D inkompressiblen Potentialströmung ist :
U∞
V∞
− ρV∞ Γ
= −ρq∞ Γ
L = −ρU ∞ Γ
q∞
q∞
(2.19a)
Zweidimensionale Potentialströmungen haben also keinen Widerstand.
Dies bezeichnet man als das d‘Alembertsche Paradoxon (Jean-Baptiste
d‘Alembert 1717-1783), da es der experimentellen Erfahrung widerspricht, obwohl
das bestimmte Geschwindigkeitsfeld gut mit dem experimentell gemessenen
übereinstimmt.
Die Auflösung ist: in 2D Reibung, in 3D Reibung und induzierter Widerstand.
Fluidmechanik II, N. A. Adams
13
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Methode der konformen Abbildung:
Der Riemannsche Abbildungssatz (Bernhard Riemann 1826-1866) sagt aus,
daß es eine eindeutige Abbildung z ↔ z ′gibt, für die der geschlossene Bereich
mit der Berandung S das Bild eines Kreises mit der Berandung S ′ ist. Diese
Abbildung ist analytisch und mit Ausnahme von S ′ konform, d.h. winkeltreu.
Fluidmechanik II, N. A. Adams
14
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Folgerungen:
z ′stellt ein komplexes Potential in z dar.
Potential- und Stromlinien in z ′ werden in Potential- und Stromlinien in z
1. Ein komplexes Potential in
2.
abgebildet.
3. Die komplexe Geschwindigkeit kann direkt umgerechnet werden:
dF dF dz ′
1
w (=
z) =
= w ( z′)
df
dz dz ′ dz
dz ′
Fluidmechanik II, N. A. Adams
(2.20)
15
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Eine besonders wichtige Abbildung ist die Joukowski-Abbildung
R2
z= f ( z ′ )= z ′ +
z′
(2.21)
mit den Eigenschaften:
df / dz ′ =⇒
0 z′ =
± R müssen auf dem Rand S ′ liegen.
iϑ′
′
0 in z
=
z
Re
Der Kreis S ′
wird auf das Intervall −2 R ≤ x ≤ 2 R , y =
iϑ′
-iϑ′
z
=
Re
−
R
e
=2 R cos ϑ
abgebildet: S
1. Kritische Punkte
2.
Box 39: Joukowski Abbildung
Fluidmechanik II, N. A. Adams
16
2. Potentialströmungen
• Welche Elementarströmungen liefern einen Beitrag zur resultierenden
Kraft und welche nicht ?
• Was sagt die Kutta-Joukowski-Formel aus ?
• Wie sind Auftrieb und Widerstand definiert ?
• Wie groß ist der Widerstand in einer zweidimensionalen
Potentialströmung ?
• Was leistet die Joukowski-Abbildung ?
Fluidmechanik II, N. A. Adams
17