File - TÜ-Schaltungstechnik 1

Grundlagenorientierungsprüfung für
Elektro- und Informationstechnik
Schaltungstechnik 1 (Wdh.)
Univ.-Prof. Dr. techn. Josef A. Nossek
Freitag, den 16.04.2010
9:00–10:30 Uhr
Name:
Vorname:
Matrikel-Nr.:
Hörsaal:
Platz-Nr.:
• Dieses Aufgabenheft hat 14 Seiten.
• Die Gesamtzahl der Punkte beträgt 90.
• Als Unterlagen für die Prüfung sind maximal 5 beliebig beschriebene Blätter DIN A4 erlaubt.
• Taschenrechner und Mobiltelefone sind nicht zugelassen.
• Mit * gekennzeichnete Aufgaben sind ohne Kenntnis des Ergebnisses der vorhergehenden Teilaufgaben lösbar.
• Es werden nur solche Ergebnisse gewertet, bei denen der Lösungsweg erkennbar ist!
Technische Universität München
Lehrstuhl für Netzwerktheorie und Signalverarbeitung
Univ.-Prof. Dr. techn. Josef A. Nossek
2
Aufgabe 1
Knotenspannungsanalyse
(23 Punkte)
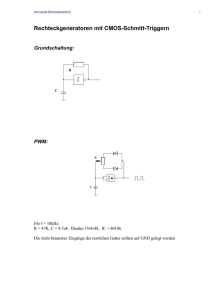
In Bild 1 sei eine, aus ohmschen Widerständen, einem idealen Operationsverstärker,
unabhängigen Quellen und einer gesteuerten Quelle bestehende, Schaltung gegeben. Es wird
angenommen, dass der Operationsverstärker im streng linearen Bereich betrieben wird. Mit Hilfe
der Knotenspannungsanalyse soll die Schaltung untersucht werden.
G1
i2
u1
G3
1
4
3
gm u
2
G2
u
G4
u4
Bild 1. Operationsverstärkerschaltung
a)* In der gegebenen Schaltung lässt sich jede Spannung und jeder Strom als Summe der
Reaktionen auf die unabhängigen Quellen u1 und i2 berechnen. Wie bezeichnet man diesen
allgemeinen Zusammenhang?
b)* Bereiten Sie die Schaltung für eine Knotenspannungsanalyse vor, indem Sie den
Operationsverstärker durch das entsprechende Ersatzschaltbild ersetzen und die stromgesteuerten
Elemente zu spannungsgesteuerten Elementen wandeln. Übernehmen Sie dabei die
Knotennummerierung von Bild 1.
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
3
c)* Geben Sie die Gleichungen der Knotenspannungsanalyse ohne Berücksichtigung des Nullors
an.
1
uk,1
2
uk,2
=
3
uk,3
4
uk,4
Yk
uk
=
iq
d) Führen Sie die zur Berücksichtigung des Nullors notwendigen Schritte durch und geben Sie
das resultierende Gleichungssystem in Matrixschreibweise an.
e)* Bestimmen Sie die Spannung u4 als Funktion von u1 und i2 .
4
Aufgabe 2
Mehrtore, CMOS-Schaltungen
(48 Punkte)
u3
3R
3R
u2
u1
Logik
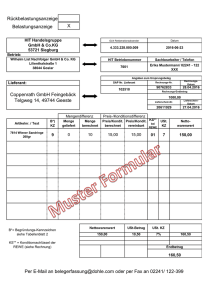
In einem bidirektionalen Bussystem für die Übertragung binärer Daten stören sich, aufgrund der
Imperfektionen des Isolationsmaterials, die Leitungen in beiden Richtungen gegenseitig. Der
nicht-ideale Isolator ist durch Querwiderstände modelliert (siehe Bild 2). Alle Spannungsquellen
nehmen entweder den Wert 0V (≡ logisch ’0’) oder 5V (≡ logisch ’1’) an. In Teil I, wird der
Datenbus als beschaltetes Mehrtor untersucht. In Teil II, soll ein spezieller CMOS-Inverter mit
zwei durch ust gesteuerten Inverterschwellspannungen analysiert werden, der für die
Rekonstruktion der binären Quelle u eingesetzt wird. In Teil III, wird die Logik zur Ansteuerung
des Inverters entworfen.
3R
R
u
Datenbus
ue
0A
Inverter
ua
ust
Bild 2. Zu untersuchende Schaltung
Beachte: Die folgenden drei Aufgabenteile können unabhängig voneinander gelöst werden.
Teil I: Analyse des Datenbusses
In diesem Teil, soll die Störung auf einer bestimmten Leitung (Strecke von u zu ue ) untersucht
werden. Dabei stellen drei andere Leitungen, die durch die Spannungsquellen u1 , u2 und u3
angesteuert sind, die Störquellen dar.
a)* Geben Sie ue als Funktion von u für u1 = u2 = u3 = 0V an.
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
5
b)* Geben Sie ue als Funktion von u1 für u = u2 = u3 = 0V an.
c) Geben Sie nun ue als Funktion von u, u1 , u2 , und u3 an. Nutzen Sie hierfür die Ergebnisse aus
den Teilaufgaben a) und b) sowie das Superpositionsprinzip.
d) Welchen Wert kann die Spannung ue maximal annehmen, wenn u = 0V? Und welchen Wert
kann ue minimal annehmen, wenn u = 5V?
Hinweis: Zur Erinnerung u1 , u2 , u3 ∈ {0V, 5V}.
6
Teil II: Steuerbarer CMOS-Inverter
Aus dem vorherigen Teil geht hervor, dass die binäre Spannung u sich nicht mit einem üblichen
CMOS-Inverter alleine aus der Spannung u rekonstruieren lässt. Bild 3 zeigt einen speziellen
Inverter mit dem Eingang ue und dem Ausgang ua . Durch die Steuerspannung ust soll zwischen
zwei möglichen Inverterschwellspannungen umgeschaltet werden. Die Inverterschwellspannung
ist die Eingangsspannung, bei der der Übergang zwischen ’1’ und ’0’ am Ausgang stattfindet
(nicht zu verwechseln mit den Transistorschwellspannungen Uth = ±1V). Für die Drainströme
der Transistoren im Sättigungsbereich, gilt
id,i =
βi
(ugs,i − 1V)2 mit uds,i ≥ ugs,i − 1V ≥ 0 für i ∈ {1, 3, 5},
2
und
id,i = −
βi
(ugs,i + 1V)2 mit uds,i ≤ ugs,i + 1V ≤ 0 für i ∈ {2, 4, 6}.
2
Außerdem, gilt β3 = β4 = 3β1 = 3β2 . Hingegen sind β5 und β6 so groß, dass die Transistoren
T5 und T6 als Schalter (Leerlauf/Kurzschluss je nach Spannung ust ) betrachtet werden können.
T6
T2
T4
ust
T3
T1
ue
T5
ua
5V
Bild 3. CMOS-Inverter mit schaltbarer Inverterschwellspannung
e)* Vereinfachen Sie die Schaltung aus Bild 3 soweit wie möglich für den Fall ust = 0V. Folglich
wird die Drain-Source-Strecke von T5 als Leerlauf und die Drain-Source-Strecke von T6 als
Kurzschluss betrachtet.
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
f) Bestimmen Sie die erste Inverterschwellspannung ue = Ue,1 zahlenmässig für den Fall
ust = 0V. Hierzu befinden sich die Transistoren T1, T2 und T4 im Sättigungsbereich.
g) Geben Sie für den Fall aus Teilaufgabe f) den Bereich für die Ausgangsspannung ua so an,
dass sich die Transistoren T1, T2 und T4 tatsächlich im Sättigungsbereich befinden.
7
8
h) Skizzieren Sie, ausgehend von Ihren bisherigen Ergebnissen, den Verlauf der Kennlinie des
Inverters für den Fall ust = 0V.
ua
5V
0
5V
ue
i)* Vereinfachen Sie nun die Schaltung aus Bild 3 soweit wie möglich für ust = 5V. Somit wird
die Drain-Source-Strecke von T5 als Kurzschluss und diejenige von T6 als Leerlauf betrachtet.
j) Bestimmen Sie die zweite Inverterschwellspannung ue = Ue,2 zahlenmässig. Nehmen Sie
dabei an, dass sich die Transistoren T1, T2 und T3 im Sättigungsbereich befinden.
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
k) Geben Sie für den Fall aus Teilaufgabe j) den Bereich für die Ausgangsspannung ua so an,
dass sich die Transistoren T1, T2 und T3 tatsächlich im Sättigungsbereich befinden.
l) Skizzieren nun Sie den Verlauf der Kennlinie des Inverters für den Fall ust = 5V.
5V
0
ua
5V
ue
9
10
Teil III: Logikschaltung
Für die Generierung der Steuerspannung ust geht man von folgender Überlegung aus. Falls
mindestens zwei der drei Spannungen, u1 , u2 und u3 , 5V sind, dann begünstigt ihre Interferenz
auf die Spannung ue den Wert ’logisch 1’, und deshalb steuert man die obere
Inverterschwellspannung. Umgekehrt, wählt man die untere Inverterschwellspannung dann, wenn
mindestens zwei der drei Spannungen 0V sind. Die nachgeschaltete Logik trifft also ausgehend
von u1 , u2 und u3 eine Mehrheitsentscheidung.
m)* Geben Sie den Booleschen Ausdruck einer Mehrheitsentscheidungsfunktion f (u1 , u2 , u3 ) an,
die den Wert ’1’ annimmt wenn mindestens zwei der drei Argumente ’1’ sind.
Die optimale Booleschen Funktion für die Steuerspannung ust ergibt sich zu
ust = (u1 ∨ (u2 ∧ u3 )) ∧ (u2 ∨ u3 ).
n)* Zeichnen Sie eine Logikschaltung auf Transistor-Ebene in CMOS-Technologie, die die
Funktion ust als Komplex-Gatter realisiert.
u3
u2
PU
ust
u1
5V
PD
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Aufgabe 3
Bipolare Transistoren
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
11
(19 Punkte)
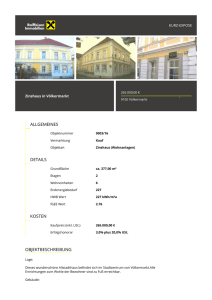
Gegeben sei das folgende Eintor, bestehend aus einem npn-Transistor, einem Widerstand, einem
idealen Übertrager und einer Spannungsquelle.
F
i1
ü:1
i2
u
u2
u1
i
R
ic
ib
U0
ube
Bild 4: Transistor-Schaltung
Die Spannungsquelle U0 > 0 ist konstant. Es wird angenommen, dass der Transistor sich im
Vorwärtsbetrieb befindet. Somit gelte:
ube
ib = Is (e UT − 1)
ic = βib ,
mit der Stromverstärkung β. Für den idealen Übertrager gilt u1 = ü · u2 und i1 = −i2 /ü.
i
.
a)* Zeigen Sie, dass ib = − β+ü
12
b)* Bestimmen Sie allgemein die Widerstandsbeschreibung des Eintors u = r(i) für allgemeine
Bauelementwerte.
Nun folgt eine Kleinsignal-Analyse. Für den Transistor soll das Kleinsignal-Ersatzschaltbild aus
Bild 5 verwendet werden.
β∆ib
∆ib
b
c
r
e
Bild 5: Transistor KS-ESB
c)* Zeichnen Sie das KS-Ersatzschaltbild des Eintors, indem Sie die Ersatzschaltung aus Bild 5
für den Transistor einsetzen und die konstanten Quellen durch Nullquellen ersetzen.
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d) Leiten Sie den Kleinsignalwiderstand rF =
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
∆u
∆i
her.
e) Was muss das Übertragungsverhältnis ü bei gegebener Stromverstärkung β erfüllen, damit
rF < 0 ist? Hinweis: β, R, r > 0.
13
14
90