Parabel und ihr Brennpunkt - PD Dr. rer. nat. habil. Gert Hillebrandt

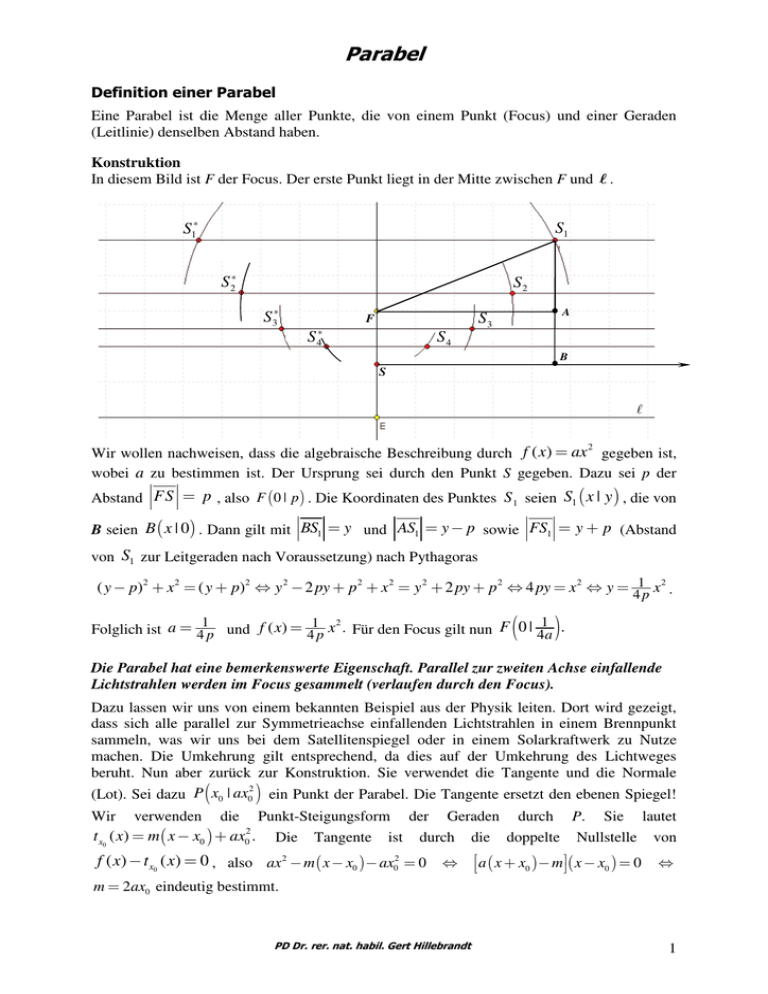
Parabel
Definition einer Parabel
Eine Parabel ist die Menge aller Punkte, die von einem Punkt (Focus) und einer Geraden
(Leitlinie) denselben Abstand haben.
Konstruktion
In diesem Bild ist F der Focus. Der erste Punkt liegt in der Mitte zwischen F und ℓ .
S1∗
S1
S 2∗
S2
S3∗
•A
S3
F
S 4∗
S4
•
S
B
ℓ
2
Wir wollen nachweisen, dass die algebraische Beschreibung durch f ( x ) = ax gegeben ist,
wobei a zu bestimmen ist. Der Ursprung sei durch den Punkt S gegeben. Dazu sei p der
Abstand FS = p , also F (0 | p ) . Die Koordinaten des Punktes S 1 seien S1 ( x | y ) , die von
B seien B ( x | 0) . Dann gilt mit BS1 = y und AS1 = y − p sowie FS1 = y + p (Abstand
von S1 zur Leitgeraden nach Voraussetzung) nach Pythagoras
( y − p)2 + x2 = ( y + p)2 ⇔ y 2 − 2 py + p 2 + x2 = y 2 + 2 py + p 2 ⇔ 4 py = x2 ⇔ y = 41p x2 .
(
)
2
Folglich ist a = 41p und f ( x) = 41p x . Für den Focus gilt nun F 0 | 41a .
Die Parabel hat eine bemerkenswerte Eigenschaft. Parallel zur zweiten Achse einfallende
Lichtstrahlen werden im Focus gesammelt (verlaufen durch den Focus).
Dazu lassen wir uns von einem bekannten Beispiel aus der Physik leiten. Dort wird gezeigt,
dass sich alle parallel zur Symmetrieachse einfallenden Lichtstrahlen in einem Brennpunkt
sammeln, was wir uns bei dem Satellitenspiegel oder in einem Solarkraftwerk zu Nutze
machen. Die Umkehrung gilt entsprechend, da dies auf der Umkehrung des Lichtweges
beruht. Nun aber zurück zur Konstruktion. Sie verwendet die Tangente und die Normale
2
(Lot). Sei dazu P ( x0 | ax0 ) ein Punkt der Parabel. Die Tangente ersetzt den ebenen Spiegel!
Wir
verwenden
die
Punkt-Steigungsform der Geraden durch P. Sie lautet
t x0 ( x) = m ( x − x0 ) + ax . Die Tangente ist durch die doppelte Nullstelle von
2
0
f ( x) − t x0 ( x) = 0 , also ax 2 − m ( x − x0 ) − ax02 = 0 ⇔
 a ( x + x0 ) − m ( x − x0 ) = 0


⇔
m = 2ax0 eindeutig bestimmt.
PD Dr. rer. nat. habil. Gert Hillebrandt
1
Parabel
Folglich ist
t x0 ( x) = 2ax0 ( x − x0 ) + ax02
1
n x0 ( x ) = − 2 ax
0
und die Normale, hier das Lot, somit
( x − x 0 ) + ax 02 .
Tangente
β
T
α
Lot
B
N
β
T*
Aufgrund des Reflexionsgesetzes sind Einfalls- und Reflexionswinkel gleich. Deshalb gilt
2
auch α = β . Die Tangente t x0 ( x) = 2ax0 x − ax0 schließt folglich mit der 2. Achse denselben
Winkel ein wie mit dem einfallenden Strahl (Stufenwinkel). Das Dreieck △TBT * ist folglich
1
gleichschenklig. Der Schnittpunkt der Tangente mit der ersten Achse ist N 2 x0 | 0 . Dies
2
folgt sofort aus 0 = t x0 ( x) = 2ax0 x − ax0 . Damit ist N als der Mittelpunkt der Basis des
(
)
∗
*
Dreiecks △TBT erkannt, da die Dreiecke kongruent sind. Die Höhe auf der Seite TT Ist
folglich parallel zum Lot. Der Fokus berechnet sich daher mittels der parallelverschobenen
(
)
1 x − 1 x . Sie schneidet die zweite
Normalen (Lot) durch N. Folglich ist n1 ( x) = − 2ax
2 0
0
(
)
(
)
1 0 − 1 x = 1 . Dies ist der Brennpunkt B 0 | 1 . Damit ist schon
Achse in n1 (0) = − 2 ax
2 0
4a
4a
0
alles gezeigt.
Der Reflexionsstrahl wird beschrieben durch
r ( x) =
2 2
ax02 − 1
4a x + 1 = 4 a x0 − 1 x + 1 = 1  4a 2 x 2 − 1 x + 1
0
x0
x0

4a
4a
4a 
4 ax0
(
)
oder durch
r ( x) =
2 2
ax02 − 1
4a ( x − x ) + ax 2 = 4a x0 − 1 ( x − x ) + ax 2 .
0
0
0
0
x0
4ax0
2
2 2
Setzen wir r ( x ) = y , so folgt auch 4 ax0 ( y − ax 0 ) − (4 a x 0 − 1)( x − x 0 ) = 0 .
PD Dr. rer. nat. habil. Gert Hillebrandt
2