m - AIA RWTH
Werbung
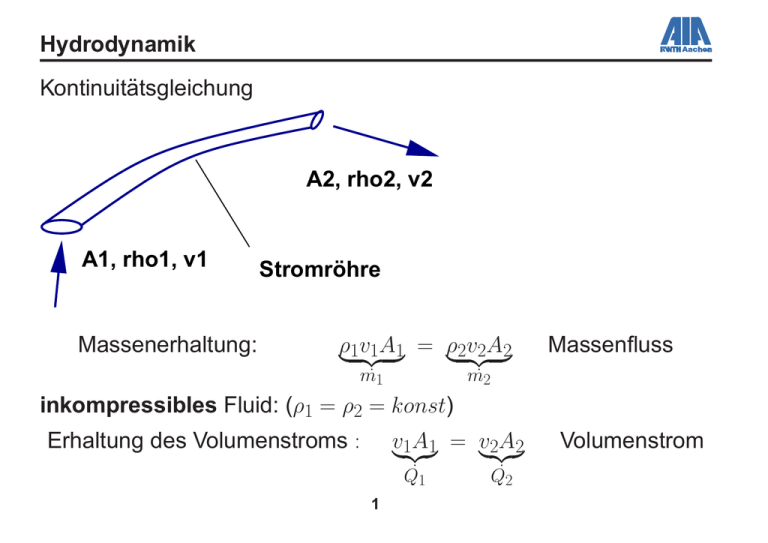
Hydrodynamik
Kontinuitätsgleichung
A2, rho2, v2
A1, rho1, v1
Massenerhaltung:
Stromröhre
ρ
2A}2
1A}1 = ρ
| 2v{z
| 1v{z
ṁ1
Massenfluss
ṁ2
inkompressibles Fluid: (ρ1 = ρ2 = konst)
Erhaltung des Volumenstroms :
v|1{z
A}1 = v|2{z
A}2
Q̇1
1
Q̇2
Volumenstrom
Hydrodynamik
Beispiel
Rohrströmung: A = konst
geschlossene Stromröhre
Wasserstrahl
m
m
1111111111
0000000000
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
1
m
2
geschlossenes Kontrollvolumen
ṁ1 = ṁ2 + ṁ3
3
2
Kontinuität
WICHTIG: In der 1-dimensionalen Kontinuitätsgleichung ist ~v
ein Mittelwert der Geschwindigkeit. In Wirklichkeit ist ~v nicht
konstant wegen Reibungseffekten, Wirbeln, . . .!
h
y
x
~v ist konstant
in der Kontinuitätsgleichung
Realität
~v = ~v (y)
Der Massenstrom muß der ZGleiche sein
−→
ρv(y) dy = ρv̄h
3
Bernoulli
2.Newton’sches Gesetz:
Masse × Beschleunigung = Summe der äußeren Kräfte
d~v X
m·
=
Fa
dt
Bewegungsgleichung für ein infinitesimales Element entlang einer
Stromlinie
g
z
Druck
Reibung
∂p
dz
d~v
= −
− ρg
− R‘
ρ
dt
∂s
ds
s
Trägheit
4
Gravitation
Bernoulli
entlang einer Stromlinie: v = v(s, t)
∂~v
∂~v
d~v =
dt +
ds
∂t
∂s
d~v
∂~v
ds ∂~v
∂~v
∂~v
−→
=
+
=
+ v
dt
∂t
dt ∂s ∂t
∂s
totale
(substantielle)
Beschleunigung
eines Partikels
lokale Beschleunigung
konvektive Beschleunigung
5
Beispiel
Rohrströmung
Diffusor
A
v(x)
ρ
v1(t)
v0 = konst
v2(t)
A, ρ = konst
−→ v1(t) = v2(t)
nur lokale Beschleunigung
nur konvektive Beschleunigung
6
Beispiel
Annahmen:
• inkompressibel (ρ = konst)
• reibungsfrei (R‘ = 0)
∂ =0
• stationär ∂t
• konstante Gravitation (~g = konst)
h
i
∂v = − ∂p − ρg dz −R‘
ρ ∂v
+
v
∂t
∂s
∂s
ds
=0
=0
∂ = d
f (s) −→ ∂s
ds
1 dv 2
dp
dz
ρ 2
ρ
= −
− ρg −→ v + p + ρgz = konst
2 ds
ds
ds
2
7
Druckmessung
statischer Druck: p (Index: 1, 2, a, ∞)
1111111
0000000
p
1
1111111
0000000
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
0000000
1111111
p
111111
000000
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
111111
Totaldruck (Pitotrohr): p0, p01, p02, pt
p0 = p + 12 ρv 2 + ρgh
bei konstanter Höhe ∆h = 0
−→ p0 = p + 12 ρv 2
8
Druckmessung
Potentialdruck: ppot = ρgh
h
1111111111111111111
0000000000000000000
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
dynamischer Druck: pdyn = 12 ρv 2
die kinetische Energie wird umgewandelt, wenn die Strömung auf
~v = 0 verzögert wird
9
6.4
Aus einem großen Überdruckbehälter strömt Wasser ins Freie. Zwischen den Querschnitten A1 und A2 wird die Druckdifferenz ∆p gemessen.
A1 = 0, 3 m2,
A2 = 0, 1 m2,
h = 1 m,
A3 = 0, 2 m2,
ρ = 103 kg/m3,
pa = 105 N/m2,
∆p = 0, 64 · 105 N/m2
g = 10 m/s2
Bestimmen Sie
a) die Geschwindigkeiten v1, v2, v3,
b) die Drücke p1, p2, p3 und den Druck p über dem Wasserspiegel!
10
6.4
Druckbehälter mit Düse
pB
z
h = konst.
gut gerundeter Einlass
1
2
3
Venturidüse
11
6.4
Erhaltung der Gesamtenergie entlang einer Stromlinie (qualitativ)
p
1/2 rho v3**2
1/2 rho v2**2
rho g h
pB
1/2 rho v1**2
p3 = pa
p
1
p2
s
1 2
Bernoulli: p0 = pB + ρgh = pi + ρvi
2
12
6.4
Kontinuität (Massenbilanz): =⇒ = ṁ = ρQ̇ = konst.
ρ = konst =⇒ v1A1 = v2A2 = v3A3 =⇒ A ↓ =⇒ v ↑ =⇒ p ↓
Bernoulli: p1 + ρ2 v12 = p2 + ρ2 v22
ρ 2
=⇒ ∆p = p1 − p2 = (v2 − v12) > 0
2
#
"
v
u2
2
A2 2
m
ρ
∆p
u = 12
→ ∆p =
1 − 2 v2 −→ v2 = u
2
tρ
2
s
A1
A2
1− A
a) gemessen ∆p = p1 − p2
A2
v1 = v2
A1
1
m
A2
=4
v1 = v2
A1
s
A2
m
v3 = v2
=6
A3
s
13
6.4
Die Venturidüse dient zur Massen- und Volumenstrommessung!
Q̇ = vA = v2A2
Prinzip:
• Messung von ∆p
• Berechnung von v2
• Berechnung von Massen- und Volumenstrom
14
6.4
b) Berechnung der Drücke pB , p1, . . . , p3
p0 stellt die Energie dar, die in kinetische Energie umgewandelt werden kann.
ρ 2
ρ 2
ρ 2
p0 = pB + ρgh = p1 + v1 = p2 + v2 = p3 + v3
2
2
2
Wenn ein Druck bekannt ist, können die anderen mithilfe der BernoulliGleichung berechnet werden.
111111111111
000000000000
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
p3 im Austrittsquerschnitt
Annahme: parallele Stromlinien am
scharfkantigen Austritt
15
111111111111
000000000000
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
000000000000
111111111111
Bewegungsgleichung für ein Element
111111111
000000000
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
p(x+dx)dA
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
111111111111111111111111
000000000000000000000000
1
0
1
0
1
0
1
0
x
z
1
0
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000
111
000000000
111111111
000
111
000000000
111111111
g
000
111
000000000
111111111
000
111
000000000
111111111
000
111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000
111
111
000
p(x)dA
Bewegungsgleichung in x-Richtung für ein mitbewegtes Kontrollvolumen
dAdx (enthält immer die gleichen Partikel)
16
Bewegungsgleichung für ein Element
m du
dt = ẍρdAdx = p(x)dA − p(x + dx)dA
∂p
∂p
−→ ẍρdAdx = p(x)dA − p + ∂x
dx dA −→ ρẍ = − ∂x
Annahme: parallele Stromlinien
−→ ẋ = 0
−→
Geschwindigkeit
u = dx
dt = ẋ
∂p
=0
notwendige Bedingung: ẍ = 0 −→ ∂x
=⇒ der Druck im Austrittsquerschnitt ist eine Funktion von y
dp
Strömung in Luft:
= −ρg
dy
Vern. der pot. Energie von Luft −→ pAustritt = pU mgebung = konst.
17
6.4
p3 = pa
Bemerkung:
Bernoulli: 0 −→ 3
pB + ρgh = pa + 12 ρv32
q
−→ v3 = ρ2 (pB − pa + ρgh)
offener Behälter pB = pa
p
−→ v3 = 2gh 6= f (A3)
Theorem von Torricelli (15.Okt. 1608 25.Okt. 1647)
18
erweiterter Bernoulli
rho = const.
A1
A2
v1
v2
Verengung
Delta h ~ Delta p
Theoretischer Volumenstrom: Q̇th für reibungsfreie Strömung
ρ 2
ρ 2
1. Bernoulli: p1 + v1 = p2 + v2
2
2
2. Kontinuität: v1A1 = v2A2
19
erweiterter Bernoulli
A2
Verhältnis der Querschnitte: m =
: −→ Konti v1 = v2m
A1
p1 1 2 2 p2 1 2
+ v2 m = + v2
−→ Bernoulli:
ρ 2
ρ 2
−→
−→
p1 − p2
∆p
2
2
v2 1 − m = 2
=2
ρ
ρ
s
2∆p
v2 =
ρ(1 − m2)
−→ Q̇th = A2
s
2∆p
ρ(1 − m2)
20
erweiterter Bernoulli (Forts.)
In der Realität entstehen Verluste durch Dissipation, Wirbel, . . .
−→ Die Reibung muss berücksichtigt werden.
Die Verluste und die Kontraktion werden in der
Durchflusszahl α zusammengefasst.
Q̇real = αA2
s
2∆p
ρ
α aus Experimenten
Wirbel, Dissipation
Die Strömung in Rohren kann ebenfalls so bestimmt werden.
21
erweiterter Bernoulli (Forts.)
Druckverluste
L · 1 ρv 2
• durch Rohrreibung (Durchmesser D, Länge L): ∆pv = λ D
2
• in Einbauten (Krümmer, Verengung, . . .): ∆pv = ζ · 21 ρv 2
∆pv D
Druckverlust
D
Rohrreibungsbeiwert: λ = 1
· =
·
2
L dynamischer Druck L
2 ρv
∆pv
Druckverlust
=
Verlustbeiwert: ζ = 1
2
dynamischer Druck
2 ρv
22
