- PILOTLINE

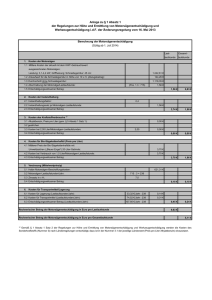
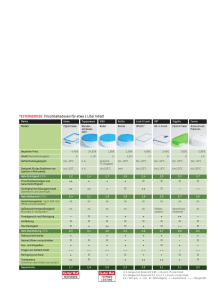
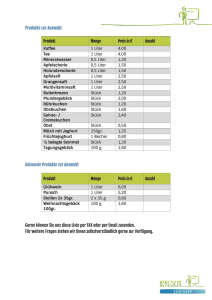
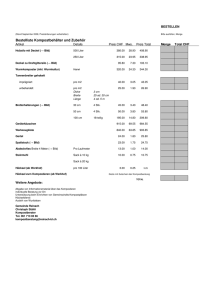
Rechenaufgaben (Dezember 2011)
Auf diesem Dokument werden nochmals die wichtigsten Themen für den Mathematik-Test am SphairScreening erläutert und kurz erklärt.
Proportionaler Dreisatz
Der proportionale Dreisatz besagt: je mehr von Komponente A, desto mehr von Komponente B. Beide
Komponente steigen also gemeinsam und somit proportional.
Beispiel
Für 2 Liter Wein bezahlt man beispielsweise 15.60CHF. Nun stellt sich die Frage, wie viel es kosten
würde, wenn man 4.5 Liter von diesem Wein kaufen würde. Übersichtshalber verwendet man eine
Tabelle.
Anzahl
2 Liter
Preis
15.60CHF
Der Einfachheit halber fragt man sich nun, wie viel 1 Liter kostet. Folglich dividiert man beide Werte mit
2, so dass folgendes resultiert:
Anzahl
2 Liter
1 Liter
Preis
15.60CHF
7.80CHF
Nun weiss man, wie viel 1 Liter Wein kostet. Jetzt kann man für beliebig viele Liter den Preis ermitteln.
Für 4.5 Liter multipliziert man nun beide Seiten mit 4.5, so sieht man, dass 4.5 Liter etwa 35.10CHF
kosten:
Anzahl
2 Liter
1 Liter
4.5 Liter
Preis
15.60CHF
7.80CHF
35.10CHF
Proportionaler Dreisatz bedeutet also nichts anderes, als dass man auf beiden Seiten des typischen
Dreisatzes dieselben Operationen (Multiplikation und Division) verwendet.
PILOTLINE– Rechenaufgaben | 1
Antiproportionaler Dreisatz
Der Antiproportionale Dreisatz ist ähnlich aufgebaut wie der proportionale Dreisatz. Dieser Art von
Dreisatz wird jedoch dann verwendet, wenn die Komponente A steigt, und die Komponente B sinkt!
Beispiel
4 Maurer erstellen eine Wand in einem Tag (die Grösse der Wand spielt dabei keine Rolle). Wenn nun
nur noch ein Maurer dieselbe Wand erstellen soll, so bräuchte er dafür länger.
Würde man nun also den proportionalen Dreisatz verwenden, so würde herauskommen, dass ein
Maurer die gesamte Wand innert 6 Stunden fertiggestellt hätte. Da er aber alleine ist, muss er sämtliche
Arbeiten selber erledigen und benötigt dafür also mehr Zeit. Folglich gilt: je weniger von Komponente A,
desto mehr von Komponente B.
Anzahl
4 Arbeiter
Benötigte Zeit
24 Stunden
Beim antiproportionalen Dreisatz verwendet man auf den beiden Seiten unterschiedliche Operationen,
nämlich jeweils die entsprechende Gegenoperation. So sinkt also die Anzahl Arbeiter (ursprünglich 4
Arbeiter, neu 1 Arbeiter). In diesem Fall steigt aber die benötigte Zeit. Der Wert auf der linken Seite wird
also mit 4 dividiert, derjenige auf der rechten Seite mit dem Wert 4 multipliziert.
Anzahl
4 Arbeiter
1 Arbeiter
Benötigte Zeit
24 Stunden
96 Stunden
Dabei ist deutlich zu erkennen: Komponente A (Anzahl Arbeiter) sinkt, Komponente B (benötigte Zeit)
steigt.
PILOTLINE– Rechenaufgaben | 2
Satz des Pythagoras
Der Satz des Pythagoras dient dazu, eine Seite eines rechtwinkligen Dreiecks auszurechnen, sofern
mindestens zwei Längen des Dreiecks bekannt sind. Der Satz des Pythagoras ist weit verbreitet und
gehört deshalb zu jedem Grundwissen in der Mathematik und Physik.
Grundsätze
Der Satz des Pythagoras gilt nur in einem rechtwinkligen Dreieck. Dabei gibt es die beiden Katheten a
und b, sowie die Hypotenuse mit dem Buchstaben c. Grundsätzlich gilt:
a² + b² = c²
Dieser Grundsatz kann mit den allgemeinen Regeln der Mathematik umgewandelt warden. Daraus
folgen folgende Gleichungen:
c² - a² = b²
c² - b² = a²
Wichtig: Beim Satz des Pythagoras jeweils nicht vergessen, die Werte zu quadrieren. Umgekehrt muss
man die Quadratwurzel des entsprechenden Wertes nehmen, wenn man beispielsweise die Länge der
Strecke c ermitteln will.
Geschwindigkeiten
Oftmals muss eine Geschwindigkeit in eine andere Einheit umgerechnet werden. Beispielsweise muss
man, damit man nicht mit unterschiedlichen Einheiten eine Aufgabe löst, die Einheit m/s (Meter pro
Sekunde) in km/h (Kilometer pro Stunde) umrechnen oder umgekehrt. Dabei gilt folgender, einfacher
Grundsatz:
- Die Anzahl Kilometer pro Stunde (km/h) wird durch 3.6 dividiert, damit man die Anzahl Meter pro
Sekunde erhält.
- Die Anzahl Meter pro Stunde (m/s) wird mit 3.6 multipliziert, damit man die Anzahl Kilometer pro
Stunde erhält.
PILOTLINE– Rechenaufgaben | 3
WICHTIGE HINWEISE
- Das gesamte Dokument darf nicht ohne ausdrückliche Zustimmung des Autors (Webmaster von www.pilotline.ch) verändert
oder weitergegeben werden.
- Dieses Dokument darf nur auf der Seite www.pilotline.ch zum Download angeboten werden.
- Alle Bilder und Texte dürfen unter keinen Umständen kopiert und/oder übernommen werden.
- Alle Angaben sind ohne Gewähr
- Dieses Dokument garantiert keinen positiven Erfolg
Das Dokument ist geschützt:
© 2011 by pilotline.ch
KONTAKTDATEN
[email protected]
www.pilotline.ch
PILOTLINE– Rechenaufgaben | 4