Aufgabe - Positron Annihilation in Halle - Martin-Luther

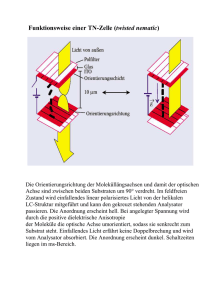
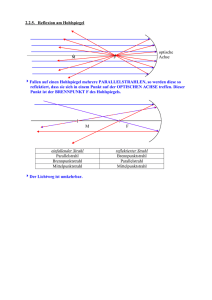
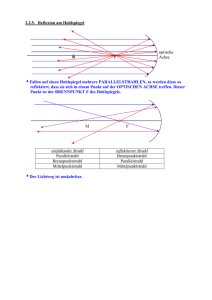
Martin-Luther-Universität
Halle-Wittenberg
FB Physik
FortgeschrittenenPraktikum
Versuch 21: Spannungsoptik
1)
Mit Hilfe der Polarisationsfilter sind die Lagen der optischen Achsen für die beiden λ/4Filter zu bestimmen.
2)
Der Spannungszustand einer eingespannten Piacryl-Probe ist optisch darzustellen.
Variieren Sie den Versuchsaufbau in der folgenden Weise:
-
Drehung des Analysators;
-
Drehung von Polarisator und Analysator gemeinsam, so dass beide zueinander
rechtwinklig orientiert bleiben;
-
Einsetzen der beiden λ/4-Filter zwischen Probe und Analysator bzw. Polarisator so,
dass die optischen Achsen um 45° gegen die Ebene des Polarisators geneigt sind.
Erklären Sie Ihre Beobachtungen. Kennzeichnen Sie Isochromaten und Isoklinen in
der Fotografie!
3)
Man wähle in der mittels monochromatischem Licht gewonnenen Aufnahme einen
Punkt aus (Bedingung: τxy ╪ 0) und ermittle hierfür den ebenen Spannungszustand,
d.h. gebe die Komponenten der Spannung in x- und in y-Richtung an. (Die x-Achse
liege in horizontaler Richtung, also in Richtung der spannungsverursachenden Kraft,
die y-Achse sei vertikal orientiert.)
4)
An der kommerziellen Spannungsoptik-Bank sind die Spannungslinien einer
Glasscheibe bei thermischer Belastung mit der Kamera als Funktion des
Polarisationswinkels aufzunehmen (10°-Schritte 0…90°).
5)
Aus den unter 4) aufgenommenen Fotos ist der Verlauf der Hauptspannungslinien zu
bestimmen. Das Ergebnis ist zu interpretieren.
6)
Führen Sie an dieser Bank den Balkenbiege-Versuch mit einer Piacrylstange durch.
Bringen Sie zusätzlich ein Quarzplättchen in den Strahlengang und interpretieren Sie
die Farberscheinungen (s. Bergmann-Schäfer, Optik).
7)
Testen und fotografieren Sie weitere am Messplatz vorhandene Objekte.
Daten: Spannungsoptische Konstante für Piacryl bei λ=548 nm: so=151,9 MPa⋅mm
(±1,5%); Dicke der Piacryl/Plexiglas-Probe: 5,5 mm
Hinweis: Die Digitalkamera Fuji Finpix S5500 ist mit manueller Fokussierung zu betreiben
(Makromodus benutzen, Belichtung manuell ausprobieren bzw. Nachtprogramm testen).
Literatur:
[1]
Föppl, Mönch: Praktische Spannungsoptik (im Bestand der Handbibliothek des
Praktikums)
[2]
Kuske: Taschenbuch der Spannungsoptik
[3]
Bergmann-Schäfer, Band III: Optik
[4]
Sommerfeld: Mechanik der deformierbaren Medien
[5]
Pohl: Optik
[6]
Grimsehl: Physik III
Kontrollfragen:
1. Wie kann man polarisiertes Licht erzeugen?
2. Was bedeutet „Doppelbrechung“? Was unterscheidet Dichroismus und
Doppelbrechung?
3. Wie kann aus linear polarisiertem Licht zirkular polarisiertes Licht werden? Erklären
Sie die Wirkungsweise eines λ/4-Plättchens.
4. Wie kann man experimentell unpolarisiertes Licht von zirkular polarisiertem Licht
unterscheiden?
5. Erklären Sie, warum nichtkristalline Materialien unter mechanischer Spannung
optisch anisotrop werden können.
6. Leiten Sie den Zusammenhang zwischen optischer Anisotropie Δn und dem
Gangunterschied (Gleichung in Abschnitt 3 dieser Anleitung) her!
7. Erklären Sie, warum eine lokale Kristallisation amorpher durchsichtiger Stoffe (Glas,
Plexiglas) zur Verringerung der Transmission führen kann!
8. Warum sind die Aufhellungserscheinungen einer mechanisch gespannten Probe
zwischen gekreuzten Polarisatoren farbig?
9. Wie kann man die ebenfalls auftretenden dunklen Linien zwischen den hellen
Bereichen erklären?
Anleitung zum Versuch
Inhalt
1. Zusammenfassung
2. Mechanische Spannungen
Drehung des Koordinatensystems und Spannungstensor
Hauptspannungen und Hauptachsen
3. Optische Anisotropie
Grundlagen
Veränderung des Polarisationszustandes des Lichtes
4. Mechanische Spannung und Doppelbrechung
Zusammenhang zwischen Doppelbrechung und Struktur
Doppelbrechung durch mechanische Spannung
5. Experimenteller Nachweis der Spannungsdoppelbrechung
Versuchsaufbau
Erklärung der Beobachtungen
Quantitative Auswertung
6. Anwendung
1. Zusammenfassung
Optisch isotrope Materialien können unter mechanischer Belastung doppelbrechend werden. Dies kann mit polarisiertem Licht untersucht werden: Man weist die durch die Doppelbrechung bewirkte Veränderung des Polarisationszustandes nach. Die mechanische
Spannung ist je nach ihrer Ursache (äußere Kräfte, oder vorangegangene thermische
Behandlung) ortsabhängig und äußert sich in diesem Versuch in vielfältigen Farbmustern. Aus diesen kann man auf die Verteilung der Spannungen in einem Probekörper
schließen. Diese Möglichkeit wird gelegentlich in einem „Spannungsoptik“ genannten
Verfahren zur Untersuchung der Spannungsverteilung in Bauteilen, Werkstücken etc.
angewandt.
2. Mechanische Spannungen
Die in diesem Versuch auftretenden mechanischen Spannungsverteilungen, die quantitativ ausgewertet werden sollen, lassen sich unter den Begriff „ebener Spannungszustand“ einordnen. Das bedeutet, dass nur in einer Ebene – hier in derjenigen, die
senkrecht zum Lichtstrahl liegt – Spannungen auftreten, senkrecht dazu hingegen nicht.
In Ref. [1] ist eine Herleitung der entsprechenden Gleichungen dargestellt. Hier wird
eine etwas andere Darstellungsform des gleichen physikalischen und mathematischen
Zusammenhanges gegeben.
Drehung des Koordinatensystems und Spannungstensor
Wir fassen Schub- und Scherspannungen in einer Matrix zusammen:
⎛ σ x τ xy ⎞
σ=⎜
⎟
⎜τ
⎟
⎝ yx σ y ⎠
(1)
Hier bedeuten σx und σy die Normalspannungen in x- bzw. y-Richtung. τxy (τyx) ist die
Schubspannung in einer Ebene senkrecht zur x- (y-) Achse längs der y- (x-) Achse. Da
die Schubspannungen in senkrecht aufeinander stehenden Flächen gleich sind (τxy = τyx),
ist die Matrix symmetrisch.
Wir prüfen nun, wie sich σ bei einer Drehung des Koordinatensystems und den Winkel α
verhält (neue Achsen: ξ und η). Dies tun wir, indem wir das Transformationsgesetz für
kartesische Koordinaten auf Gl. (1) anwenden, um anschließend das Ergebnis mit den in
[1] hergeleiteten Beziehungen zu vergleichen:
⎛ σ ξξ
⎜
⎜τ
⎝ ηξ
τ ξη ⎞
⎛ cos α
⎟=⎜
⎟
σ ηη ⎠ ⎝ − sin α
sin α ⎞ ⎛ σ x τ xy ⎞ ⎛ cos α
⎟⎜
⎟⎜
cos α ⎠ ⎜⎝ τ yx σ y ⎟⎠ ⎝ sin α
− sin α ⎞
⎟
cos α ⎠
1
⎛
⎞
2
2
τ yx cos 2α + (σ x − σ y ) sin2α ⎟
⎜ σ x cos α + σ y sin α + τ xy sin2α
2
=⎜
⎟
⎜ τ cos 2α + 1 σ − σ sin2α
2
2
σ x sin α + σ y cos α − τ xy sin2α ⎟⎟
(
⎜ yx
y)
2 x
⎝
⎠
(2)
Dies entspricht genau dem in den Gleichungen (2) und (3) in Ref. [1] auf anderem Wege
Hergeleiteten. Es stellt sich also heraus, dass sich diese Matrix beim Übergang von einem Koordinatensystem in ein anderes wie der Ortsvektor transformiert. Damit darf
gesagt werden, dass σ einen Tensor repräsentiert. (Es sei darauf hingewiesen, dass bei
einer Drehung des Koordinatensystems der Tensor nicht geändert wird, sondern nur
seine Koordinatenmatrix!)
Hauptspannungen und Hauptachsen
Aus der Algebra ist bekannt, dass es für jeden Tensor Koordinatensysteme gibt, in denen
er durch eine diagonale Koordinatenmatrix dargestellt wird. Diese Systeme nennt man
Hauptachsensysteme. Ihre Lage widerspiegelt die Symmetrie des jeweiligen Problems.
Die Hauptachsen werden hier als x1- bzw. x2-Achse bezeichnet. Im Falle des ebenen
Spannungszustandes treten die größte bzw. kleinste Normalspannung jeweils längs einer
der beiden Hauptachsen auf und werden als Hauptspannungen σ1 bzw. σ2 bezeichnet.
Die Schubspannungen längs der beiden Achsen sind null.
Da diese Hauptachsensysteme den lokalen Spannungszustand charakterisieren, sind sie
i. allg. von Punkt zu Punkt verschieden (siehe Abb. 1).
y
x2
σ2 σyy
σ1
σxx
x1
x2
σyy σ2
σxx
σ1
x1
x
Abb. 1: Schematische Darstellung des Spannungszustandes zweier Punkte einer
Probe. Die Hauptspannungen sind durch rote bzw. blaue Strecken dargestellt. Die
Normalspannung in einer anderen Richtung entspricht der Strecke vom Ursprung
zur Peripherie der ellipsenähnlichen Kurve. Zusätzlich ist ein mit der Probe verbundenes Koordinatensystem (xy) dargestellt. Die den Normalspannungen in x- und yRichtung entsprechenden Strecken sind grün bzw. orange eingezeichnet.
Wendet man das oben dargestellte Transformationsgesetz auf den Übergang vom Hauptachsensystem in ein um α gedrehtes xy-System an, erhält man die Darstellung der Normal- und Schubspannungen als Funktion der Hauptspannungen:
⎛ σ xx
⎜
⎜τ
⎝ yx
1
⎛
2
2
(σ 1 − σ 2 ) sin2α ⎞⎟
⎜ σ 1 cos α + σ 2 sin α
2
⎟
⎟=⎜
σ yy ⎟⎠ ⎜ 1
⎟
2
2
σ
σ
α
σ
α
σ
α
−
+
sin2
sin
cos
(
)
⎜
⎟
2
1
2
⎝ 2 1
⎠
τ xy ⎞
(3)
Siehe Gleichungen (7) und (8) in Ref. [1]. Die dortige Gleichung (4) hat
σ xx + σ yy = σ 1 + σ 2 zum Analogon, was nichts Anderes als der Satz der Erhaltung der Spur
eines Tensors bei einer unitären Transformation ist.
3. Optische Anisotropie
Grundlagen
Als „optisch anisotrop“ werden Materialien bezeichnet, bei denen Brechungsindex
und/oder Absorptionskoeffizient von der Polarisationsrichtung abhängen. Die erste Eigenschaft wird als Doppelbrechung bezeichnet, die zweite als Dichroismus.
Diese Materialeigenschaften können auch zur Herstellung von polarisiertem Licht
verwendet werden. Die Doppelbrechung wird z.B. im Nicolschen Prisma genutzt,
der Dichroismus in Polarisationsfiltern (z.B. aus Turmalin); siehe Kontrollfrage 1.
Allerdings ist die optische Anisotropie nicht unbedingte Voraussetzung, denn bekanntlich kann man Licht auch durch Reflexion an Grenzflächen zwischen isotropen Medien polarisieren (Brewstersches Gesetz).
Die in spannungsoptischen Experimenten genutzte Doppelbrechung besteht in der
Aufspaltung eines ankommenden Lichtstrahles in zwei Teilstrahlen, die i.allg. in verschiedenen Richtungen weiterlaufen. M.a.W., es existieren zwei verschiedene Brechungsindizes, verursacht durch zwei verschiedene Fortpflanzungsgeschwindigkeiten des
Lichtes in dem doppelbrechenden Medium.
Für die Beschreibung dieses Phänomens führt man eine optische Achse ein. Ein unter
beliebigem Winkel einfallender Lichtstrahl wird so zerlegt, dass eine Komponente parallel zur optischen Achse polarisiert ist und die zweite senkrecht hierzu. Die erste wird
„außerordentlicher Strahl“, die zweite „ordentlicher Strahl“ genannt. Die zugehörigen Brechungsindices sind nao bzw. no; deren Differenz Δn ist ein Maß für die Stärke des
Effektes. Strahlt man Licht in Richtung der optischen Achse ein, bemerkt man keine
Doppelbrechung, weil hier jede Polarisationsebene senkrecht auf der optischen Achse
steht und somit nur der ordentliche Strahl auftritt. Ebenfalls beobachtet man keine Aufspaltung, wenn das Licht senkrecht zur optischen Achse einfällt und dabei entweder
genau parallel oder senkrecht zur optischen Achse polarisiert ist; hier wird das gesamte
einfallende Licht im außerordentlichen bzw. ordentlichen Strahl weiterlaufen.
Anmerkung: Es gibt auch den Fall der zweiachsigen optischen Anisotropie, d.h. zur Beschreibung benötigt man mehr als eine optische Achse. Da dies in unserem Versuch aber
keine Rolle spielt, wird hier darauf nicht weiter eingegangen.
Veränderung des Polarisationszustandes des Lichtes
Wir betrachten einen senkrecht zur optischen Achse einfallenden Strahl, der zudem
gerade so polarisiert ist, dass der Polarisatorwinkel 45° beträgt (unter „Polarisatorwinkel“ wollen wir hier den Winkel zwischen der Polarisationsebene und der optischen
Achse verstehen). Entsprechend dem eben Dargestellten wird dieser Strahl in einen
außerordentlichen und einen ordentlichen Strahl zerlegt, und zwar zu gleichen Teilen
bezüglich der Intensität.
Beide Teilstrahlen breiten sich nunmehr unterschiedlich schnell aus, was zu einer
stetig anwachsenden Phasendifferenz und damit zu einem Gangunterschied zwischen ihnen führt:
G=d
Δn
nao
(4)
(Siehe Kontrollfrage 6.) Wenn die Dicke der durchstrahlten Schicht gerade so ist, dass
der Gangunterschied λ/4 beträgt, liegt zirkular polarisiertes Licht vor (λ/4Plättchen). Bei λ/2 ergibt sich wieder eine linear polarisierte Welle, deren Polarisationsebene gegenüber der des ursprünglichen Strahles um 90° gedreht ist. (Siehe Kontrollfrage 3.) Dazwischen liegende Schichtdicken erzeugen elliptisch polarisiertes Licht.
Nimmt der Polarisatorwinkel andere Werte als die eben verwendeten 45° an, erfolgt die
Aufteilung der Intensitäten auf ordentlichen/außerordentlichen Strahl nicht mehr im
gleichen Verhältnis der Intensitäten. Nach einem Gangunterschied von λ/2 liegt dann
linear polarisiertes Licht vor, dessen Ebene um einen von 90° verschiedenen Winkel
gegenüber der ursprünglichen Richtung gedreht ist. Auch gibt es bei λ/4 keine zirkulare
Polarisation; alle Zwischenpolarisationen sind elliptischer Art.
In allen Fällen liegt nach Durchlaufen einer Schicht, die einen Gangunterschied von λ
erzeugt, wieder der ursprüngliche Zustand vor.
4. Mechanische Spannung und Doppelbrechung
Zusammenhang zwischen Doppelbrechung und Struktur
In jedem Falle muss ein Material eine anisotrope Struktur besitzen, wenn es doppelbrechend ist. Die makroskopische Größe „Brechungsindex“ ist über die relative Dielektrizitätskonstante ε mit der mikroskopischen Größe „Polarisierbarkeit“ (α) verbunden:
n≈ ε
;
ε − 1 3ε 0 M mol
⋅
=α
ε + 2 NA ρ
(5)
(CLAUSIUS-MOSOTTI-Gleichung; Mmol Molmasse, ρ Dichte, NA Avogadrozahl; nichtferromagnetische Substanz, also µ ≈ 1, angenommen.)
Nun können mehrere Fälle unterschieden werden:
1. Isotrope Polarisierbarkeit, z.B. bei kleinen kugelförmigen Molekülen oder Kristallgitter mit hoher Symmetrie (z.B. kubisch). Dann ist zu erwarten, dass auch n isotrop
ist.
2. Anisotrope Polarisierbarkeit im Einkristall: Hier muss die Symmetrie hinreichend niedrig sein. Beispiel: Kalkspat besitzt einen rhomboedrischen Kristallaufbau.
Die optische Achse liegt in Richtung einer der Raumdiagonalen des Rhomboeders.
3. Anisotrope Polarisierbarkeit; ungeordneter übermolekularer Aufbau: Flüssigkeiten und nichtkristalline feste Materialien (z.B. Glas, manche Polymere) sind normalerweise infolge der Unordnung im molekularen Aufbau optisch isotrop. Alle möglichen Ausrichtungen von Molekülen oder Molekülabschnitten kommen in der gesamten Probe mit gleicher Häufigkeit vor. So gibt es keinen Anlass dafür, dass der Brechungsindex für eine bestimmte Polarisationsrichtung einen anderen Wert haben
könnte als für eine andere.
4. Anisotrope Polarisierbarkeit; teilweise geordneter übermolekularer Aufbau:
Beispiel Flüssigkristalle oder orientierte Polymere (gestreckt, versponnen). Je besser
die Ordnung ist, desto größer ist die Doppelbrechung Δn zu erwarten
5. Optische Isotropie wie Fall 1. oder 3., aber zusätzlich Überlagerung von α mit einer
anisotropen Komponente, die durch mechanische Belastung entsteht. Da die Ursa-
che makroskopischen Ursprungs ist, hat diese Zusatzkomponente eine makroskopische Ausrichtung und führt zu einer beobachtbaren optischen Anisotropie! Das ist die
hier behandelte Spannungsdoppelbrechung; siehe nächster Abschnitt.
Doppelbrechung durch mechanische Spannung
Man beobachtet Doppelbrechung, die proportional zur Differenz der Hauptspannungen
ist: Δn = C (σ 1 − σ 2 ) . Als optische Achse fungiert dabei eine der Hauptachsen des Spannungstensors. Senkrecht zu der ebenen Probe einfallendes polarisiertes Licht wird in
zwei Komponenten, die parallel zu x1 und x2 polarisiert sind, zerlegt. Durchläuft das Licht
eine Schicht der Dicke d, führt dies entsprechend Gl. (4) zu einem Gangunterschied von
g =
d
⋅ (σ 1 − σ 2 )
s0
(6)
(Hauptgleichung der Spannungsoptik)
s0 ist dabei die spannungsoptische Konstante des Materials; g ist der relative Gangunterschied (d.h. auf die Wellenlänge bezogen, also g = G / λ ).
Das Spannungsfeld einer Probe ist i. allg. inhomogen, d.h. die Differenz der Hauptspannungen und die Richtungen der Hauptachsen variieren von Ort zu Ort. Damit sind auch
die optische Anisotropie sowie der Winkel zwischen Polarisationsebene und optischer
Achse ortsabhängig. Dies wiederum resultiert in einer Ortsabhängigkeit des Gangunterschiedes und des relativen Anteils von ordentlichem und außerordentlichem Strahl. Dies
erklärt die beobachteten Farbmuster, wenn sich die Probe zwischen zwei Polarisationsfiltern befindet. Diese Muster können genutzt werden, um lokale Spannungszustände zu
untersuchen; siehe dazu mehr im nächsten Abschnitt.
5. Experimenteller Nachweis der Spannungsdoppelbrechung
Versuchsaufbau
Ggf. λ/4-Filter
Lichtquelle
Polarisator
Probe
Analysator
Schirm
Hierzu bringt man die Probe zwischen zwei gekreuzte Polarisationsfilter, d.h. Polarisationsfilter, deren Richtungen zueinander im rechten Winkel stehen. Wenn die Probe
optisch isotrop ist, kann kein Licht durch diese Anordnung gelangen. Schon geringfügige
Anisotropien, die elliptisch polarisiertes Licht erzeugen, führen jedoch zu einer Aufhellung des Gesichtsfeldes, weil nunmehr das aus der Probe herauskommende Licht auch
eine Komponente parallel zur Durchlassrichtung des Analysatorfilters hat.
Man beobachtet Farbmuster, auf der Titelseite dieser Anleitung ist rechts oben ein
Beispiel zu finden. In Abhängigkeit von Richtung und Stärke der lokalen Spannung beobachtet man unterschiedliche Farben (siehe Kontrollfrage 8).
Dreht man Polarisator und Analysator gemeinsam so, dass beide zueinander gekreuzt bleiben, bemerkt man, dass sich bestimmte dunkle Flächen bewegen, andere
aber nicht. Erstere sind die Isoklinen (s.u.).
Bringt man λ/4-Filter wie in der Skizze angegeben in den Strahlengang (wobei die
Achse des ersten um 45° gegen die Polarisatorrichtung gedreht sein soll), erscheinen
einige bislang dunkle Flächen hell. Wiederum handelt es sich dabei um die Isoklinen.
Die beiden eben dargestellten Zusatzexperimente dienen der Unterscheidung von Isoklinen und Isochromaten. Das wiederum ist für die quantitative Analyse von Bedeutung (s.
unten).
Erklärung der Beobachtungen
Dazu betrachten wir zunächst ein Experiment mit monochromatischem Licht. Die oben
bereits erklärten Aufhellungen werden durch dunkle Stellen umgeben bzw. voneinander
getrennt. Dies ist ein Anzeichen dafür, dass das an bestimmten Stellen der Probe austretende Licht den Analysator nicht passieren kann, weil es wie das in die Probe eintretende Licht polarisiert ist.
Hierfür sind vier verschiedene Ursachen denkbar:
1. Isochromaten: Der Gangunterschied beträgt gerade nλ (siehe oben).
2. Isoklinen: Die Polarisationsebene des einfallenden Lichtes liegt so, dass sie eine
der Hauptspannungsrichtungen, also auch die optische Achse, enthält. Damit liegt in
der Probe nur der ordentliche oder nur der außerordentliche Strahl vor, und es tritt
keine Veränderung des Polarisationszustandes auf.
3. Isotroper Punkt: Die Spannungshauptwerte sind gleichgroß (isotrope Kompression). Dadurch kommt keine Anisotropie zustande; Gl. (6) liefert null für den Gangunterschied.
4. Überhaupt keine Spannung vorhanden.
Bei der eingespannten Piacryl-Probe (Aufgaben 2 und 3) treten die Fälle 1, 2 und 4 auf,
bei der ungleichmäßig erwärmten Glasplatte (Aufgaben 4 und 5) Fälle 2, 3 und 4.
Aus dieser Auflistung wird klar, warum nur die Isoklinen auf die im vorigen Abschnitt
erwähnte Polarisator-Analysator-Drehung reagieren, denn nur sie hängen von der Richtung der Polarisationsebene ab.
Das letzte Zusatzexperiment des vorigen Abschnitts – der Einbau von λ/4-Filtern - nutzt
zirkulare Polarisation. Diese weist überhaupt keine Vorzugsrichtung auf, so dass Isoklinen nicht entstehen können.
Quantitative Auswertung
Hierfür wird die entsprechend dem vorvorigen Abschnitt experimentell durchgeführte
Unterscheidung Isochromaten – Isoklinen benötigt, weiterhin ggf. eine Serie von Aufnahmen, die bei unterschiedlichen Polarisatorwinkeln erzeugt worden sind. Während die
Isochromaten die Information über den Absolutbetrag von σ1 – σ2 enthalten, geben
die Isoklinen Auskunft über die Richtung der Hauptachsen.
Spannungsverhältnisse an einem Punkt: Aus Isochromate
Das Vorgehen zur vollständigen Ermittlung des Spannungsfeldes ist in [1] sehr gut beschrieben. In Kurzfassung:
Ermittlung des Spannungsfeldes: Aufnahme unter verschiedenen Winkeln zwischen Pola-
risator und Probe; Einzeichnen der Isoklinen, daran kurze Striche, de die Richtung angeben; Verfahren nach [1]
6. Anwendung
Mit spannungsoptischen Untersuchungen werden in der Technik an Modellen aus durchsichtigem Material (Epoxidharz, Polyesterharz) Größe und Richtung von Spannungen in
verschiedenen Konstruktionsteilen festgestellt. Dazu fertigt man ein Modell des betreffenden Teiles (Zahnrad, Träger, Brückenbogen...) an und kann dies anschließend im
Strahlengang belasten. Alternativ dazu wird auf das erwärmte Teil außerhalb des Strahlenganges eine entsprechende Belastung ausgeübt und das Material währenddessen
abgekühlt. Die Spannungen werden dabei „eingefroren“, so dass man anschließend im
optischen Gerät frei von zusätzlicher Mechanik arbeiten kann.