3 Scheitelpunktgleichung bestimmen (aus Graphen)

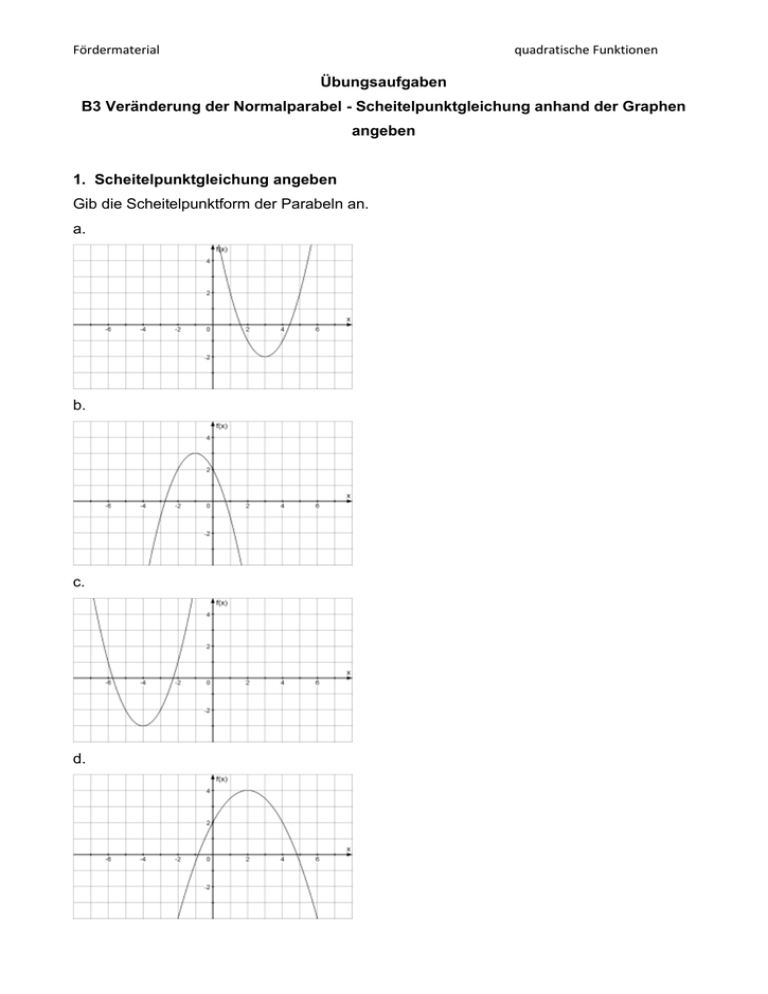
Fördermaterial
quadratische Funktionen
Übungsaufgaben
B3 Veränderung der Normalparabel - Scheitelpunktgleichung anhand der Graphen
angeben
1. Scheitelpunktgleichung angeben
Gib die Scheitelpunktform der Parabeln an.
a.
b.
c.
d.
Fördermaterial
quadratische Funktionen
2. Scheitelpunktgleichung angeben
Gib die Funktionsgleichungen der vier Parabeln an:
Parabel 2
Fördermaterial
quadratische Funktionen
Informationen
B3 Veränderung der Normalparabel - Scheitelpunktgleichung anhand der Graphen
angeben
Scheitelpunktform: f ( x )  a  ( x  d) 2  e
Beispiel:
Liegt der Scheitel bei S(3/-1), so folgt:
f ( x )  ( x  3) 2  ( 1)
f ( x )  ( x  3)2  1
Fördermaterial
quadratische Funktionen
Lösungen
B3 Veränderung der Normalparabel - Scheitelpunktgleichung anhand der Graphen
angeben
1. Scheitelpunktgleichung angeben
a. f ( x )  ( x  3)2  2
b. f ( x )  ( x  1)2  3
c. f ( x )  ( x  4)2  3
d. f ( x )  0,5  ( x  2)2  4
2. Scheitelpunktgleichung angeben
oben:
Parabel 1 y  ( x  4) 2  5
Parabel 2 y  ( x  1,5) 2  3
unten:
Parabel 1 y  ( x  3) 2  5
Parabel 2 y  0,5( x  2,5) 2  3