Kompetenzplan Klassen 5/6
Werbung
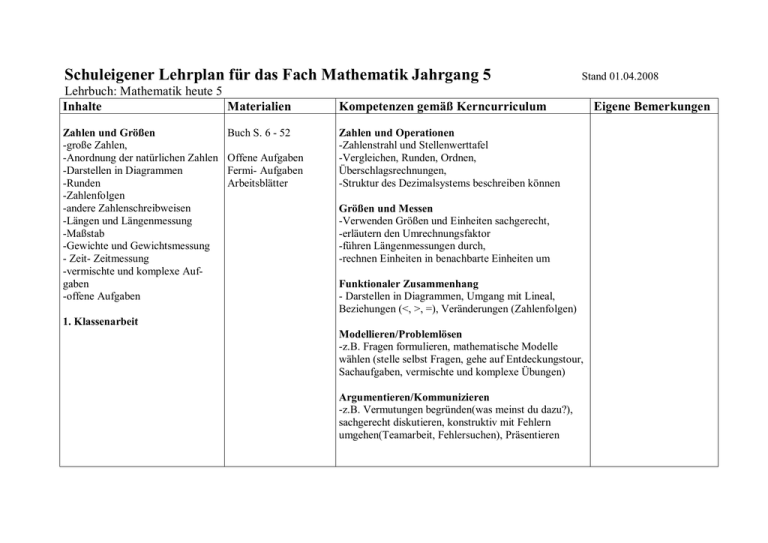
Schuleigener Lehrplan für das Fach Mathematik Jahrgang 5 Lehrbuch: Mathematik heute 5 Inhalte Materialien Zahlen und Größen -große Zahlen, -Anordnung der natürlichen Zahlen -Darstellen in Diagrammen -Runden -Zahlenfolgen -andere Zahlenschreibweisen -Längen und Längenmessung -Maßstab -Gewichte und Gewichtsmessung - Zeit- Zeitmessung -vermischte und komplexe Aufgaben -offene Aufgaben Buch S. 6 - 52 Offene Aufgaben Fermi- Aufgaben Arbeitsblätter Stand 01.04.2008 Kompetenzen gemäß Kerncurriculum Zahlen und Operationen -Zahlenstrahl und Stellenwerttafel -Vergleichen, Runden, Ordnen, Überschlagsrechnungen, -Struktur des Dezimalsystems beschreiben können Größen und Messen -Verwenden Größen und Einheiten sachgerecht, -erläutern den Umrechnungsfaktor -führen Längenmessungen durch, -rechnen Einheiten in benachbarte Einheiten um Funktionaler Zusammenhang - Darstellen in Diagrammen, Umgang mit Lineal, Beziehungen (<, >, =), Veränderungen (Zahlenfolgen) 1. Klassenarbeit Modellieren/Problemlösen -z.B. Fragen formulieren, mathematische Modelle wählen (stelle selbst Fragen, gehe auf Entdeckungstour, Sachaufgaben, vermischte und komplexe Übungen) Argumentieren/Kommunizieren -z.B. Vermutungen begründen(was meinst du dazu?), sachgerecht diskutieren, konstruktiv mit Fehlern umgehen(Teamarbeit, Fehlersuchen), Präsentieren Eigene Bemerkungen Rechnen mit natürlichen Zahlen und Größen -Addieren und Subtrahieren -Multiplizieren und Dividieren -vermischte Übungen zu allen Rechenarten -Terme- Vorrangregeln -Rechengesetze - vorteilhaft rechnen -Lösen von Gleichungen -Potenzieren - Teiler und Vielfache -Teilbarkeitsregeln - Primzahlen, Primfaktorenzerlegung, -vermischte und komplexe Übungen -offene Aufgaben Buch S. 54 - 105 Offene Aufgaben Arbeitsblätter Fermiaufgaben 3. Klassenarbeit Funktionaler Zusammenhang -erkennen und verwenden Variablen als Platzhalter für bestimmte Zahlen und Zahlenmengen Modellieren/Problemlösen -z.B. Fragen formulieren, mathematische Modelle wählen ( Stelle selbst Fragen, gehe auf Entdeckungsreise, Sachaufgaben, vermischte und komplexe Übungen) Argumentieren/Kommunizieren -z.B. Vermutungen begründen, sachgerecht diskutieren, konstruktiv mit Fehlern umgehen (Teamarbeit, Fehlersuche), Arbeitsergebnisse vorstellen 2. Klassenarbeit Schriftliche Rechenverfahren -Schriftliches Addieren und Subtrahieren -Schriftliches Multiplizieren -Schriftliches Dividieren -vermischte und komplexe Übungen -offene Aufgaben Zahlen und Operationen -Rechnen flüssig im Kopf, halbschriftlich und schriftlich und nutzen dabei Rechenvorteile -nutzen die multiplikative Struktur natürlicher Zahlen (Teiler, Vielfache, Primzahlen, Teilbarkeitsregeln) Buch S. 106 - 127 Offene Aufgaben Arbeitsblätter Fermi - Aufgaben Symbolische, formale und technische Elemente -Zahlenterme berechnen, zwischen Umgangssprache und Symbolsprache übersetzen, Sachsituationen durch Gleichungen darstellen Geometrische Körper und Figuren -Körper - Ecken, Kanten, Flächen -Vielecke - Koordinatensystem -Geraden und Beziehungen zwischen Geraden -Rechtecke - Parallelogramme Trapeze - Drachen -Netze und Schrägbilder von Quader und Würfel -Kreise - Komplexe Übungen -offene Aufgaben 4. Klassenarbeit Buch S. 134 - 177 Offene Aufgaben Arbeitsblätter Fermi - Aufgaben Raum und Form -erkennen und benennen Eigenschaften einfacher ebener Figuren und zeichnen diese -erkennen und benennen Eigenschaften einfacher ebener Körper und fertigen Modelle, Skizzen, Schrägbilder an -erstellen und erkennen Würfel- und Quadernetze -Gerade, Strahl, Strecke -senkrecht, parallel Größen und Messen -entnehmen Originallängen aus Zeichnungen und maßstäblichen Karten Funktionaler Zusammenhang -stellen Beziehungen zwischen Zahlen und Größen in Diagrammen(Koordinatensystem)dar Modellieren/Problemlösen -z.B. Fragen formulieren, mathematische Modelle wählen, selbst Fragen stellen, auf „Entdeckungsreise“ gehen, das Problem mit eigenen Worten formulieren, Probleme durch Probieren lösen, Sachaufgaben, vermischte und komplexe Aufgaben Argumentieren /Kommunizieren -z.B. Vermutungen begründen, sachgerecht diskutieren, Lösungen vorstellen und erklären, Fehler suchen und korrigieren Symbolische, formale und technische Elemente -mit Lineal, Geodreieck und Zirkel arbeiten Anteile - Brüche -Teile eines Ganzen - Brüche -Brüche als Maßzahlen in Größenangaben Brüche als Teiler mehrerer Ganzer -Bestimmen eines Teils von einer Größe -Vergleichen und Ordnen von Brüchen -Bestimmen von Anteilen bei beliebigen Größen -Angaben von Anteilen in Prozent -Addieren und Subtrahieren von gleichnamigen Brüchen -Vervielfachen von Brüchen -Dezimalbrüche -offene Aufgaben Buch S. 180 - 218 Offene Aufgaben Arbeitsblätter Material zum Legen Fermi - Aufgaben Modellieren/Problemlösen -z.B. Fragen formulieren, Modelle wählen, auf „Entdeckungsreise“ gehen, Sachaufgaben, vermischte und komplexe Übungen Argumentieren/Kommunizieren -z.B. Vermutungen begründen, sachgerecht diskutieren, mit Fehlern konstruktiv umgehen (Teamarbeit, Fehlersuche) 5. Klassenarbeit Flächeninhalt -Flächenvergleich - Messen von Flächen -Umwandeln in andere Flächeneinheiten, Kommaschreibweise -Rechnen mit Flächeninhalten -Berechnungen am Rechteck -vermischte und komplexe Zahlen und Operationen -Notwendigkeit der Zahlbereichserweiterung auf die Bruchzahlen anhand von Beispielen erläutern -handelnd Bruchzahlen erzeugen -vielfältige Vorstellungen von Bruchzahlen haben -Brüche ordnen und vergleichen -verschiedene Darstellungen von Bruchzahlen verwenden -Addition und Subtraktion mit überschaubaren Nennern -multiplizieren einfacher Brüche mit natürlichen Zahlen -identifizieren Brüche mit dem Nenner 100 als Prozent Buch S. 222 - 245 Arbeitsblätter Offene Aufgaben Fermi - Aufgaben Größen und Messen -Flächeninhalt und Längen unterscheiden -Einheiten situationsgerecht wählen und umrechnen, den Umrechnungsfaktor erläutern -Flächeninhalt von Quadrat und Rechteck rechnerisch und durch Messung bestimmen, -Flächenmessungen durchführen Modellieren/Problemlösen Übungen -offene Aufgaben -„Stelle selbst Fragen“,“Gehe auf Entdeckungsreise“, Sachaufgaben, vermischte und komplexe Übungen Argumentieren/Kommunizieren -z.B. Vermutungen anstellen und begründen, sachgerecht diskutieren, mit Fehlern konstruktiv umgehen, Teamarbeit 6. Klassenarbeit Symbolische,formale und technische Elemente -Umgang mit Lineal und Geodreieck Daten erheben, auswerten und darstellen -Statistische Erhebungen -Mittelwert -vermischte und komplexe Übungen -offene Aufgaben Buch S. 246 - 259 Eigene Erhebungen Offene Aufgaben Daten und Zufall -Daten sammeln, Datentypen unterscheiden, Daten in Säulen- und Balkendiagrammen darstellen (absolute Häufigkeit) -Datenverteilungen beschreiben, Daten interpretieren Modellieren/Problemlösen -siehe oben Argumentieren/Kommunizieren -siehe oben Darstellen -aus Darstellungen Informationen beschaffen -einfache Darstellungen erstellen Schuleigener Lehrplan für das Fach Mathematik Jahrgang 6 Lehrbuch: Mathematik heute 6 Inhalte Materialien Kompetenzen gemäß Kerncurriculum Volumen (Rauminhalt) - Volumenvergleich - Messen von Flächen -Umwandeln in andere Volumeneinheiten Kommaschreibweise -Rechnen mit Volumina -Berechnungen am Quader -vermischte und komplexe Übungen -offene Aufgaben Buch S. 6 - 31 Größen und Messen -Längen, Flächen und Volumina unterscheiden -schätzen Größen durch Vergleich mit alltagsbezogenen Repräsentanten -wählen Einheiten situationsgerecht aus und rechnen benachbarte Einheiten ineinander um -ermitteln durch Messung das Volumen von Würfel und Quader - Messungen in der Umwelt durchführen -Volumen von Würfel und Quader berechnen Arbeitsblätter Modelle Offene Aufgaben Fermiaufgaben Modellieren/Problemlösen -z.B. Fragen selbst formulieren, mathematische Modelle wählen, auf „Entdeckungsreise“ gehen, Sachaufgaben, vermischte und komplexe Übungen eventuell hier 1.Klassenarbeit oder aber nach dem nächsten Thema Winkel Argumentieren/Kommunizieren -z.B. Vermutungen anstellen und begründen, sachgerecht diskutieren, in Team arbeiten, Fehler suchen Symbolische, formale und technische Elemente -mit Lineal und Geodreieck sachgerecht arbeiten Winkel -Winkel messen und zeichnen -Winkel an Geradenkreuzungen Sätze über Winkelbeziehungen -vermischte und komplexe Übungen Buch S. 32 - 54 Arbeitsblätter Offene Aufgaben Fermi - Aufgaben Größen und Messen - Winkelmessungen durchführen -Winkeltypen unterscheiden (Scheitel-,Stufen-,Neben,Wechselwinkel -Winkelbeziehungen an Parallelen nutzen Eigene Bemerkungen -offene Aufgaben Modellieren/Problemlösen -z.B. Fragen formulieren, Modelle wählen, auf „Entdeckungsreise“ gehen, Probleme mit eigenen Worten formulieren, Probleme anders darstellen oder durch Probieren lösen, Informationen aus Texten entnehmen, Sachaufgaben lösen eventuell hier 1.Klassenarbeit Argumentieren/Kommunizieren -z.B. Vermutungen begründen, sachgerecht diskutieren (eingeführte Fachbegriffe und Darstellungen benutzen), mit Fehlern konstruktiv umgehen, im Team arbeiten und die Ergebnisse darstellen Symbolische, formale und technische Elemente -mit Lineal und Geodreieck sachgerecht arbeiten Bruchzahlen -Bruch als Quotient natürlicher Zahlen -Erweitern und Kürzen -Anteile von beliebigen Größen drei Grundaufgaben -Verhältnisse und Anteile -Zahlenstrahl - Bruchzahlen -Vergleichen und Ordnen von Bruchzahlen -vermischte und komplexe Übungen -offene Aufgaben 2.Klassenarbeit Buch S. 56 - 84 Arbeitsblätter Handlungsorientiertes Material Offene Aufgaben, z.B. Fermi - Aufgaben Zahlen und Operationen -erläutern die Notwendigkeit der Zahlbereichserweiterung auf die Bruchzahlen anhand von Beispielen -Handlungen benennen, die Bruchzahlen erzeugen -vergleichen und ordnen positive rationale Zahlen -die vier Grundrechenarten auf Brüche mit überschaubaren Nennern anwenden Modellieren/Problemlösen -z.B. Fragen formulieren, geeignete Modelle wählen, Auf „Entdeckungsreise“ gehen, Sachaufgaben lösen, vermischte und komplexe Übungen durchführen Argumentieren/Kommunizieren -z.B. Vermutungen aufstellen und begründen, Rechnen mit Bruchzahlen -Addieren und Subtrahieren von Bruchzahlen -Vervielfachen und Teilen von Brüchen -Multiplizieren von Bruchzahlen -Dividieren von Bruchzahlen -Vorteilhaft rechnen mit Bruchzahlen - Rechengesetze -vermischte Übungen zu allen Rechenarten -komplexe Übungen -offene Aufgaben Buch S.86 - 126 sachgerecht diskutieren, konstruktiv mit Fehlern umgehen und im Team arbeiten und die Ergebnisse darstellen Arbeitsblätter Offene Aufgaben Fermi - Aufgaben 3.Klassenarbeit Symmetrie -Achsensymmetrie - Spiegeln an einer Geraden -Verschieben einer Figur -Punktsymmetrie -Symmetrische Dreiecke und Vierecke -vermischte und komplexe Übungen -offene Aufgaben 4. Klassenarbeit Buch S. 128 - 158 Arbeitsblätter Offene Aufgaben Fermi - Aufgaben Spiegel Handlungsorientierte Aufgaben Raum und Form -Symmetrien erkennen und benennen, achsensymmetrische Figuren konstruieren und Muster (Bandornamente) fortsetzen Modellieren /Problemlösen -z.B. Fragen formulieren, mathematische Modelle wählen („Stelle selbst Fragen“,“Gehe auf Entdeckungsreise“, Sachaufgaben verstehen, erklären, lösen Argumentieren/Kommunizieren -z.B. mit Fehlern konstruktiv umgehen( Teamarbeit, Fehlersuche), Arbeitsergebnisse präsentieren, Vermutungen aufstellen und begründen, sachgerecht diskutieren Symbolische, formale und technische Elemente -sachgerecht mit Lineal und Geodreieck umgehen Dezimalbrüche -Dezimalbrüche und gewöhnliche Brüche -Vergleichen von Dezimalbrüchen Runden -Addieren und Subtrahieren von Dezimalbrüchen -Multiplizieren und Dividieren von Dezimalbrüchen vermischte Übungen zu allen Rechenarten Buch S. 160 - 212 Arbeitsblätter Offene Aufgaben Fermi - Aufgaben Zahlen und Operationen -Zahlen auf der Zahlengeraden und in der Stellenwerttafel darstellen, -Dezimalbrüche vergleichen und ordnen -sachangemessen runden -geben Grenzen an, zwischen denen eine gerundete Zahl liegt -rechnen im Kopf, hanbschriftlich und schriftlich, wählen das Verfahren sinnvoll aus, nutzen Rechenvorteile -rechnen mit Dezimalbrüchen in Sachsituationennutzen verschiedene Kontrollverfahren eventuell hier 5. Klassenarbeit -Berechnen von Flächen und Körpern -periodische Dezimalbrüche -Terme mit gewöhnlichen und Dezimalbrüchen -Gleichungen mit Dezimalbrüchen -komplexe Übungen -offene Aufgaben Modellieren/Problemlösen -z.B. Fragen formulieren, mathematische Modelle wählen, selbst Fragen stellen, auf Enrdeckungsreise gehen, Sachaufgaben lösen, vermischte und komplexe Übungen bearbeiten Argumentieren/Kommunizieren - z.B. Vermutungen aufstellen und begründen, sachgerecht diskutieren, im Team arbeiten, konstruktiv mit Fehlern umgehen, Arbeitsergebnisse vorstellen und erklären 5. Klassenarbeit eventuell auch schon vorher Zuordnungen -Zuordnungstabellen -Graph einer Zuordnung -Proportionale Zuordnungen -vermischte und komplexe Übungen Buch S. 214 - 238 Arbeitsblätter Offene Aufgaben Fermi - Aufgaben Funktionaler Zusammenhang -Zusammenhänge zwischen zwei Größen als proportional erfassen -Größen rechnerisch und graphisch in proportionalen Zusammenhängen bestimmen (Dreisatz) Zahlen und Operationen -lösen Sachprobleme mit proportionaler Struktur 6. Klassenarbeit Modellieren/Problemlösen -z.B.: Fragen formulieren, mathematische Modelle wählen, auf “Entdeckungsreise“ gehen, Sachaufgaben, vermischte und komplexe Aufgaben Argumentieren/Kommunizieren -z.B.: Vermutungen begründen, sachgerecht diskutieren, konstruktiv mit Fehlern umgehen (Teamarbeit, Fehlersuche) Zufall und Wahrscheinlichkeit -Zufallsexperimente und Wahrscheinlichkeit -Wahrscheinlichkeit und relative Häufigkeit Buch S.240 - 254 Handlungsorientierte Aufgaben Daten und Zufall -Laplace - Experimente durchführen, deren Wahrscheinlichkeit qualitativ(„wahrscheinlich“, „sicher“, “genauso wahrscheinlich wie“, “unmöglich“) und durch Brüche beschreiben Zahlen und Operationen -bestimmen die Anzahl der Möglichkeiten durch systematische Überlegung (Kombinatorik) Modellieren/Problemlösen -z.B.: Fragen formulieren, mathematische Modelle wählen, Sachaufgaben Argumentieren/Kommunizieren -begründen Vermutungen, diskutieren sachgerecht Zusatzinformationen: Offene Aufgaben ( z.B. Aufgaben, die mehrere Lösungsansätze bieten und bei denen nur wenige Angaben gegeben sind, sodass die Informationen selbst recherchiert und besorgt werden müssen) sollen von den Fachkollegen gesammelt und zu einem Fundus zusammengestellt werden, am besten jahrgangsweise. Es wird empfohlen, so oft wie möglich solche Aufgaben im Unterricht einzusetzen, weil dadurch einerseits besonders die prozessorientierten Kompetenzen geschult, aber auch inhaltsbezogene Kompetenzen wiederholt und präsent gehalten werden. Aufgabensammlungen mit offenen Aufgaben: - Fermi - Aufgaben (Kästchen mit offenen Aufgaben von Herrn Fermi) - Palma Mathematik heute, Kompetenzorientierte Aufgaben mit Kommentaren, Band 1 und 2 -