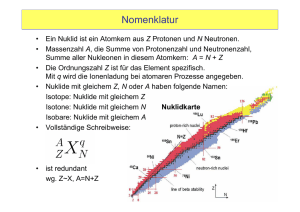
1 Atomphysik Kernphysik 27 10 08

Atomphysik & Kernphysik
Prof Dr.
Prof.
Dr Sabine Mahling
Naturwissenschaftliche Grundlagen EEB, CEB und SSB
@designed by ms
Inhalte
1. Grundbegriffe
1
2. Materiebegriff
3. Atommodelle
1. DALTONsche
Atomhypothese
2. THOMSONsches
Atommodell
3. RUTHERFORDsches
Atommodell
4. BOHRsches
Atommodell
5. Wellenmechanisches
Atommodell
6. Das Standardmodell
4.
4
5.
6.
7.
8.
Periodensystem
Nuklidkarte
Antimaterie
Radioaktivität
Kernphysik
1. Nukleonenmassen
2. Massendefekt
3. Die 4 fundamentalen
Kräfte
4. Kernspaltung
5. Kernreaktionen
1
1 Einige Grundbegriffe
...
Masse m
Atommasse M
Molzahl n
Druck p
Temperatur T
Energie E
Wärme Q
Arbeit W
Entropie S
Wirkungsgrad η
...
1.1 Physikalische Einheiten
Volumen
Druck
Energie
Temperatur
Zeit
Stoffmengen
V
p
E
T
t
n
m3
N/m2 = Pa
J = Nm
K
s
mol
2
1.1.1 Das SI-System
SI = Système
y
International d' Unités
IS = International System of Units
Basisgröße
Basiseinheit Abkürzung
Länge
Masse
Stromstärke
Zeit
Temperatur
Lichtstärke
Stoffmenge
Ebener Winkel
Raumwinkel
Meter
Kilogramm
Ampere
Sekunde
Kelvin
Candela
Mol
Radiant
Steradiant
m
kg
A
s
K
cd
mol
rad
sr
http://www.chemie.fu-berlin.de/chemistry/general/si.html
1.1.1.1 Der Raumwinkel
A
• Der Raumwinkel Ω einer beliebigen Fläche A entspricht dem
Quotienten aus der Fläche S (die sich ergibt, wenn A auf eine
Kugel vom Radius r projiziert wird) und dem Kugelradius r2:
Ω=
S
r2
http://de.wikipedia.org
3
1.1.1.2 Die Einheit des
Raumwinkels
Raumwinkel: Verhältnis zweier Flächen Æ SI Æ 1 m²/m²;
SI-Name:
Steradiant
Einheit-Zeichen
sr
1 sr = 1 m²/m² = 1
das Einheit-Zeichen sr kann auch weggelassen werden (nicht
jedoch bei Anwendungsfeldern, bei denen intensiv mit
Raumwinkeln gerechnet wird, z.B. in der Lichttechnik).
Die SI-Einheiten für Lichtstärke und Lichtstrom unterscheiden sich
nur durch Steradiant.
Übungsaufgabe
?
Wi groß
Wie
ß ist
i t der
d Raumwinkel
R
i k ld
der vollen
ll
Kugeloberfläche ?
4
1.1.1.3 Polarkoordinaten der
Ebene
Die Polarkoordinaten ((Kreiskoordinaten)) eines Punktes in der
euklidischen Ebene werden in Bezug zu einem Koordinatenursprung
(einem Punkt der Ebene) und einer Polarkoordinatenrichtung (ein im
Koordinatenursprung beginnender Strahl) angegeben
http://de.wikipedia.org
1.1.1.4
Polarkoordinatenumrechnung
Polar zu kartesisch lässt sich folgendermaßen umrechnen:
x = r cos ( φ )
y = r sin ( φ )
Für kartesisch zu polar gelten die folgenden Formeln:
r = x2 + y 2
⎛ x⎞
für y ≥ 0
⎝r⎠
⎛ x⎞
ϕ = − arccos⎜ ⎟ für y < 0
⎝r⎠
ϕ = arccos⎜ ⎟
5
1.1.1.5 Raumwinkel und
Polarkoordinaten
Ein Punkt in der Ebene lässt sich in Polarkoordinaten durch (Flächen-) Winkel
und Radius angeben. Auch im Raum gibt es ein solches Koordinatensystem.
Der Raumwinkel ist dafür jedoch nicht ausreichend. Neben dem Radius sind
immer die zwei Flächenwinkel Meridianwinkel φ und Breitenwinkel γ nötig.
Allerdings besteht ein Zusammenhang zwischen dem Raumwinkel Ω und den
beiden Winkeln der Raumpolarkoordinaten:
Ω=
ϕ2 γ 2
∫ ∫ sin γ ⋅ dγ ⋅ dϕ
ϕ1 γ 1
http://de.wikipedia.org
1.1.1.6 Polarkoordinaten des
Raumes
In räumlichen Polarkoordinaten wird ein Punkt durch seinen Abstand vom
Ursprung r , sowie durch zwei Winkel θ und ϕ angegeben. Wenn der Abstand
vom Ursprung konstant ist (auf einer Sphäre), benötigt man nur die zwei
Winkel, um einen Punkt eindeutig zu bezeichnen, und spricht dann von
sphärischen Koordinaten. Der Begriff Kugelkoordinaten kann als
Oberbegriff für diese beiden Fälle angesehen werden.
http://de.wikipedia.org
6
1.1.2 Vorsilben
Vorsilbe Abkürzung Zehnerpotenz Dezimalzahl
FemtoPicoNanoMikroMilliKil
Kilo
Mega
Giga
Tera
Peta
f
p
n
µ
m
k
M
G
T
P
10 E-15
10 E-12
10 E-09
10 E-06
10 E-03
10 E+03
E 03
10 E+06
10 E+09
10 E+12
10 E+15
0.000 000 000 000 001
0.000 000 000 001
0.000 000 001
0.000 001
0.001
1000
1000000
1000000000
1000000000000
1000000000000000
http://physics.nist.gov/cuu/Units/prefixes.html
1.1.3 Griechische Buchstaben
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
α
β
γ
δ
ε
ζ
η
θ ϑ
θ,
ι
κ
λ
μ
=
=
=
=
=
=
=
=
=
=
=
=
Alpha
Beta
Gamma
Delta
Epsilon
Zeta
Eta
Th t
Theta
Jota
Kappa
Lambda
My
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
υ
ξ
ο
π
ρ
σ
τ
υ
φ, ϕ
χ
ψ
ω
=
=
=
=
=
=
=
=
=
=
=
=
Ny
Xi
Omikron
Pi
Rho
Sigma
Tau
Y il
Ypsilon
Phi
Chi
Psi
Omega
7
1.1.4 Avogadrozahl und Mol
Avogadrozahl:
g
Anzahl der Atome in 12 g des Kohlenstoff-Isotops
p C-12,,
gleichzeitig: Anzahl von Atomen oder Molekülen in der Stoffmenge von
einem Mol und hat nach der CODATA-Empfehlung aus dem Jahr 2002
den Zahlenwert
Ein Mol eines Stoffes enthält stets
NA = NL = 6,0221415(10) 1023 mol − 1
Molekulargewicht, angegeben in Gramm = 1 Mol
1 Mol He = 4,003 g
1 Mol N2 = 14,007 x 2
= 28,014 g
1 Mol NaCl = 22,990 + 35,453 = 58,443 g
http://physics.nist.gov/cuu/Constants/index.html
http://de.wikipedia.org/
1.1.5 Atomic Unit u
12 g C ≡ 6,0221415(10) 1023 C-Atome
12
6,022 ⋅ 1023
= 12u
[ g]
1
6,022 ⋅ 1023
[ g]
1 C
≅
1 u
=
http://physics.nist.gov/cuu/Constants/index.html
8
1.1.6 Druck
p=
F
A
Druck = Kraft / Fläche
Pascal: Pa = N/m2 = kg/m s2
1b = 100 000 P
1bar
Pa ~ atmosphärischer
t
hä i h L
Luftdruck
ftd k
Normaldruck
Standarddruck
p = 1 atm = 101,325 kPa = 1013,25 mbar
p = 1 atm = 101,325 kPa = 1013,25 mbar
http://www.ebgymhollabrunn.ac.at/ipin/ph-druck.htm
http://cicum92.cup.uni-muenchen.de/puchinger/glossar/glossarB2.html
1.1.7 Abgeleitete Größen
Geschwindigkeit
g
v
v=
l
t
l
t
D=
= Weg
= Zeit
⎡m⎤
⎢⎣ s ⎥⎦
Strahlungsdosis
g
D
[m]
[s]
E
m
E = Energie
m = Masse
[J]
[kg]
⎡
J ⎤
⎢ Sv = kg ⎥
⎦
⎣
http://www.chemie.fu-berlin.de/chemistry/general/si.html
9
2 Was ist Materie ?
Was ist Materie ?
Was ist ein Stoff ?
Materieaggregationen
2.1 Masse-Energie
Das Weltall besteht aus Materie und strahlender Energie.
Materie ist jegliche Art von Masse -Energie,
die sich langsamer als Licht fortbewegt,
strahlende Energie dagegen, ist jegliche Art von Masse-Energie,
die sich mit Lichtgeschwindigkeit bewegt
Linus Pauling
E = m.c2
10
2.2 Das Universum
Universum:
Gesamtheit aller Objekte im Kosmos,
Weltall
Beschreibung durch die allgemeine
Relaltivitätstheorie
Entstehung durch „Urknall“
Alter: 13,7 Milliarden Jahre
Kosmos:
Weltraum, Weltordnung
Weltraum:
Beginnt in 80 - 100 km Höhe
http://de.wikipedia.org/
2.2.1 Der Urknall
Urknall = Beginn des Universums nach kosmologischem Modell
gemeinsame Entstehung von Materie, Raum und Zeit aus einem Ursprung
ständige Expansion nach den Gesetzen der allgemeinen Relativitätstheorie
„Beweise“ für die Urknalltheorie:
• Die Rotverschiebung der Galaxien und damit die derzeitige Expansion des
Universums
• Das
D S
Spektrum
kt
d
der Hi
Hintergrundstrahlung
t
d t hl
d
des U
Universums
i
• Die Grenze in der Altersverteilung der Sterne bei etwa 13 Milliarden Jahren
• Die Häufigkeit der Elemente im Weltraum (insbesondere Wasserstoff,
Deuterium und die Isotope des Helium)
11
2.2.2 Frühgeschichte des
Universums
1 Billion = 1 Milliarde !
http://www.raumfahrer.net/astronomie/kosmologie/urknall.shtml
2.3 Der Aufbau der Erde
Anteile der Elemente an der Erdkruste in g / t
Metalloxide, Silikate
T = 2000 °C
Fe, Ni
Fe
Ni, S (flüssig)
T = 2900 °C
Æ Erdmagnetfeld
Fe, Ni, (fest)
p = 4 . 106 bar
T = 4000 –5000 °C
O
Si
Al
Fe
Ca
Na
K
Mg
Ti
H
P
Mn
F
S
466.000
277.200
81.300
50.000
36.300
28.300
25 900
25.900
20.900
4.400
1.400
1.180
1.000
700
520
http://de.wikipedia.org/wiki/Innerer_Aufbau_der_Erde
12
2.4 Elemente und Verbindungen
Chemisches Element
Unter einem chemischen Element versteht man einen Stoff,
der sich chemisch nicht mehr weiter in andere Stoffe
zerlegen lässt.
Chemische
Ch
i h Verbindung
V bi d
Unter einer chemischen Verbindung versteht man einen
Stoff, der aus Atomen mehrerer verschiedener Elemente
besteht und einheitliche physikalisch-chemische
Eigenschaften wie z.B. Schmelz- und Siedepunkt aufweist.
2.4.1 Der Atombegriff
• Atome sind die -einst als unteilbar geglaubten- kleinsten
Bestandteile der der chemischen Elemente, die dessen
Ei
Eigenschaften
h ft aufweisen
f i
• Unter einem chemischen Element versteht man einen Stoff, der
aus Atomen mit gleichen chemischen Eigenschaften aufgebaut
ist.
13
3 Atommodelle
Vordenker:
• Demokrit (ca. 500 v.Chr.): Alle Stoffe bestehen aus definierten
kleinsten Teilchen den Atomen von Atomos Teilchen des Unteilbaren
• Daniel Sennert (1618): Gesetz der Erhaltung der Elemente. Bei einer
chemischen Reaktion gehen Elemente weder verloren, noch werden
Elemente neu geschaffen.
• Robert Boyle (1661): Elemente sind bestimmte primitive und einfache,
völlig unvermischte Körper, sie enthalten keine anderen Körper, sie
sind Zutaten, aus denen alle perfekt gemischten Körper
zusammengesetzt sind und in welche diese letztlich zerlegt werden.
• Antoine Laurent de Lavoisier (1785): Gesetz der Erhaltung der Masse.
Die Summe der Massen der Edukte ist stets gleich der Summe der
Massen der Produkte.
• Jeremias Benjamin Richter (1791/92): Gesetz der äquivalenten
Proportionen.
http://de.wikipedia.org
3.1 Die DALTONsche
Atomhypothese
Daltons Atomhypothese (1808)
•
•
•
•
•
Materie besteht aus kleinsten kugelförmigen Teilchen oder Atomen.
Diese Atome sind unteilbar und können weder geschaffen noch zerstört
werden.
Alle Atome eines chemischen Elements sind untereinander gleich, sie
unterscheiden sich jedoch nur in der Masse von denen anderer.
Diese Atome können chemische Bindungen eingehen und aus diesen
auch wieder gelöst werden.
Das Teilchen einer Verbindung wird aus einer bestimmten, stets
gleichen Anzahl von Atomen der Elemente gebildet, aus denen die
Verbindung besteht
http://de.wikipedia.org
14
3.2 Das THOMSONsche
Atommodell
Rosinenkuchenmodell
Atom hat gleich viele positive und negative Bestandteile
Atom ist in der Summe elektrisch neutral
Negative Ladung
Positive Ladung
3.3 Das RUTHERFORDsche
Atommodell
At k
Atomkernmodell:
d ll winziger
i i
K
Kern = M
Massepunkt
kt
Planetenmodell: Elektronen bewegen sich auf Kreisbahnen um den Kern
Kreisbahn entsteht durch Gleichgewicht von Coulomb- und Zentrifugalkraft
Negative Ladung
Positive Ladung
Widerspruch zu den Gesetzen der Elektrodynamik ! Æ instabile Elektronenbahnen
15
3.3.1 Das RUTHERFORD-Experiment
α
Goldfolie
Film
Streuung von Alphateilchen an Goldfolie erklärbar
Berechnung einfacher Atomspektren möglich
3.4 Das BOHRsche Atommodell
φ = 10-7 - 10-10 m
Kern:
Protonen
Neutronen
(+)
(n)
Elektronenhülle:
Elektronen
(-)
Widerspruch zu den Gesetzen der Elektrodynamik ! Æ Bremsstrahlung erwartet !
16
3.4.1 Stabile Elektronenbahnen
1. BOHRsche Quantenbedingung:
stabile Bahnen wenn das Produkt aus Kreisumfang und Elektronenimpuls ein
Vielfaches des PLANCKschen Wirkungsquantums h ist
(2 ⋅ π ⋅ rn ) ⋅ (me ⋅ vn ) = n ⋅ h
n = Schalennummer, rn = Radius Schale n, me = Elektronenmasse, vn = Impuls
Schale n
2. BOHRsche Frequenzbedingung:
g g
Durch Energiezufuhr ist ein Übergang zwischen den Bahnen möglich, wenn
absorbierte Energie genau der Energiedifferenz ΔE zwischen den Bahnen
entspricht:
ΔE = h ⋅ν = E2 − E1
E1 = Energie Schale 1, E2 = Energie Schale 2, ν = Frequenz
3.4.2 Elektronen Schalen
2n2 Elektronen pro Schale
E
n = 4 N-Schale
n = 3 M-Schale
n = 2 L-Schale
n = 1 K-Schale
1 Z ⋅ e 2 me ⋅ Z 2 ⋅ e 4
En = − ⋅
=
2 rn
2 ⋅ n2 ⋅ h2
En
n
Z
e
rn
me
=
=
=
=
=
=
h =
Schalenenergie
Schalennummer
Ordnungszahl
Elementarladung
Orbitalradius
Elektronenmasse
h / 2π
17
3.4.3 Die Wasserstoffspektrallinien
Spektrum
p
des Wasserstoffatoms
P
O
N
M
L
PFUND
BRACKETT
PASCHEN
BALMER
K
LYMAN
Spektralserien
3.4.4 Das Wasserstoffspektrum
http://www.physics.utoledo.edu/
18
3.4.5 Relativer Atomdurchmesser
Haselnuss
100 m
1 cm
3.5 Wellenmechanisches
Atommodell
Elektron = stehende Welle
Wellenfunktion eines Elektrons
Ψ (r,E)
Aufenthaltsbereich eines Elektrons
Ψ 2(r,E)
SCHRÖDINGER Gleichung
SCHRÖDINGER-Gleichung
HΨ = EΨ
Energiezustände eines Elektrons
E
Kernabstand
r
19
3.5.1 Stehende Welle
l = n⋅
λ
2
n = 1,2,3,4,...
http://uni-ka.lanable.de/html/exphys1/exse18.htm
3.5.2 Wellenmechanikprinzipien
Quantenmechanik
• Welle – Teilchen Dualismus
λ=
h
p
• Wellenmechanik: Teilchen Æ Wellenfunktion Ψ
1.
1
2.
3.
4.
komplexwertig
keine Messgröße
Ψ2 (Betragsquadrat) Aufenthaltswahrscheinlichkeit des Teilchens
Ψ (r,θ,ϕ,t) Æ SCHRÖDINGER-Gleichung
20
3.5.2.1 Klassische Teilchen
klassische Teilchen sind Bausteine der Materie, wie in der klassischen
Physik verstanden, wird mit folgenden Eigenschaften:
• Ort:
• Impuls:
• Masse:
x
p = m⋅v =
m
E h ⋅ν
=
c
c
• keine Unschärferelation (Ort und Impuls können beliebig genau
bestimmt werden)
3.5.2.2 DE BROGLIE-Wellenlänge
• DE BROGLIE: auch massereiche Teilchen haben Wellencharakter
– 1923 "Dualität von Welle und Korpuskel"
– 1927 Bestätigung durch Doppelspaltexperiment von Clinton
Davisson und Lester Germer
• Hat das Teilchen einen Impuls p, so ist seine Wellenlänge λ :
λ=
h
p
p=
h ⋅ν
c
λ=
c
ν
c = Lichtgeschwindigkeit (299792458 ms-1)
h = PLANCKsches Wirkungsquantum
ν = Frequenz der Lichtwelle
21
3.5.2.3 Welle-Teilchen-Dualismus
• Wellen haben auch Teilchencharakter
• Teilchen haben auch Wellencharakter.
• Es sind stets beide Eigenschaften vorhanden
• Art der Beobachtung bedingt die Art der Erscheinung:
mikroskopische
ik k i h W
Wellenperspektive
ll
kti oder
d makroskopische
k k i h
(und somit unscharfen) Teilchenperspektive
3.5.2.4 Natur von Wellen und
Teilchen
Wellennatur
Teilchennatur
•
•
•
•
•
•
•
•
•
•
•
•
•
Wellenlänge, Amplitude
Wellenfunktion Ψ
O bit l Ψ2
Orbitale
Interferenzen
Stehende Wellen
Ausbreitungsgeschwindigkeit
Energie: E = h.ν
Masse, Impuls
Flugbahnen
I i ti
Ionisationsvermögen
ö
Geometrische Optik (Newton)
Geschwindigkeit
Energie: E = ½ m.v2
22
3.5.2.5 Interferenzen
http://de.wikipedia.org/
3.5.2.6 Makroskopische Gegenstände
Wellencharakter der Teilchen zeigt sich nicht bei makroskopischen
Gegenständen (Körpern), was zwei prinzipielle Ursachen hat:
– bei langsamer Bewegung haben Körper aufgrund großer Masse
eine Wellenlänge, die erheblich kleiner ist als ihre Abmessungen
Æ separate Beschreibung der Bestandteile.
– IIn makroskopischen
k k i h G
Gegenständen
tä d llaufen
f permanentt
thermodynamisch irreversible Prozesse ab Æ
Photonenaustausch, Wärmestrahlung Æ Dekohärenz des
Systems Æ nicht interferenzfähige Zustände Æ klassisches
Teilchen
http://de.wikipedia.org
23
3.5.3 Die Unschärferelation
• Für ein q
quantenmechanisches Teilchen ist es unmöglich
g
Ort x
und Impuls p gleichzeitig beliebig genau zu messen
Δx ⋅ Δp =
h
2
• Der Zeitpunkt t eines Vorganges und die dabei übertragene
Energie E lassen sich nicht gleichzeitig messen
Δt ⋅ ΔE =
h
2
• Je genauer eine dieser Größen bestimmt wird, desto ungenauer
erscheint die andere !
Quantenmechanische Aussagen sind Wahrscheinlichkeitsaussagen !
3.5.3.1 PLANCKsches
Wirkungsquantum
• Definition der Energie E:
E = h⋅
c
λ
h = 6,626 068 76 ⋅10 −34 Js
c = Lichtgeschwindigkeit, λ = Wellenlänge
• h hat die Dimension einer Wirkung !
24
3.5.4 Die Wellenfunktion des
Elektrons
All
Allgemeine
i W
Wellenfunktion
ll f kti fü
für monochromatische
h
ti h W
Welle
ll iin r-Richtung
Ri ht
Ψ (r , t ) = c ⋅ ei (ϖt + kr )
Realer Anteil der Wellenfunktion
Ψ (r , t ) = c ⋅ cos(ϖ ⋅ t + k ⋅ r )
Zustandsfunktion
3.5.5 Stehende Wellen
Stehende Wellen
• sind Wellen, bei denen die räumliche Lage der Schwingungsbzw. Wellenbäuche und –knoten sich zeitlich nicht ändert;
• sind Wellen, die keine Energie transportieren
Für die Strecke l, auf der die Schwingung stattfindet, muss gelten,
dass sie ein Vielfaches n der Wellenlänge λ ist.
l = n⋅
λ
2
n = 1,2,3,4,...
d
l
25
3.5.5.1 Stehende Wellen (a)
l = n⋅
λ
2
n = 1,2,3,4,...
d
l
d
n = 1 Grundschwingung
n = 2 1. Oberschwingung
d
d
n = 3 2. Oberschwingung
n = 4 3. Oberschwingung
3.5.5.2 Stehende Wellen (b)
d
d
n = 1 Grundschwingung
d
n = 2 1. Oberschwingung
d
n = 3 2. Oberschwingung
n = 4 3. Oberschwingung
Balkendiagrammdarstellung
26
3.5.5.3 Stehende Wellen (c)
325,00
40,00
320,00
45,00
315
315,00
00
50
50,00
00
310
310,00
00
55
55,00
00
305,00
60,00
300,00
65,00
295,00
70,00
290,00
75,00
285,00
80,00
280,00
85,00
275,00
90,00
270,00
95,00
265,00
100,00
260,00
105,00
255,00
110,00
250,00
115,00
245,00
120,00
240,00
125,00
235,00
130,00
230,00
135,00
225,00
140,00
220,00
145,00
215,00
150,00
210,00
155,00
205,00
160,00
200,00
165,00
195,00
170,00
190,00
185,00 180,00
175,00
n = 1 Grundschwingung
,
,
335,00
30,00
330,00
35,00
325,00
40,00
320,00
45,00
315,00
50,00
310,00
55,00
305,00
60,00
300
300,00
00
65
65,00
00
295
295,00
00
70
70,00
00
290,00
75,00
80,00
285,00
280,00
85,00
275,00
90,00
270,00
95,00
265,00
100,00
260,00
105,00
255,00
110,00
250,00
115,00
245,00
120,00
240,00
125,00
235,00
130,00
230,00
135,00
225,00
140,00
220,00
145,00
215,00
150,00
210,00
155,00
205,00
160,00
200,00
165,00
195,00
170,00
190,00
185,00 180,00
175,00
n = 3 2. Oberschwingung
360,00 5,00
355,00
10,00
350,00
15,00
345,00
20,00
340,00
25,00
335
335,00
00
30,00
30
00
330
330,00
00
35
35,00
00
325,00
40,00
320,00
45,00
315,00
50,00
310,00
55,00
305,00
60,00
300,00
65,00
295,00
70,00
290,00
75,00
285,00
80,00
280,00
85,00
275,00
90,00
270,00
95,00
265,00
100,00
260,00
105,00
255,00
110,00
250,00
115,00
245,00
120,00
240,00
125,00
235,00
130,00
230,00
135,00
225,00
140,00
220,00
145,00
215,00
150,00
210,00
155,00
205,00
160,00
200,00
165,00
195,00
170,00
190,00
185,00 180,00
175,00
n = 2 1. Oberschwingung
360,00 5,00
355,00
10,00
350,00
15,00
345,00
20,00
340,00
25,00
335,00
30,00
330,00
35,00
325,00
40,00
320,00
,
, 00
45,00
315
315,00
00
50
50,00
310
310,00
00
55
55,00
00
305,00
60,00
300,00
65,00
295,00
70,00
290,00
75,00
285,00
80,00
280,00
85,00
275,00
90,00
270,00
95,00
265,00
100,00
260,00
105,00
255,00
110,00
250,00
115,00
245,00
120,00
240,00
125,00
235,00
130,00
230,00
135,00
225,00
140,00
220,00
145,00
215,00
150,00
210,00
155,00
205,00
160,00
200,00
165,00
195,00
170,00
190,00
185,00 180,00
175,00
n = 4 3. Oberschwingung
Polarkoordinatendarstellung
3.5.7 Der Drehimpuls des
Elektrons
• Ein Elektron mit der Masse m und
der Ladung e, das sich mit der
r
Geschwindigkeit v auf einem Kreis
r
mit dem Radius r bewegt hat ein
r
magnetisches Dipolmoment
μ und
r
einen Drehimpuls L von:
r r r
L=r×p
r
r
p = m⋅v
r
L
r
r
m -e
m,-e
Bahndrehimpuls
r
v
r
μ
Linearer Impuls
( 2 ⋅ π ⋅ r ) ⋅ ( m ⋅ v) = n ⋅ h
r r
L ,μ
gekoppelt
27
3.5.8 Der Spin des Elektrons
Elektronen weisen eine Drehung um die eigene Achse auf, damit
verbinden ist ein Eigendrehimpuls, den man auch als Spin
bezeichnet
r
S
Der Betrag des Spins kann die Werte annehmen:
S = s⋅h
Für das Elektron kann der Betrag des Spins nur sein:
s = ±1 2
3.5.9 Materiewellen
Materiewelle
L = l ⋅h
• Die Forderung im Bohrschen Atommodell, dass der Drehimpuls L
ein ganzzahliges Vielfaches von h = h / 2π ist, kann anschaulich
damit erklärt werden, dass eine Elektronenwelle um den Kern
"herumgewickelt"
herumgewickelt wird (l = Bahndrehimpulsquantenzahl).
Bahndrehimpulsquantenzahl) Wellen mit
einer Wellenlänge, die nicht Teiler des Umfangs ist, überlagern sich
bei mehrmaligem Wickeln destruktiv. Möglich - "erlaubt" - sind also
nur Wellen mit einer Wellenlänge, die den Umfang teilt. Dadurch
ergeben sich nach Bohr die diskreten Orbitale der Elektronen.
http://de.wikipedia.org
28
3.5.10 Quantenzahlen
Quantenzahlen sind einfache Zahlen, die den Zustand eines
quantenphysikalischen Systems beschreiben.
Durch einen vollständigen Satz von Quantenzahlen ist der Zustand
des Systems eindeutig festgelegt
3.5.10.1 Elektronenquantenzahlen
Quantenzahl
Hauptquantenzahl
Nebenquantenzahl
Magnetquantenzahl
Symbol
n
l
m
erlaubte Werte
1,2,3,4,5,...
0,1,2, ... (n-1)
0,±1,±2, ... ,± l
Bedeutung
Kernabstand, Energie
Bahndrehimpuls
Drehimpulsorientierung
Spinquantenzahl
s
±½
Eigendrehimpuls
der Bahndrehimpuls gibt den Orbitaltyp (s,p,d,f..) an;
die Drehimpulsorientierung gibt die Orbitallage .(bei p: x,y,z, etc) an
29
3.5.10.2 „Elektronenschalen“
• Alle Zustände mit demselben Wert für n bilden eine Schale,
– es gibt 2n2 Zustände in einer Hauptschale;
• Alle Zustände mit den selben Werten für n und l bilden eine
Unterschale,
– Alle Zustände in einer Unterschale haben dieselbe Energie
– Es gibt 2(2l+1) Zustände in einer Unterschale.
3.5.11 Atomorbitale
• Atomorbitale AO sind 3-dimensionale stehende Materiewellen,
die den Aufenthaltsbereich (keine klar definierte Bahn !) der
Elektronen darstellen. Das energieärmste Orbital entspricht dem
Grundzustand (Grundschwingung), energiereichere Orbitale
entsprechen angeregten Zuständen (Oberschwingungen)
z
z
x
y
s-AO: Drehimpuls l = 0
x
y
p-AO: Drehimpuls l = 1
30
3.5.12 Zustandsfunktionen
Quantenmechanische Zustände
Q
ΨΑ = ΨΑ(r,θ,φ) . ΨΑ(t)
ΨΒ = ΨΒ(r,θ,φ) . ΨΒ(t)
ΨC = ΨC(r,θ,φ) . ΨC(t)
Linearkombination der Zustände (Überlagerung)
Ψ = a . ΨΑ(r,θ,φ) + b .ΨΒ(r,θ,φ) + c .ΨC(r,θ,φ)
Aufenthaltswahrscheinlichkeit
Ψ2 = A2.sin2(ω.t + ϕ0)
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
4645
44
7
89
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
3.5.13 Phänomene der Wellenmechanik
• Unschärferelation Æ fundamentale Grenze der Genauigkeit der
Erfassung physikalischer Eigenschaften
• Zustandsüberlagerung (Superposition) ohne gegenseitige
Beeinflussung Æ Linearkombinationen von Wellenfunktionen
• Quantenverschränkung: räumlich getrennte Teile eines
quantenmechanischen Systems (z.B. Einzelteilchen im
Zweiteilchensystem) können unabhängig von der Entfernung
korrelierte Messwerte besitzen
Quantenmechanische Aussagen sind Wahrscheinlichkeitsaussagen !
31
3.5.14 SCHRÖDINGER Gleichung
•
•
Grundgleichung
g
g der nichtrelativistischen Quantenmechanik
zeitliche Entwicklung des Zustands eines Quantensystems
i⋅h⋅
Ψ(r,t)
m
V(r,t)
∇
•
h2
∂
Ψ (r , t ) = −
⋅ ∇ 2 Ψ (r , t ) + V (r , t ) ⋅ Ψ (r , t )
∂t
2m
= Wellenfunktion z.B. des Elektrons
= Masse z.B. des Elektrons
= Potentielle Energie z.B. des Elektrons
= Nabla-Operator
Lösung der zeitunabhängigen SCHRÖDINGERgleichung:
Energiezustände E
3.5.14.1 SCHRÖDINGERs Katze
http://de.wikipedia.org
32
3.5.15 Die Struktur der
Elektronenschalen
Hauptschalen
H
t h l nb
bestehen
t h aus U
Unterschalen
t
h l l
Die Besetzung erfolgt nach strengen Regeln
n=4
n=3
n=2
n=1
s
p
d
f
3.5.16 Die Besetzung von
Elektronenschalen
Schreibweise:
nlx
n
l
= Schalennummer
= Unterschale s,p,d,f..
x
= Zahl e- pro Orbital
Besetzungszahl, kein Exponennt !
H
He
Li
Be
B
C
N
1 s1
1 s2
1 s2
1 s2
1 s2
1 s2
1 s2
2 s1
2 s2
2 s2
2 s2
2 s2
Valenzelektronen
2p1
2p2
2p3
33
3.5.16.1 Das Pauli – Prinzip
• In einem Atom können keine zwei Elektronen in allen vier
Quantenzahlen (Hauptquantenzahl, Drehimpulsquantenzahl,
Magnetquantenzahl und Spinquantenzahl),
Spinquantenzahl) die zu seiner
Zustandsbeschreibung im Atommodell notwendig sind,
übereinstimmen.
• Als Folge des Pauliprinzips werden die Orbitale immer mit
Elektronenpaaren besetzt, die entgegengesetzten Spin
aufweisen.
3.5.16.2 Die HUNDsche Regel
• Energiegleiche Orbitale einer Unterschale werden zunächst
einfach besetzt
34
3.5.16.3 Elektronenkonfiguration
von N
PAULI Prinzip - HUNDsche Regel
E
n=3
n=2
n=1
s
p
d
Elektron mit positiver Spinrichtung
Elektron mit negativer Spinrichtung
3.5.16.4 Elektronenkonfiguration von
Na
30
11
Schreibweisen
Na
1s2 2s2 2p6 3s1
n=4
n=3
n=2
n=1
35
3.5.16.5 Das Energieprinzip
Grundzustand: werden stets
zunächst
energieärmste Orbitale
Orbitalenergien
näherungsweise
Elektroneneinbauschema
3.5.16.6 Elektronenkonfiguration
von K
Energieprinzip
E
n=4
n=3
4s
n=2
n=1
s
p
Elektron mit positiver Spinrichtung
d
Elektron mit negativer Spinrichtung
36
Welches Element ist das ?
[Ar] 3d10 4s2 4p6 = ?
?
n=4
n=3
n=2
n=1
s
p
d
f
4 Das Periodensystem der
chemischen Elemente
At
Atome
sind
i d di
die -einst
i t als
l unteilbar
t ilb geglaubtenl bt
kl i t
kleinsten
Bestandteile der der chemischen Elemente, die dessen
Eigenschaften aufweisen
Entwicklung
1829 DÖBEREINER ordnet Elemente nach Eigenschaften
1864 MEYER führt Tabellensystem ein
1869 MENDELEJEFF erstellt Urform des heutigen PS
Voraussagen über fehlende Elemente möglich
114 chemische Elemente konnte man identifizieren. Oberhalb
der Ordnungszahl 82 sind sie alle radioaktiv !
37
4.1 Systematik der
Elektronenkonfiguration
Elektronenkonfiguration
A
Anzahl
hl d
der Bi
Bindungselektronen
d
l kt
ablesbar
bl b
Wertigkeit in Molekülen erkennbar
Eigenschaften vorhersagbar
4.2 Perioden und Gruppen
Perioden
Hauptgruppen
I
II
III
IIII
V
VI
VII
VIII
1
2
1H
3Li
2He
4Be
5B
6C
7N
8O
9F
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
38
4.2.1 Hauptgruppenelemente (s,p)
I
Alkalimetalle
Li, Na, K, Rb, Cs, Fr
sehr reaktive Metalle
Erdalkalimetalle
Be, Mg, Ca, Ba, Sr, Ra
weniger reaktive Metalle
Erdmetalle
B, Al, Ga, In, Tl
Leichtmetalle
Kohlenstoffgruppe
C, Si, Ge, Sn, Pb
zunehmend metallisch
II
III
IIII
V
Stickstoffgruppe
N, P, As, Sb, Bi
zunehmend metallisch
Chalkogene
O, S, Se, Te, Po
Erzbildner
Halogene
g
F, Cl, Br, I, At
Salzbildner
Edelgase
He, Ne, Ar, Kr,Xe, Rn
innerte Gase
VI
VII
VIII
4.2.2 Nebengruppenelemente (d)
Scandium--Gruppe IIIb Sc s2p6d1
Scandium
Sc
1s2 2s2 p6
3s2 p6 d1
4s2
Y
1s2 2s2 p6
3s2 p6 d10
4s2 p6 d1
L
La
1s2 2
1
2s2 p6
3s2 p6 d10
3
4s2 p6 d10
4
5s2 p6 d1
5
Ac
1s2 2s2 p6
3s2 p6 d10
4s2 p6 d10
5s2 p6 d10
5s2
6s2
6
6s2 p6 d1
7s2
Valenzelektronen: s, d
39
4.2.3 Lanthanoide und Actinoide (f)
5d1 6s2
57La
[Xe]
58Ce
[Xe] 4f2 6s2
59Pr
[Xe]
4f3
6s2
60Nd
[Xe]
4f4
6s2
89Ac
[Rn] 6d1
7s2
90Th
[Rn] 6d2
7s2
91Pa
[Rn] 5f2
6d1 7s2
92U
[Rn] 5f3
6d1 7s2
Valenzelektronen: s, d, f
4.2.3.1 Webelements (1)
http://www.webelements.com
40
4.2.3.2 Webelements (2)
http://www.webelements.com
4.3 Die periodischen
Eigenschaften der Elemente
•
•
•
•
Atomdurchmesser
Ionisierungsenergie
Elektronenaffinität
Elektronegativität
• Gasförmige Elemente
• Flüssige Elemente
• Feste Elemente
• Radioaktive Elemente
• Metallcharakter
• Halbleitereigenschaften
41
4.3.1 Atomdurchmesser
I
II
III
IIII
V
VI
VII
VIII
1
2
1H
2He
3Li
4Be
5B
6C
7N
8O
9F
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
4.3.2 Ionisierungsenergie
Na
ΔEI
ΔEI
Na+ + eKation
.
-19
= Ionisierungsenergie = 8,3 10 J (pro Atom)
wächst mit Z
sinkt, wenn rAtom wächst
nimmt ab wie folgt: s>p>d>f
Ö
Die Ionisierungsenergie ist die Energie, die benötigt wird, um ein Atom oder Molekül
zu ionisieren, d. h. um ein Elektron vom Atom oder Molekül zu trennen
42
4.3.2.1 Ionisierungsenergie Diagramm
http://www.chemgapedia.de
4.3.2.2 Ionisierungsenergie im PS
I
II
III
IIII
V
VI
VII
VIII
1
2
1H
2He
3Li
4Be
5B
6C
7N
8O
9F
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
43
4.3.2.3 Höhere Ionisierungsenergien
Ionisierungsenergien der Elemente Z = 1, ..12
Z
Element
Ionisierungsenergie in eV zur Abtrennung des x-ten
Elektrons
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
11
12
H
He
Li
Be
B
C
N
O
F
Ne
Na
Mg
13,6
24,6
5,4
9,3
8,3
11,3
14,5
13,6
17,4
21,6
5,1
7,6
54,4
75,6
18,2
25,1
24,4
29,6
35,2
35,0
41,0
47,3
15,0
122,4
153,9
37,9
47,9
47,4
54,9
62,6
64,0
71,6
80,1
217,7
259,3
64,5
77,5
77,4
87,2
97,1
98,9
109,3
340,1
391,9
97,9
113,9
114,2
126,4
138,6
141,2
489,8
551,9
138,1
157,1
157,9
172,4
186,7
666,8
739,1
185,1
207,0
208,4
225,3
4.3.3 Elektronenaffinität
ΔEE
Cl.
+
e-
Ö
Cl-
H
F
Cl
Br
I
(kJ / mol)
- 72
-333
-364
-342
-295
Anion
ΔEE = Elektronenaffinität = - 6,0 . 10-19 J (pro Atom)
bei Halogenen besonders groß !
Die Energiedifferenz zwischen dem Grundzustand eines neutralen Atoms
und dem Grundzustand des zugehörigen Anions wird als Elektronenaffinität
bezeichnet
44
4.3.4 Elektronegativität - Bedeutung
Maßzahl:
Atom 1
EN
Bindungselektronen
Atom 2
Anziehungskraft auf Bindungselektronen
bei F am größten, bei Fr am kleinsten !
H
Fr
F
Cl
Br
I
EN
2,1
0,7
4,0
3,0
2,8
2,4
4.3.4.1 Elektronegativität Berechnung
Maßzahl:
EN
Berechnung nach Mulliken, 1966
X + eX
Æ
Æ
EN ~
XX+ + e-
ΔEE
ΔEI
1
[ΔEE + ΔEI ]
2
45
4.3.4.2 Elektronegativität im PS
I
II
III
IIII
V
VI
VII
VIII
1
2
1H
3Li
4Be
5B
6C
7N
8O
9F
2He
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
C
20Ca
G
31Ga
G
32Ge
A
33As
S
34Se
B
35Br
K
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
4.3.4.3 Elektronegativität Diagramm
F
4,5
,
Cl
4
Br
I
Ele
ektronegativit
3,5
3
2,5
2
15
1,5
1
0,5
0
1
21
41
61
81
101
Ordnungszahl
46
4.3.4.4 Die Elektronegativitätsskala
H
2,1
Li
1,0
Na
0,9
Be
1,5
Mg
1,2
K Ca
0,8 1,0
Rb Sr
0,8 1,0
Al
1,5
Sc
1,3
B
2,0
Si
1,8
C
2,5
P
2,1
Ti Ge As
1,6 1,7 2,0
Y Zr Sn Sb Te
1,3 1,6 1,7 1,8 2,1
N
3,0
S
2,5
Se
2,4
O
3,5
F
4,0
Cl
3,0
Br
2,8
I
2,4
Cs Ba
0,7 0,9
1
EN
2
3
4
4.3.5 Metallische Eigenschaften
plastisch
verformbar
elektrische
Leiter
Leitfähigkeit sinkt
mit steigender
Temperatur
relativ
große
Atomradien
Atomgitter
geringe
Ionisierungsenergie
Wärmeleiter
Supraleiter
ca. 30 metallische
Elemente
Metallglanz
47
4.3.5.1 Metallcharakter im PS
Metallcharakter
I
Nichtmetallcharakter
II
III
IIII
V
VI
VII
VIII
1
2
1H
3Li
4Be
5B
6C
7N
8O
9F
2He
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
Metalle
Halbmetalle
Nichtmetalle
4.3.6 Halbmetalleigenschaften
I
1
2
3
4
5
6
7
II
III
IIII
V
VI
VII
1H
VIII
2He
3Li
4Be
5B
6C
7N
8O
9F
10Ne
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
87Fr
88Ra
113
114
115
116
117
118
B, Si, Ge, As, Te
Leitfähigkeit steigt mit der Temperatur
mehrere Modifikationen
z.B. kristallines und amorphes Si
Halbleitereigenschaften
Elektronenleitung
Defektelektronenleitung
48
4.3.7 Dotiermittel
I
II
III
IIII
V
VI
VII
VIII
1
2
1H
3Li
4Be
5B
6C
7N
8O
9F
2He
10Ne
3
11Na
12Mg
13Al
14Si
15P
16S
17Cl
18Ar
4
19K
20Ca
31Ga
32Ge
33As
34Se
35Br
36Kr
5
37Rb
38Sr
49In
50Sn
51Sb
52Te
53I
54Xe
6
55Cs
56Ba
81Tl
82Pb
83Bi
84Po
85At
86Rn
7
87Fr
88Ra
113
114
115
116
117
118
p-type Dotiermittel
Akzeptor Atome
n-type Dotiermittel
Donator Atome
5 Das Standardmodell
49
5.1.1 Elementarteilchen und Quarks
Elementarteilchen
Leptonen
leichte Teilchen
Mesonen
gerade Anzahl von Quarks
Neutrinos
...
Baryonen
schwere Teilchen
Hyperonen
El kt
Elektronen
...
Bosonen
"Kraftteilchen"
Nukleonen
Photonen
Neutronen
Protonen
Quarks
Quarks
...
...
5.1.2 Leptonen - leichte Teilchen
Name
Symbol
Elektron
Müon
Tau
eµτ-
e+
µ+
τ+
Ruhemasse
[MeV]
0,511
105,6
1784
LadungSpin
-1 +1
-1 +1
-1 +1
mittlere
Lebensdauer [s]
1/2
1/2
1/2
stabil
2. 10-6
3. 10-13
El k
ElektronN
Neutrino
i
νe⎯νe
?
0
0
1/2
stabil
bil ?
Müon-Neutrino
νµ⎯νµ
?
0
0
1/2
stabil ?
Tau-Neutrino
ντ ⎯ντ
?
0
0
1/2
stabil ?
Leptonen + Quarks
= Grundbausteine der Materie + Antimaterie
50
5.1.3 Mesonen - Teilchen aus 2 Quarks
Name
Symbol
Pionen
π0
π+ π−
K0⎯K0
135
Kaonen
Pionen
Ruhemasse
[MeV]
Ladung
0
Quarkaufbau
Spin
mittlere
Lebensdauer [s]
u⎯u
d⎯d
0
8.10-17
u⎯d
d⎯u
0
2,6 .10-8
d⎯s ⎯d s
0
10-10 -5.10-
u⎯s
0
1,2.10-8
140
+1 -1
498
0 0
K+ K−
494
+1 -1
J / Psi
J/Ψ
3098
0
c⎯c
1
1.10-20
D-Null
D0
1863
0
c⎯u
0
1.10-12
D-Plus
D+
1863
1
c⎯d
0
4.10-13
Ypsilon
Y
9460
0
b⎯b
1
1.10-20
Kaonen
8
5.1.4 Baryonen
Name
Symbol
y
Ruhemasse
[MeV]
Proton
p ⎯p
938,3
Neutron
n ⎯n
939,6
Lambda
Λ ⎯Λ
1115
Sigma-Plus
Σ+ ⎯Σ+
1189
Sigma-Minus
Σ− ⎯Σ−
1197
Sigma-Null
Σ0 ⎯Σ0
1192
Xi-Minus
Ξ− ⎯Ξ−
1321
Xi-Null
Ξ0 ⎯Ξ0
1315
−
−
Omega-Minus Ω ⎯Ω
1672
Charm-Lambda Λc ⎯Λc
2280
- schwere Teilchen
Ladung
g
+1
0
0
+1
-1
0
-1
0
-1
+1
s⎯u
-1
0
0
+1
-1
0
1
0
-1
+1
Quarkaufbau Spin
Q
p mittlere
Lebensdauer [s]
u u d ⎯u⎯u⎯d ½
stabil
d d u ⎯d⎯d⎯u ½
ca. 900
u d s ⎯u⎯d⎯s ½
2,6.10-10
u u s ⎯u⎯u⎯s ½
8.10-11
d d s ⎯d⎯d⎯s ½
1,5.10-10
u d s ⎯u⎯d⎯s ½
6.10-20
d s s ⎯d⎯s⎯s ½
1,6.10-10
u s s ⎯u⎯s⎯s ½
3.10-10
s s s ⎯s⎯s⎯s ½
8.10-11
u d c ⎯u⎯d⎯c ½
2.10-13
51
5.1.5 Eichbosonen
Name
Symbol
Photon
W-Teilchen
Z-Teilchen
Gluon
γ
W + W−
Z
g
Ruhemasse
[MeV]
- Austauschteilchen
Ladung
?
~83 000
~93 000
0
Spin
0
1
0
0
mittlere
Lebensdauer [s]
1
-1
1
1
stabil
10-25
10-25
stabil
Austauschteilchen, übertragen Kräfte
5.1.6 Quarks
- Bausteine für Elementarteilchen
Name
Symbol
up
down
strange
charm
bottom (beauty)
top (truth)
u ⎯u
d ⎯d
s ⎯s
c ⎯cc
b ⎯b
t ⎯t
Ruhe
Ruhemasse
[MeV]
~5
~10
~100
~1500
1500
~4700
?
Ladung
2/3
- 2/3
-1/3
-1/3
1/3
2/3
-2/3
1/3
-1/3
1/3
2/3
-2/3
Spin
mittlere
Lebensdauer [s]
½
½
½
½
½
½
stabil
verschieden
verschieden
verschieden
verschieden
verschieden
Elementarteilchen aus Quarktripletts : Baryonen
Elementarteilchen aus Quarkdubletts: Mesonen
52
5.1.6.1 „Visual“- Quarks
top
up
down
bottom
strange
charm
6 Nuklidkarte
In der Nuklidkarte werden alle Atomarten (Nuklide) nach Protonenund Neutronenzahl geordnet.
Aus der Nuklidkarte lassen sich Eigenschaften der Nuklide
ablesen, z.B. Stabilität oder radioaktive Zerfallsarten
53
6.1 Nuklidbegriff
Atome
Die stoffliche Welt um uns herum lässt sich zerlegen in kleine einst als unteilbar geglaubte - Teilchen, die als Atome bezeichnet
werden.
Nuklide
Zur Zeit sind ca. 2500 Atomsorten - sogenannte Nuklide - bekannt,
die sich auf 115 verschiedene chemische Elemente verteilen
verteilen.
Davon sind nur 274 Nuklide stabil !
Chemische Elemente
Unter einem chemischen Element versteht man einen Stoff, der
aus Atomen mit gleichen chemischen Eigenschaften aufgebaut ist.
6.1.1 Schreibweisen
Nukleonenzahl
Ordnungszahl
Schreibweise:
Neutron
Proton
Nukleonenzahl
Element
Ordnungszahl
Element
1
1
1
H
1
4
2
4
He
2
12
6
12
C
6
54
6.1.2 Bekannte Nuklide
radioaktiv
• C-14
• I-131
• Tc-99
• Cs-137
• U-235
• U-238
aus der Radiocarbonmethode
aus der Radiojodtherapie
aus aus der Radiologie / Szintigraphie
aus dem Reaktorunfall von Tschernobyl
aus dem Kernbrennstoff
aus dem Kernbrennstoff
stabil
• C-12
• B-10
• H-2
aus der Radiocarbonmethode
aus der Nukleartechnik
aus der Nukleartechnik
6.2 Nuklidkarte
Isotope
p Nuklide
weisen die gleiche Ordnungszahl auf und gehören damit zum
selben chemischen Element.
He
He-3
He-4
He-5
He-6
4,002602
0,000137
99,99986
99,99986
806,7 ms
3β− 0,02
n
σabs < 0,05
σ 0,00005
H
H-1
H-2
H-3
1,00794
99,985
0,015
12,323 a
σ 0,332
σ 0,332
σ 0,00052
β- 3,5
Z
β− 0,02
n1
10,25 m
β− 0,8
N
55
6.2.1 Nuklidkarte FZ Karlsruhe
6.2.1.1 Nuklidkarte Erläuterungen
Karlsruher Nuklidkarte: alle bekannten Nuklide
X - Achse: Neutronenzahl
Y - Achse: Protonenzahl
Farben und Symbole:
stabile Nuklide
Positronzerfall
β+
Elektroneneinfang
ε
Negatronzerfall
β-
Alphazerfall
α
Spontanspaltung
sf
Protonzerfall
p
Isomerenzerfall
Iγ
56
6.2.2 Nuklidkarte TOICD (1)
6.2.2.1 Nuklidkarte TOICD (2)
57
6.3 Zerfallsreihen
•
Zerfallsreihe: Abfolge
g des radioaktiven Zerfalls, die entsteht, wenn ein
radioaktives Nuklid seinerseits in ein anderes radioaktives zerfällt
(Isotopenfolge). Da die natürlichen Zerfallsarten die Massenzahl des
Nuklids entweder unverändert lassen, wie die Gamma- und
Betastrahlung oder um vier vermindern, wie die Alphastrahlung, gibt es
für schwere natürliche Radionuklide vier verschiedene Zerfallsreihen:
Uran-Radium-Reihe:
Uran-Actinium-Reihe:
Uran
Actinium Reihe:
Thorium-Reihe:
Neptunium-Reihe:
•
Ausgangsnuklid U-238
Ausgangsnuklid U
U-235
235
Ausgangsnuklid Th-232
Ausgangsnuklid Np-237
Endnuklid Pb-206
Endnuklid Pb
Pb-207
207
Endnuklid Pb-208
Endnuklid Bi-209
Die 4. Zerfallsreihe kommt in der Natur nicht vor, da das langlebigste
Glied 237Np dieser Reihe praktisch vollständig zerfallen ist.
http://de.wikipedia.org
6.3.1 Die Uran-Radium-Zerfallsreihe
U-238
Th-234
Pa-234
U-234
Th-230
Ra-226
Rn-222
Po-218
α
β−
α
Pb-214
β− Bi-214
α Tl-210 β−
α Pb-210
α
Hg-206
β−
Tl-206 β−
Pb-206
α
β−
β−
α
α
α
α
β−
α
β−
α
At-218
Rn-218 β−
Po-214 α
Bi-210 β−
Po-210
58
6.3.2 Die Uran-Actinium-Zerfallsreihe
Th-227
Pb-211
Po-211
U-235
U
235
Th-231
Pa-231
β− Ac-227
α
α
α
α
β−
β−
α
Ra-223
Rn-219
Po-215
Bi-211
Pb-207
α
β−
α
α
β−
β−
β−
β−
α
α
β−
Fr-223
α
At-219
α
Bi-215
At-215
Tl-207
6.3.3 Die Thorium-Zerfallsreihe
β−
Po-212 α
Th 232
Th-232
Ra-228
Ac-228
Th-228
Ra-224
Rn-220
Po-216
Pb-212
Bi-212
Pb-208
α
β−
β−
α
α
α
α
α
β−
β− Tl-208
59
6.3.4 Die Plutonium-NeptuniumZerfallsreihe
β−
α
Pu-241
Pu
241
Am-241
Np-237
Pa-233
U-233
Th-229
Ra-225
Ac-225
Fr-221
At-217
Bi-213
Tl-209 β−
Pb-209
Bi-209
α
U-237
α
α
β−
α
α
β−
α
α
β−
α
Rn-217 α
Po-213
β−
6.4 Nuklidgruppen
Isotope Nuklide
weisen die gleiche Ordnungszahl auf und gehören damit zum
selben chemischen Element
Isobare Nuklide haben gleiche Massen, jedoch unterschiedliche
Kernladungszahlen. Sie finden sich in den Diagonalreihen der
Nuklidkarte.
Isotone Nuklide sind Nuklide mit gleicher Neutronenzahl
Neutronenzahl. Sie
stehen in den senkrechten Reihen der Nuklidkarte.
Isomere Nuklide haben zwar gleiche Anzahl von Protonen und
Neutronen, besitzen aber unterschiedliche Energien im
Atomkern.
60
6.5 Wasserstoffisotope
1
1
2
1
3
1
T
7 Anti-Materie
• Zu jedem Teilchen gibt es ein Anti-Teilchen
(gleiche Masse, aber entgegengesetzte Ladung)
Anti Teilchen in
• Tritt ein Teilchen mit seinem Anti-Teilchen
Wechselwirkung, so werden beide vernichtet, es
entstehen Photonen oder Mesonen
• Das Photon ist mit seinem Anti-Teilchen identisch
61
8 Radioaktivität
Eigenschaft bestimmter Stoffe, sich ohne äußere Einwirkung
umzuwandeln und dabei charakteristische Strahlung
auszusenden
Alpha-Zerfälle
Beta-Zerfälle
Gamma Zerfälle
Gamma-Zerfälle
Röntgenstrahlung
Spontanspaltung
Spallation
u.a.
Aussenden von He2+ - Teilchen
Aussenden von e-,e+ aus dem Kern
Aussenden von Photonen aus dem Kern
Aussenden von Photonen aus inneren
Elektronenschalen
Spaltung eines Atomkernes
Zertrümmerung eines Atomkernes
8.1 Aktivität
Aktivität = Anzahl der Zerfälle pro Sekunde
1 Becquerel = 1 Zerfall pro Sekunde
Symbol : Bq
1 Gramm Radium-226: 37 Milliarden Zerfälle pro Sekunde
37 Milliarden Bq = 1 Curie (Ci)
62
8.1.1 Die natürliche Aktivität
eines Standardmenschen
Radionuklid
Aktivität in Bq
K - 40
4 500
C -14
3 800
Rb - 87
650
Pb - 210, Bi - 210, Po - 210
60
Daughters
g
Rn - 220
30
H-3
25
Be - 7
25
Daughters Rn - 222
15
Sonstige
7
Summe
9 112 (ca. 130 Bq / kg)
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
8.1.2 Spezifische Aktivität in
Nahrungsmitteln
Stoff
Aktivität in Bq / kg
KCl
vegetarische Nahrungsmittel
Rentierleber (Po
(Po-210)
210)
Paranüsse (Ra- 226)
15 944
40*
222
132
* Mittelwert
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
63
8.1.3 Aktivität eines Frühstücks
Nahrungsmittel
120 g Mischbrot
25 g Camenbert
25 g Corned Beef (Jugoslawien)
20 g Nuß-Nougat-Creme
125 ml schwarzer Tee (Türkei)
Aktivität in Bq
2,0
0,9
1,2
3,2
6,5
Ni ht
Nicht
verkehrsfähig !
100 g Quark
25 g Blaubeeren
0,2
2,4
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
8.1.4 Aktivität eines Mittagessens
Nahrungsmittel
150 g Wildfleisch (Niedersachsen)
60 g Nudeln, gekocht
200 g Maronen (Niedersachsen)
Aktivität in Bq
87,2
0,6
210,6
Nicht
verkehrsfähig !
20 g Pfirsich (Konserve, Griechenland)
10 g Preisselbeermus (Skandinavien)
150 g Vanilleeis
50 g Kirschen
1,0
0,0
3,0
16,7
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
64
8.2 Der radioaktive Zerfall
A
A
t½
t
Aktivität
Halbwertszeit
vergangene Zeit
exponentieller Zerfall
t
t½
Unter Halbwertszeit eines Radionuklids versteht man die
Zeit, in der seine Aktivität auf die Hälfte abgeklungen ist
8.2.1 Das Zerfallsgesetz
A(t )= A0 ⋅ e
A(t)
t
A0
t½
− ln 2 .
t
t1 / 2
= Aktivität nach einer Zeit t
= vergangene Zeit
= Aktivität am Anfang ( t = t0)
= Halbwertszeit
65
Übung zum J-131- Zerfall
Iod-131 hat eine Halbwertszeit von 8 Tagen
Wieviel Bq sind nach 16 Tagen messbar, wenn zum Zeitpunkt t0
die Aktivität 100 000 Bq betrug ?
?
Übung zum Cs-137 - Zerfall
Beispiel
p Cs-137
t1/2 = 30 y
A(0) = 1 GBq für t= 0
A(30 y) = ?
?
66
8.2.2 Alpha-Zerfall
226
88
Ra →
222
86
Rn +
4
2
He (4,601 MeV ) + γ (0,186 MeV ) 5,5 %
226
88
Ra →
222
86
Rn +
4
2
He (4,784 MeV )
94,4%
8.2.2.a Alpha-Zerfall
Äußere Bestrahlung unbedeutend
Abschirmung durch Papier
Inkorporation gefährlich
67
8.2.2.1 Alpha-Strahlung
• Teilchenart
• Radionuklide
• Energie
• Reichweite
• Energieabgabe
• Wechselwirkung
• Gefahren
• Schutz
He- 4 Kerne
Z> 80: Pu - 239, Ra - 226, Rn - 222,
Am - 241, Po - 210, U - 235
MeV
bei 5 MeV ca. 3,5 cm (Luft)
der größte Anteil wird auf einmal
abgegeben
Ionisation, Anregung
Inkorporation,
Schleimhäute
Abschirmung mit Papier,
Abstand > 10 cm
8.2.2.2 Alpha-Zerfallsschema
http://atom.kaeri.re.kr/cgi-bin/decay?Ra-226%20A
68
8.2.2.3 Absorption von αStrahlung
Ionenpaaare pro cm
2000 4000 6000
Ionisation umgebender
g
Materie
Streuung bei kleinen Teilchenenergien um kleine Winkel
Reichweite schwergeladener Teilchen ≈ Länge der Teilchenbahn
1
2 3 4 5 6
Wegstrecke [cm]
7 8
He + + + 2e − → He
8.2.3 Beta-Zerfall
+υ
+υ
137
55
Cs →
137
56
Ba +
0
−1
e
69
8.2.3a Beta-Zerfall
Äußere Bestrahlung von untergeordneter Bedeutung
Abschirmung durch Plexiglas, Aluminium
8.2.3.1 Beta-Strahlung
• Teilchenart
• Radionuklide
•
•
•
•
Energie
Reichweite
Energieabgabe
Wechselwirkungen
• Gefahren
• Schutz
Negatronen, Positronen
Negatronen
H - 3, C - 14, Sr - 90, Cs - 137
Tl - 204, Co - 60
keV ... MeV
bei 1 MeV ca. 4 m (Luft)
kontinuierlich
Ionisation, Anregung,
Bremsstrahlung
Streustrahlung,
Hautexposition, Schleimhäute
Inkorporation
Abschirmung mit Al, PMMA
70
8.2.3.2 Beta- Zerfallsschema
http://atom.kaeri.re.kr/cgi-bin/decay?Cs-137%20B-
8.2.3.3 Energie von Beta-Strahlung
Betateilchen besitzen ein Energiespektrum
g p
beim Betazerfall entstehen Neutrinos (ν)
Zerfallsenergie verteilt sich auf Betateilchen und Neutrinos
E
Relative Häufigkeit
20 40 60 80 100
Häufigste Energie
1
E ≈ Emax
3
MaximaleEEnergie
max
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8
Energie [MeV]
71
8.2.3.4 Absorption von β Strahlung
Ionisation und Anregung umgebender Materie
Streuung
Bremsstrahlung
Ionenpaare pro cm (β) = 10-2 – 10-3 • Ionenpaare pro cm (α)
Reichweite (α) in Luft: cm
Reichweite (β) in Luft: cm – m
α-Strahlung: dicht ionisierend
β-Strahlung locker ionisierend
8.2.4 Gamma-Zerfall
137 m
56
Ba →
137
56
Ba + γ
72
8.2.4.a Gamma-Zerfall
Äußere Bestrahlung maßgeblich
Abschirmung durch Blei
8.2.4.1 Gamma-Strahlung
• Teilchenart
• Quellen
•
•
•
•
Energie
Reichweite
Energieabgabe
Wechselwirkungen
• Gefahren
• Schutz
Photonen
Am - 241, Co - 60, I - 131,
Ba - 133, Ba - 137m, Tc - 99m
keV ... MeV
theoretisch ∞
paketweise
Streuung,
Photoeffekt,
Comptoneffekt,
Paarbildungseffekt
Körper-Exposition,
Inkorporporation
Abschirmung mit Pb
73
8.2.4.2 Gamma-Zerfallsschema
http://atom.kaeri.re.kr/cgi-bin/decay?Cs-137%20B-
8.2.4.3 Absorption von γ -Strahlung
Mechanismen zur Absorption von Photonen:
Photoeffekt bei kleinen Photonen-Energien
(vollständige Absorption in der Atomhülle)
Comptoneffekt bei mittleren Photonen-Energien
(inkohärente Streuung in der Atomhülle)
Paarbildungseffekt bei großen Photonen-Energien
(vollständige Absorption im COULOMB-Feld des Atomkerns)
Abhängig von der Dichte des Mediums !
74
8.2.4.4 Photo-, Compton- und
Paarbildungseffekt
8.2.4.5 Photoeffekt
Einfallendes
Photon
Photoelektron
σ Photo ~
Z5
E7/2
σ Wirkungsquerschnitt Z Ordnungszahl E Photonenenergie
75
8.2.4.5.a Photoeffekt - animiert
8.2.4.6 COMPTON effekt
Gestreutes
Ph t
Photon
Einfallendes
Photon
COMPTON elektron
E << me ⋅ c 2
σ COMPTON ( E , Θ) ~ const
E >> me ⋅ c 2
σ COMPTON ( E , Θ) ~
1
E
σ Wirkungsquerschnitt Z Ordnungszahl E Photonenenergie
θ Einfallswinkel
76
8.2.4.6.a COMPTON effekt animiert
8.2.4.7 Paarbildungseffekt
Einfallendes
Photon
Positron
Elektron
E > 1,022 MeV
σ Paar ~ Z 2
σ Wirkungsquerschnitt Z Ordnungszahl E Photonenenergie
77
8.2.4.7.a Paarbildungseffekt animiert
8.2.5 Beispiele für Zerfälle
Radionuklid
Häufigkeit
Zerfallsart
Halbwertzeit t1/2
Tritium
Ra - 226
I - 131
Cs - 134
0,00013 %
βα/γ
β- / γ
β/γ
U - 235
U - 238
0,720 %
99,28 %
12,346
1,6 . 103
8,04
2,06
2,09
7,030 . 108
4,468 . 109
α, γ, sf *
α, γ, sf
a
a
d
a
h
a
a
* sf bedeutet spontaneous fission = Spontanspaltung
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
78
8.3 Strahlungsenergie
1 J = 1 Nm = 1 Ws
1 eV ist die Energie, die ein Elektron aufnimmt, wenn es beim
f i D
freien
Durchlaufen
hl f einer
i
S
Spannung von 1 V b
beschleunigt
hl
i t wird
id
1 eV = 1,602 •10-19 J
8.3.1 Energieeinheiten
Energieeinheiten
J
eV
kWh
cal
erg
kg
u
Joule
1 J = 1 N.m
Elektronenvolt
Kilowattstunde
1 W = 1 kg.m2/s3 = 1 J/s
Kalorie
Energieeinheit
Kilogramm
atomare Masseneinheit
79
8.3.2 Umrechnungsfaktoren
1J
J
MeV
kWh
cal
erg
kg
1
6,250E+12
2,778E-07
2,389E-01
1,000E+07
1,113E-17
1 MeV
1,600E-13
1
4,450E-20
3,827E-14
1,602E-06
1,783E-30
1 kWh
3,600E+06
2,247E+19
1
8,600E+05
3,600E+13
4,007E-11
1 cal
4,186E+00
2,613E+13
1,163E-06
1
4,168E+07
4,660E-17
1 erg
1,000E-07
6,242E+05
2,778E-14
2,389E-08
1
1,113E-24
1 kg
8,985E+16
5,610E+29
2,497E+10
2,146E+16
8,987E+23
1
1u
1,492E-10
9,320E+02
4,146E-17
3,546E-11
1,492E-03
1,661E-27
Quelle: Halliday, Resnik, Walker - Physik, Wiley-VCH Verlag
8.4 Strahlendosis: Energiedosis
Energiedosis D = absorbierte Energie
Definition:
Energiemenge, die durch die Strahlung auf eine Masseneinheit
1J
übertragen
1 Gray = wird
kg
Symbol: Gy
Alte Einheit: rad (1 Gy = 100 rad)
80
8.5 Strahlendosis: Personendosis
Äquivalentdosis
Ä
i l td i H = Z
Zellschädigung
ll hädi
durch absorbierte Energie
H = D ⋅Q
Definition:
Sievert
Energiemenge die auf einen Menschen übertragen wird
Energiemenge,
wird, abhängig von
der Strahlenart
Symbol: Sv
Alte Einheit: rem (1 Sv=100 rem)
H = Personendosis D = Energiedosis Q = Qualitätsfaktoren für Strahlungs- und Gewebeart
8.6 Dosisleistung
Unter der Dosisleistung DL versteht man die mit der Zeit
aufgenommene (Strahlen)dosis
DL =
dD •
=D
dt
DL =
•
dH
=H
dt
DL = Dosisleistung D = Energiedosis H = Äquivalentdosis t = Zeit
81
8.6.1 Das Abstandsgesetz
Dosisleistung
g einer p
punktförmigen
g γγ-Strahlungsquelle
g q
dH
A
H& =
= ΓH ⋅ 2
dt
r
dH/dt
ΓH
A
r
Nuklid
ΓH
Co-60
Cs-137
I-131
351
88
59
⎡ µSv ⋅ m 2 ⎤
⎢
⎥
⎣ GBq ⋅ h ⎦
= Gammadosisleistung
= Gammadosisleistungskonstante (tabelliert)
= Aktivität
= Abstand zur Strahlungsquelle
Dosisleistung eines Cs-137
Strahlers
Beispiel
p Cs-137
A = 1 GBq
r = 10 m
Dosisleistung = ?
?
82
8.7 Strahlenschutz
Abstand
Abschirmen
Aufenthalt
Quelle: Volkmer – Rad
diaoaktivität und Strahlenschu
utz
8.8 Strahlenbelastungen
Mean Effective Dose Rate [mSv/a]
cosmic radiation
terrestric radiation
internal natural exposure
total natural
medical application
industrial activities
Tschernobyl
nuclear weapon tests
flights
working environment
fossile energy
nuclear energy
industrial products
total civilisation
Total
0,3
0,4
1,4
2,1
2
0,01
0,01
0 005
0,005
0,005
0,002
0,002
0,001
0,001
2,036
4,136
83
8.8.1 Terrestrische Strahlung
Area
Anual Dose Mean
Anual Dose Maximum
[mSv/a]
0,4
[mSv/a]
5
4
55
6
6
175
860
Germany
Kerala, Tamil,
Nadu (India)
Espirito Santo
(Brasilia)
Ramsar (Iran)
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
Dosisleistung [mSv/a]
0,5
1,0 1,5 2
8.8.2 Kosmische Strahlung
f
e
cd
1
2
3
4
5
Höhe über Meeresspiegel [km]
c Hamburg d München e Zugspitze f Großglockner
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
84
8.8.3 Natürliche
Strahlenexposition
Effective Dose Rate [mSv/a]
external
internal
total
cosmic
1000 m above sea level
0 m above sea level
radio nuclides
0,4
0,27
0,02
0,4
0,27
0,02
0,35
0,006
1,29
0,22
1,89
terrestric
K-40
Rb-87
U-nat
Th-nat
0,12
0,14
0,17
0,006
1,17
0,08
Σ
0,71
1,45
0,18
Total
2,16
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
8.8.4 Beispiele für Äquivalentdosen
7000
4000
1000
250
200
0,01
20
6
0,3
2,0
mSv
mSv
mSv
mSv
mSv/a
mSv
mSv/a
mSv/a
mSv/a
mSv/a
2,1 mSv/a
<3 mSv/a
Strahlentod LD100
Schwere Strahlenkrankheit LD50
"Strahlenkater„
Schwellendosis (erste klinische Effekte)
Maximale natürliche Strahlenbelastung (Brasilien, Monazit)
3 h Flug 10 km Höhe
Grenzwert für berufliche Strahlenbelastung (Kategorie A)
Grenzwert für berufliche Strahlenbelastung
g ((Kategorie
g
B))
Grenzwert für Belastung aus kerntechnischen Anlagen
Mittlere Strahlenbelastung durch medizinische
Anwendungen
Mittlere natürliche Strahlenbelastung D
Zusätzliche natürliche Strahlendosis
(Beton-, Granitbauten)
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
85
8.8.5 Strahlenbelastung beim
Fliegen
Effektive Dosis durch Höhenstrahlung
g auf ausgewählten
g
Flugrouten
g
Abflug
Ankunft
Dosisbereich* [µSv]
Frankfurt
Frankfurt
Frankfurt
Frankfurt
Frankfurt
Frankfurt
Frankfurt
Gran Canaria
Johannesburg
New York
Rio de Janeiro
Rom
San Francisco
Singapur
10 - 18
18 - 30
32 - 75
17 - 28
3-6
45 - 110
28 - 50
* Die Schwankungsbreite geht hauptsächlich auf die Einflüsse von
Sonnenzyklus und Flughöhe zurück.
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
8.8.6 Strahlenbelastung bei der
Raumfahrt
Flug
Erdumkreisung
Erdumkreisung
Mondumkreisung
Mondlandung
Mondlandung
APOLLO VII
SALJUT 6 / IV
APOLLO XI
APOLLO XI
APOLLO XIV
Flugdauer [h]
Dosis [mSv]
260
4 200
147
195
209
3,6
55
5,7
6
15
Quelle: Volkmer – Radiaoaktivität und Strahlenschutz
86
9 Kernphysik
H-2 + He-3 Æ He-4 + p + 18,35 MeV
Energieerzeugung durch Kernfusion (fusion)
n + U-235 Æ Cs-137 + Rb-96 + 3n + 210 MeV
Energieerzeugung durch Kernspaltung (fission)
Bildquelle: Forschungszentrum Karlsruhe
9.1 Nukleonenmassen
Nukleon
Masse
[g]
Proton 1,672 x 10-24
24
N
Neutron
1 6 4 x 10-24
1,674
Relative
Ladung Spin
t1/2
Atommasse
Betazerfall
[u]
1,00728
1,00867
1
0086
+e
0
½
½
stabil
12 min
i
1 u = 1,660 x 10-24 g = 931,5 MeV
87
9.2 Massendefekt
Als Massendefekt bezeichnet man die Differenz zwischen den
Ruhemassen gebundener Nukleonen und den Ruhemassen
ungebundener Nukleonen.
Der Massendefekt ist ein Maß für die Kernbindungsenergie.
Massendefekt eines Alphateilchens:
Δm = malpha
Δm = 4,00151
= 0,0307u
≅ 28 MeV
- (2 x mproton
+ 2 x mneutron)
- (2 x 1,00782 + 2 x 1,00866)
9.3 Kernbindungsenergien
Mittlere
tt e e Kernbindungsenergie
e b du gse e g e p
pro
o Nukleon
u eo
Massenzahl
88
9.4 Kernfusion
Unsere Sonne wandelt in 1 s ca. 600 Millionen Tonnen Wasserstoff in 596
Millionen Tonnen He um
Æ 4 Millionen Tonnen Materie werden in Energie umgewandelt !
9.6 Die 4 fundamentalen Kräfte
• Elektromagnetische Kraft
Anziehung/Abstoßung von
Ladungsträgern (Reichweite: ∞)
• Gravitationskraft
Anziehung von Massen
(Reichweite: ∞)
• Starke Kernkraft
bindet Nukleonen
(ca. 2,0 x 10-13 cm Reichweite)
• Schwache Kernkraft
bindet Quarks
verursacht radioaktiven Beta-Zerfall
(ca. 0,5 x 10-13 cm Reichweite)
89
9.7 Kernspaltung
Kernspaltung
9.7.1 Nukleare Kettenreaktion
90
9.7.2 Spaltproduktausbeute
Ausbeute
bei Spaltung
von U-235
Massenzahl
9.8 Kernreaktionen
Einfang von e-, He++
0
−1
e +
→
40
19
K
40
18
Ar
Einfang von Neutronen
1
0
n +
B →
10
5
Li +
7
3
He + γ
4
2
91
9.8.1 Künstliche Kernreaktion
Reaktion von α-Strahlen mit Stickstoff
14N(α,p)17O
4
2
He +
14
7
N
→
18
9
F
→
O +
17
8
1
1
p
9.8.2 Der Bethe-Weizäcker-Zyklus
Kohlenstoff-Stickstoff-Zyklus
Bethe-Weizsäcker-Zyklus
12C
+ 1H
13N
13C
14N
+ 1H
+ 1H
15O
15N
+ 1H
→
→
→
→
→
→
13N
+γ
13C + e+ + ν
e
14N + γ
15O + γ
15N + e+ + ν
e
12C + 4He
+ 1,95 MeV
+ 1,37 MeV
+ 7,54 MeV
+ 7,35 MeV
+1
1,86
86 MeV
+ 4,96 MeV
Lebensdauer
1,3·107 Jahre
7
Minuten
2,7·106 Jahre
3,2·108 Jahre
82
Sekunden
1,12·105 Jahre
Energiequelle der schwereren Sterne ! Durchlauf des Zyklus: 3,4·108 Jahren
Die Energieerzeugungsrate ist beim Bethe-Weizsäcker-Zyklus proportional zur
15. Potenz der Temperatur
http://de.wikipedia.org
92
9.8.3 Die Proton-Proton-Reaktion
1H
+ 1H
e+ + e2H + 1H
3He +3He
→
→
→
→
2H
+ e+ + νe
2γ
2
3He + γ
4He + 1H + 1H
3He
+ 4He →
+ e→
7Li + 1H
→
7Be
7Be
7Li
3He
7Be
7Be
8B
+ 4He →
+ 1H
→
8B
→
8Be
↔
+ 0,42 MeV
+ 1,02
1 02 MeV
M V
+ 5,49 MeV
+ 12,86 MeV
+γ
+ νe
4He + 4He
+γ
+γ
8Be + e+ + ν
e
4He + 4He
10–14 Millionen Kelvin
14–23 Millionen Kelvin
>23 Millionen Kelvin
Die „Asche“ des Wasserstoffbrennens ist Helium 4He
bei Sternen mit Größen bis zur Masse der Sonne
http://de.wikipedia.org
10 Kernreaktoren
• Leistungsreaktoren
– Druckwasserreaktoren
– Siedewasserreaktoren
– Schneller Brüter
– Thorium Hochtemperatur Reaktor
• Forschungsreaktoren
– Neutronenquellen
– Unterrichtsreaktoren
– ....
93
10.1 Druckwasserreaktor
http://www.kernenergie.de
10.2 Siedewasserreaktor
http://www.kernenergie.de
94
10.3 RBMK Reaktor
http://www.kernenergie.de
10.4 Sicherheit im KKW
http://www.kernenergie.de
95
10.5 Brennelemente
Ein Brennelement eines
Druckwasserreaktors
530 kg Uran
Ein Brennelement eines
Siedewasserreaktors
190 kg Uran.
Druckwasserreaktor des
Kernkraftwerks Emsland
193 Brennelemente
Siedewasserreaktor des
Kernkraftwerks Krümmel
840 Brennelemente
http://www.kernenergie.de
10.6 Brennelementzyklus
http://www.kernenergie.de
96
10.7 SUR-100 Reaktor
10.8 Actinidenelemente
http://www.kernenergie-wissen.de/transmutation.html
jährlich von einem typischen Druckwasserreaktor bei 3.0 GW produziert
Nuklide
kg/Jahr
Halbwertszeit/in Jahren
Pu-238
4.52
88
Pu-239
166
2.4 x 104
Pu-240
76.7
6.6 x 103
Pu-241
25.4
14.4
Pu-242
15.5
3.8 x 105
Np-237
14.5
2.1 x 106
Am-241
16.6
432
Am-242m
0.022
141
Am-243
2.99
7.4 x 103
Cm-243
0.011
28.5
Cm-244
0.58
18.1
ber. nach 10 a Lagerung u. typischen Abbrand von 33'000 MWtagen per Tonne Uran
97
10.9 Transmutation
Umwandlung
g von langlebigen
g
g Radionukliden in kurzlebige
g
Np-237, Pu-238, Pu-239, Pu-240, Am-241, Am-243, Cm-243, Cm-244
in abgebrannten Brennelementen erfordern den Nachweis der
Sicherheit der Lagerung über sehr lange Zeiträume
• die Anregung des Nuklids mit anschließenden Betazerfällen
(Umwandlung von Neutronen in Protonen oder umgekehrt)
• die Anregung des Nuklids mit anschließendem Abdampfen von
Neutronen, Protonen, Alpha-Teilchen usw.
• die Spaltung des Nuklids in zwei oder drei große Tochternuklide
• die Zertrümmerung des Nuklids (Spallation) in viele kleine Nuklide
11 Radioaktive Abfälle
• Entstehung
• Klassifizierung nach
Aktivität
• Klassifizierung nach
Wärmeentwicklung
• Zwischenlagerung
• Endlagerung
• Wiederaufbereitung von
Kernbrennstoff
www.kernenergie.de
98
11.1 Entstehung
Nukleare Prozesse
• Aktivierung
• Spaltprodukte
Medizin, Forschung, Industrie
• Prüfstrahler
• Kontaminierte Gegenstände
Uranbergbau
Militär
11.2 Klassifizierung nach Bq
• schwachaktiv (LAW: low active waste)
> 1010 Bq/m3
• mittelaktiv (MAW: medium active waste)
1010 Bq/m3 - 1014 Bq/m3
• hochaktiv (HAW: high active waste)
> 1014 Bq/m3
90 %
270 000 m3
10 %
24 000 m3
www.kernenergie.de
99
11.3 Klassifizierung nach
Wärmeentwicklung
Abfälle mit nicht vernachlässigbarer
g
Wärmeentwicklung
g
> 3 Kelvin
Abfälle mit vernachlässigbarer Wärmeentwicklung
< 3 Kelvin
31.12.2005 waren insgesamt ca. 117.350 m³ radioaktive Reststoffe
mit vernachlässigbarer Wärmeentwicklung und ca. 1.850 m³
wärmeentwickelnde radioaktive Reststoffe vorhanden. In dem o. g.
B t d am 31.12.2005
Bestand
31 12 2005 an wärmeentwickelnden
ä
t i k l d Abfäll
Abfällen sind
i d
außer den ausgedienten Brennelementkugeln des ThoriumHochtemperaturreaktors (THTR) keine abgebrannten
Brennelemente aus Leistungsreaktoren enthalten. Die THTRBrennelementkugeln wurden vom Betreiber als Abfall deklariert
und erscheinen deshalb in der Abfallstatistik.
www.kernenergie.de
11.4 Zwischenlager
Zur Zeit werden abgebrannte Brennelemente entweder in die beiden zentralen
Zwischenlager nach Ahaus (Nordrhein-Westfalen) und Gorleben
(Niedersachsen) oder zur Wiederaufarbeitung in ausländische Anlagen
transportiert. Um diese Transporte zu minimieren, soll nun auf Wunsch der
Bundesregierung zusätzlich die Möglichkeit geschaffen werden, abgebrannte
Brennelemente am Kraftwerksstandort zwischen zu lagern. Hierzu sollen
Standortzwischenlager errichtet werden, die die Brennelemente bis zu ihrer
Einlagerung im Endlager in 30 bis 40 Jahren aufnehmen können. Von den
Betreibern der Kernkraftwerke wurden beim Bundesamt für Strahlenschutz
Genehmigungsanträge zur Errichtung von Standortzwischenlagern gestellt.
Für die Zwischenlagerung werden die Brennelemente in spezielle
Transport/Lager-Behälter (Castor®-Behälter) verpackt, die sowohl zum
Transport vom Kernkraftwerk zum Zwischenlager als auch als Lagerbehälter
dienen. Die 40 cm starke Wandung schirmt die Strahlung ab, an der
Außenseite des Behälters angebrachte Kühlrippen gewährleisten eine
sichere Wärmeabgabe der durch den Zerfall der Spaltprodukte entstehenden
Wärme an die Umgebungsluft.
www.kernenergie.de
100
11.5 Endlager
Wartungsfreie, zeitlich unbefristete und sichere Beseitigung von radioaktivem Abfall ohne beabsichtigte Rückholbarkeit. In Deutschland wird die Lagerung radioaktiver Abfälle in tiefen geologischen
Formationen als die beste Lösung angesehen. Folgende Endlager
sind genehmigt, werden untersucht oder waren in Betrieb:
Schachtanlage Konrad
Salzstock Gorleben
Salzbergwerk Asse
Morsleben (ERAM)
www.kernenergie.de
11.5.1 Schachtanlage Konrad
Die am 5. Juni 2002 für die Schachtanlage Konrad
erteilte Genehmigung zur Endlagerung von radioaktiven Abfällen (ca. 300.000 Kubikmeter), die eine
vernachlässigbare thermische Einwirkung auf das
umgebende Gestein haben, ist mit der am
03.04.2007 erfolgten Beschlussfassung des Bundesverwaltungsgerichts in Leipzig rechtskräftig.
rechtskräftig Jetzt
kann das bisherige Bergwerk zu einem Endlager
umgerüstet und schwach- bzw. mittelradioaktive
Abfälle ab ca. 2012 sicher endgelagert werden.
101
11.5.2 Salzstock Gorleben
Der Salzstock Gorleben wird seit
1979 auf seine Eignung für die
Endlagerung aller Arten fester radioaktiver Abfälle untersucht, also
auch für die Endlagerung wärmeentwickelnder Abfälle. Eine endgültige Eignungsaussage für den
Salzstock Gorleben wird erst nach
der untertägigen Erkundung mögli h sein.
lich
i
Di
Die
B
Bewertung
t
aller
ll
bisherigen Erkundungsergebnisse
bestätigt seine Eignungshöffigkeit.
Dennoch hat der Bund die weitere
Erkundung seit Ende 2000 zur
Klärung
standortunabhängiger
Endlagerfragen unterbrochen.
www.kernenergie.de
11.5.3 Salzbergwerk Asse
Im stillgelegten ehemaligen
Salzbergwerk Asse bei Wolfenbüttel wurden Verfahren und
Techniken zur Endlagerung radioaktiver Abfälle entwickelt und
erprobt
p
und bis 1978 schwachund mittelaktive Abfälle eingelagert. Die Schachtanlage Asse
soll 2013 vollständig und sicher
verschlossen sein.
www.kernenergie.de
102
11.5.4 Morsleben (ERAM)
Das Endlager für radioaktive Ab
Abfälle Morsleben (ERAM) war bis
1998 das einzige in Betrieb befindliche Endlager für schwachund mittelradioaktive Abfälle in
Deutschland. Danach wurde die
Einlagerung eingestellt. Bis 1998
waren 36.752 m3 radioaktive Abfälle eingelagert worden. Nach Entscheidung der Bundesregierung
wird die Endlagerung nicht wieder
aufgenommen. Derzeit wird die
Stilllegung des Endlagers vorbereitet, ein entsprechendes Planfeststellungsverfahren ist eingeleitet.
www.kernenergie.de
11.6 Wiederaufbereitung
Anwendung chemischer Verfahren, um aus dem Kernbrennstoff nach seiner
Nutzung im Reaktor (abgebrannter Kernbrennstoff) die Wertstoffe - das noch
vorhandene Uran und den neu entstandenen Spaltstoff Plutonium - von den
Spaltprodukten, den radioaktiven Abfällen, zu trennen. Großtechnisch
mehrjährig erprobt ist zur Wiederaufarbeitung das PUREX-Verfahren. Ein
abgebranntes Brennelement hat - wenn man vom Strukturmaterial absieht folgende Zusammensetzung: ca. 96% Uran, 3% Spaltprodukte (Abfall), 1%
Plutonium und geringe Anteile von Transuran-Elementen. Das
zurückgewonnene Uran und das Plutonium können nach entsprechender
chemischer Bearbeitung wieder als Brennstoff in einem Kernkraftwerk
eingeset t werden.
eingesetzt
erden Die in einer Wiedera
Wiederaufarbeitungsanlage
farbeit ngsanlage mit einem
Jahresdurchsatz von 350 t jährlich zurückgewinnbaren Kernbrennstoffe
entsprechen bei Einsatz in den heute üblichen Leichtwasserreaktoren der
Energiemenge von ca. 10 Mio. t Steinkohle. Durch den
Wiederaufarbeitungsprozeß wird der hochaktive Abfall (Spaltprodukte)
abgetrennt und durch Verglasung in eine Form gebracht, die eine sichere
Endlagerung gewährleistet.
www.kernenergie.de
103
12.1 Atomphysiker
Hans Bethe
Niels Bohr
John Chadwick
Marie Curie
Pierre Curie
Paul Dirac
Albert Einstein
Otto Hahn
Liese Meitner
Max Planck
Robert Oppenheimer
Ernest Rutherford
Snyder
Arnold Sommerfeld
Fritz Straßner
Carl Friedrich von Weizäcker
12.2 Historisches...
...manchmal musste ich einen ganzen Tag lang
eine siedende Masse mit einer Eisenstange
umrühren, die fast ebenso groß war wie ich.
Abends war ich zum umfallen müde...In das
Laboratorium kamen nur sehr wenige Leute:
der eine oder der andere Physiker oder
Chemiker besuchte uns von Zeit zu Zeit,
entweder um unsere Experimente zu sehen,
oder um Pierre Curie...um
Curie um einen Rat zu bitten.
bitten
Dann gab es vor der schwarzen Tafel jene
Gespräche, an die man so gerne zurückdenkt,
weil sie auf das wissenschaftliche Interesse
und die Arbeitsintensität stimulierend wirken...
Marie Curie um 1900
104
Übungsfragen 1
11.
2.
3.
4.
5.
6.
7.
8
8.
9.
10.
11.
12.
Wie kann man Energie definieren ?
Was ist die physikalische Einheit der Energie ?
Welches Grundprinzip ist bei allen Energieumwandlungen zu berücksichtigen ?
Was versteht man unter einem Raumwinkel (EEB1) ?
Was versteht man unter einem Mol ?
Was ist ein u ?
Was ist das SI-System ?
Wie kann man Materie definieren ?
Welche Erkenntnis gewann man aus d. Experiment von RUTHERFORD ? (EEB1,SSB1)
Beschreiben Sie das BOHRsche Atommodell, wo sind die Schwächen ? (EEB1)
Wie viele Elektronen können sich maximal in der L-Schale aufhalten ?
Erläutern Sie den Welle-Teilchen Dualismus ! (EEB1,SSB1)
Übungsfragen 2
13.
13
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
Was versteht man unter der HEISENBERGschen Unschärferelation ? (EEB 1)
Was ist eine „stehende Welle“ ? (EEB1)
Was versteht man unter einem Orbital ?
Was versteht man unter Quantenzahlen, welche kennen Sie und welche Bedeutung haben
diese ? (EEB1,SSB1)
Nach welchen Prinzipien werden die Elektronenschalen besetzt (Erläuterungen) ?
Was sind die Elektronenkonfigurationen von Silizium, Zinn und Blei ?
Was sind Nukleonen, welche gibt es ?
Woraus bestehen Protonen ?
Was sind Quarks ?
Zu welchen Elementarteilchengruppen gehören Elektronen, Protonen bzw. Neutronen ?
Welche Spektrallinien (Serien) kennt man beim Wasserstoff ? (EEB1,SSB1)
Unterscheiden sich die H-Isotope in den Spektralserien ? (EEB1,SSB1)
105
Übungsfragen 3
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
Was versteht man unter der Ordnungszahl
g
eines Atoms ?
Was versteht man unter der Massezahl eines Atoms ?
Wodurch unterscheiden sich Haupt- und Nebengruppen im PS ? (SSB1)
Was sind Salzbildner ? (SSB1)
Welche Elemente sind Erzbildner ? (SSB1)
In welcher Gruppe befinden sich Uran und Plutonium ? (SSB1)
Was ist das chemische Kurzzeichen für Eisen ?
g
g ? ((EEB1,SSB1)
,
)
Was versteht man unter Ionisierungsenergie
Was versteht man unter Elektronenaffinität ? (EEB1,SSB1)
Was versteht man unter Elektronegativität ? (EEB1,SSB1)
Welches Element hat die größte Elektronegativität ? (EEB1,SSB1)
Wie viele Nuklide sind bekannt ? Wie viele davon sind stabil ?
Übungsfragen 4
37.
38.
39.
40.
41.
42.
43.
44.
45
45.
46.
47.
48.
49.
50.
Wo in der Nuklidkarte findet man die stabilen Nuklide ?
Nennen Sie die drei Isotope des Wasserstoffs ?
Besitzen die Isotope des Wasserstoff unterschiedliche physikalische Eigenschaften? Warum ?
Besitzen die Isotope des Kohlenstoff unterschiedliche chemische Eigenschaften ? Warum ?
Wie ist das Anti-Photon beschaffen (EEB1,SSB1)
Wie ist das Anti-Wasserstoff-Atom aufgebaut ? (EEB1,SSB1)
Was versteht man unter isomeren Nukliden ? (EEB1,SSB1)
Was versteht man unter Radioaktivität, was ist in diesem Zusammenhang Aktivität ?
Welche physikalische Einheit hat die Aktivität ?
Was versteht man unter einer nuklearen Kettenreaktion ?
Was ist Alpha-Strahlung ?
Woher kommen die Elektronen bei Beta-Strahlung ?
Was ist die physikalische Dimension für den radioaktiven Zerfall ?
Was für Strahlendosen kennen Sie?
106
Übungsfragen 5
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
Wie ist die Einheit für die Äquivalentdosis
q
definiert ?
Wie ist die Einheit für die Energiedosis definiert ?
In welchen Einheiten kann man Strahlungsenergie angeben ?
Was versteht man unter Dosisleistung
Wie groß ist die Dosisleistung in 2 m Abstand eines punktförmigen Cs-137 Strahlers, der
eine Aktivität von 20 000 Ci aufweist ?
Was ist die mittle Jahresdosis in Deutschland ?
Wie hoch ist die tödliche Dosis ?
Wie groß ist die Aktivität eines Standardmenschen ? (EEB1,SSB1)
Was versteht man unter dem Massendefekt ?
Welche 4 fundamentalen Kräfte kennen Sie (Erläuterungen) ?
Was ist Kernfusion, bei welchen Nukliden kann man damit Energie gewinnen ?
Was ist Kernspaltung, bei welchen Nukliden kann man damit Energie gewinnen ?
Was sagt die „Kamelhöckerkurve“ aus ?
Literatur
1
1.
Chemie für Ingenieure - von Hoinkis
Hoinkis, Jan; Lindner
Lindner, Eberhard; 2007 Wiley
WileyVCH - ISBN 3-527-31798-8
2.
Hering - Martin - Stohrer ; Physik für Ingenieure; Springer Verlag Berlin
2002, ISBN 3-540-429-64-6
3.
Dobrinski - Krakau – Vogel; Physik für Ingenieure
4.
Haliday – Resnick - Walker; Physik; Viley VCH 2001, ISBN 3-527-40366-3
5.
Schülerduden Physik, Duden Verlag Mannheim, 2004, ISBN 3-411-05375-5
6.
De Pree; Physics made simple; Broadway Books; 2004, ISBN 0-7679-17014
7.
Browne; Physics for Engineering and Science; McGraw Hill, 1998, ISBN 007-008498-X B. Bröcker; DTV-Atlas zur Atomphysik; DTV-Verlag, 1993
8.
S. Hawking; CD: Eine kurze Geschichte der Zeit; Navigo, 1997 B. Bröcker;
DTV-Atlas zur Atomphysik; DTV Verlag 1993
9.
Volkmer – Kernenergie Basiswissen; Volkmer – Radiaoaktivität und
Strahlenschutz
10. Koelzer, Lexikon der Kernenergie
107
Web-Links
http://www.kernenergie.de
http://www.kernenergie.de/r2/de/Gut_zu_wissen/Materialien/D
ownloads/?navanchor=1010023
http://de.wikipedia.org/wiki/Erde
htt // t
http://atom.kaeri.re.kr/
k i k/
http://de.wikipedia.org/wiki/Atomphysik#Moderne_Atomphysik
http://de.wikipedia.org/wiki/Kernphysik
108