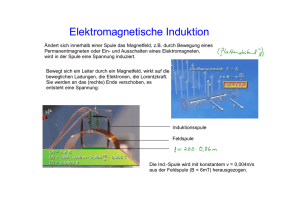
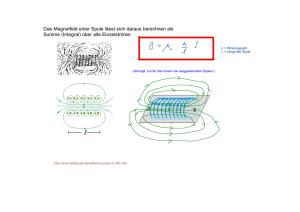
Extemporale zur Induktion 2010

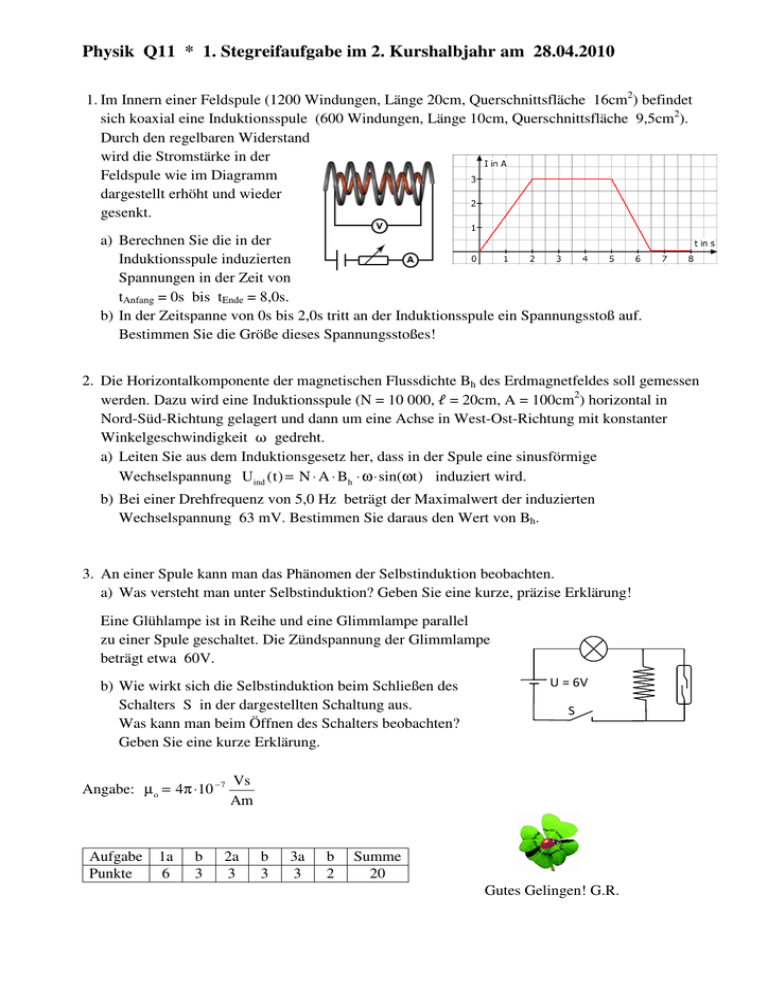
Physik Q11 * 1. Stegreifaufgabe im 2. Kurshalbjahr am 28.04.2010
1. Im Innern einer Feldspule (1200 Windungen, Länge 20cm, Querschnittsfläche 16cm2) befindet
sich koaxial eine Induktionsspule (600 Windungen, Länge 10cm, Querschnittsfläche 9,5cm2).
Durch den regelbaren Widerstand
wird die Stromstärke in der
Feldspule wie im Diagramm
dargestellt erhöht und wieder
gesenkt.
a) Berechnen Sie die in der
Induktionsspule induzierten
Spannungen in der Zeit von
tAnfang = 0s bis tEnde = 8,0s.
b) In der Zeitspanne von 0s bis 2,0s tritt an der Induktionsspule ein Spannungsstoß auf.
Bestimmen Sie die Größe dieses Spannungsstoßes!
2. Die Horizontalkomponente der magnetischen Flussdichte Bh des Erdmagnetfeldes soll gemessen
werden. Dazu wird eine Induktionsspule (N = 10 000, ℓ = 20cm, A = 100cm2) horizontal in
Nord-Süd-Richtung gelagert und dann um eine Achse in West-Ost-Richtung mit konstanter
Winkelgeschwindigkeit ω gedreht.
a) Leiten Sie aus dem Induktionsgesetz her, dass in der Spule eine sinusförmige
Wechselspannung Uind (t) = N ⋅ A ⋅ Bh ⋅ ω⋅ sin(ωt) induziert wird.
b) Bei einer Drehfrequenz von 5,0 Hz beträgt der Maximalwert der induzierten
Wechselspannung 63 mV. Bestimmen Sie daraus den Wert von Bh.
3. An einer Spule kann man das Phänomen der Selbstinduktion beobachten.
a) Was versteht man unter Selbstinduktion? Geben Sie eine kurze, präzise Erklärung!
Eine Glühlampe ist in Reihe und eine Glimmlampe parallel
zu einer Spule geschaltet. Die Zündspannung der Glimmlampe
beträgt etwa 60V.
b) Wie wirkt sich die Selbstinduktion beim Schließen des
Schalters S in der dargestellten Schaltung aus.
Was kann man beim Öffnen des Schalters beobachten?
Geben Sie eine kurze Erklärung.
Angabe: µ o = 4π ⋅10 − 7
Aufgabe
Punkte
1a
6
b
3
U = 6V
S
Vs
Am
2a
3
b
3
3a
3
b
2
Summe
20
Gutes Gelingen! G.R.
Physik Q11 * 1. Stegreifaufgabe im 2. Kurshalbjahr am 28.04.2010 * Lösung
•
1. a) Uind = − N I ⋅ A I ⋅ B = − N I ⋅ A I ⋅µ o ⋅
NF •
Vs 1200 •
⋅ I = − 600 ⋅ 0, 00095m 2 ⋅ 4π ⋅10−7
⋅
⋅I =
ℓF
Am 0, 20m
A

−3 Vs
 − 4,30 ⋅10 A ⋅ 1,5 s = − 6, 5 mV

•
0 mV

−3 Vs
= − 4,30 ⋅10
⋅I = 
A
 + 4,30 ⋅10−3 Vs ⋅ 2, 0 A = 8, 6 mV

A
s

0 mV

b) Spannungsstoß = − N I ⋅ ( Φ(2,0s) − Φ (0, 0s) ) = − N I ⋅ A I ⋅µ o ⋅
= − 600 ⋅ 0, 00095m 2 ⋅ 4π ⋅10−7
;
0, 0s < t < 2, 0s
;
2, 0s < t < 5, 0s
;
5, 0s < t < 6, 5s
;
6, 5s < t < 8, 0s
NF
⋅ 3, 0A =
ℓF
Vs 1200
⋅
⋅ 3, 0A = − 0, 013 Vs
Am 0, 20m
•
2. a) A(t) = A ⋅ cos(ωt) und A(t) = − A ⋅ sin(ωt) ⋅ ω = − A ⋅ ω⋅ sin(ωt)
•
Uind = − N ⋅ Bh ⋅ A(t) = − N ⋅ Bh ⋅ (− Aω sin(ωt)) = N ⋅ Bh ⋅ A ⋅ ω sin(ωt)
b) Uind = N ⋅ Bh ⋅ A ⋅ ω sin(ωt) ⇒ Uind,max = N ⋅ Bh ⋅ A ⋅ ω ⇒
Bh =
U ind,max
N⋅A⋅ω
=
Uind,max
N ⋅ A ⋅ 2π ⋅ f
=
0, 063V
10000 ⋅ 0, 010m 2 ⋅ 2π ⋅ 5, 0
1
s
= 2, 0 ⋅10−5 T = 20 µT
3. a) Ändert sich die elektrische Stromstärke durch eine Spule, so ändert sich der magnetische
Fluss durch die Spule und es wird daher eine Spannung in der Spule induziert, welche
nach der Regel von Lenz die Änderung der Stromstärke zu verhindern sucht.
b) Beim Einschalten:
Beim Ausschalten:
Die Stromstärke erreicht nicht sofort ihren Maximalwert, sondern
wächst erst „langsam“ an. Glühlampe leuchtet dann, Glimmlampe
zündet nicht.
Plötzliche Abnahme der Stromstärke führt zu einer so hohen
Induktionsspannung, dass die Glimmlampe zündet.