Aufgabe 1

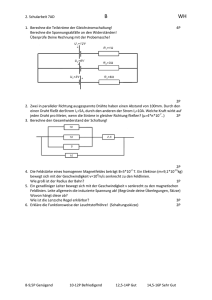
Aufgabe 1
1. Warum stehen elektrische Feldlinien im statischen Fall immer senkrecht auf Oberflächen
von Leitern?
kN
wird ein geladenes Teilchen
C
( q  25nC ) unter einem Winkel von 30 zu den Feldlinien 1,2cm weit gegen das Feld
transportiert. Berechne die dafür erforderliche Energie.
2. In einem homogenen Feld der Feldstärke E  85
3. Ein Öltröpfchen ( m  3,5 pg ) schwebt im homogenen Feld zwischen zwei Platten mit dem
Abstand d  5mm bei einer Spannung U  214V .
Wie viel Elementarladung trägt es?
Aufgabe 2
Zwei Punktladungen Q1  2C und Q2  8C haben den Abstand d  1m .
In welchem Punkt ist die Feldstärke null?
Aufgabe 3
Auf einem Plattenkondensator wird bei einer Spannung U  200V ohne Glasfüllung
Q0  20nC und mit Glasfüllung Q1  110nC gemessen.
Bestimme  r für Glas.
Lösung 1
1. Würden die elektrischen Feldlinien nicht senkrecht auf der Leiteroberfläche stehen, so
gäbe es eine Komponente des elektrischen Feldes parallel zur Leiteroberfläche, die zu einer
Verschiebung von Ladungen führen würde. Der stationäre Zustand wäre also noch nicht
erreicht.
2 . E  W  q  E  q  E  d  cos 30  2,2  10 5 Nm  22J
3. m  g  q 
U
d
 q  8,0  10 19 C  5e
Lösung 2
Aus E  E1  E 2 
1  Q1 Q2 
 
  0 und r1  r2  1m folgt
4 0  r12 r22 
1
2
r1  m und r1  m
3
3
Lösung 3
Aus
Q0
Q
A
A
  0  und 1   0  r  folgt
U
d
U
d
r 
Q1
 5,5
Q0
Aufgabe 4
Wie groß müsste die Plattenfläche eines luftgefüllten Plattenkondensators sein, der bei
einem Plattenabstand von d  1mm und einer Spannung von U  220V die gleiche Energie
speichert wie eine Autobatterie von 12V und 88Ah?
Aufgabe 5
1. Aus vier Widerständen R1  10 , R2  20 ,
R3  50 und R4  100 werden die abgebildeten
Schaltungen aufgebaut. An jede Schaltung wird eine
Spannung von 24V angelegt. Berechne
a) den Gesamtwiderstand und
b) die an jedem Widerstand anliegende Spannung
2. Berechne die die größte und kleinste Gesamtkapazität aus C1  1F , C2  1F ,
C3  2F und C4  4F
Aufgabe 6
Kupfer hat die gemittelte Atommasse mCu  63,546u .
Wie lange muss ein Strom der Stärke I  0,45 A fließen, damit aus einer CuCl2-Lösung
3,5 g Kupfer abgeschieden wird?
Lösung 4
Ladung der Batterie 88 Ah  316800 As .
Energie der Batterie E  Q  U  3,8MJ
1
1
A
Energie des Plattenkondensators: E  CU 2   0   U 2
2
2
d
4
2
Es ergibt sich: A  1,8  10 km
Lösung 5
1. a) A: 180 , B: 25 , C: 5,56 , D: 22,5 , E: 40 , F: 124,29
b) A: U1  1,33V , U 2  2,67V , U 3  6,67V , U 4  13,33V
B: U1  U 3  8V , U 2  U 4  16V
C: U1  U 2  U 3  U 4  24V
D: U1  10,67V , U 2  U 3  U 4  13,33V
E: U1  U 2  4V , U 3  U 4  20V
F: U1  1,93V , U 2  U 3  2,76V , U 4  19,31V
2. Bei Parallelschaltung Cmax  8F , bei Reihenschaltung Cmin  0,36F
Lösung 6
1mol Kupfer ( 6,02  10 23 Kupferatome) haben die gemittelte Masse m  63,546 g . In
3,5 g Kupfer sind somit 3,32  10 22 Kupferatome enthalten.
In der CuCl2-Lösung ist Kupfer zweiwertig, d.h. es werden pro Kupferatom 2 Elektronen
(2e  3,20  10 19 C ) für die Neutralisation und Abscheidung benötigt.
Insgesamt wird die Ladung q  3,32  10 22  (3,20  10 19 C )  1,06  10 4 C benötigt.
q
Aus I  0,45 A  folgt t  2,36  10 4 s  6,6h
t