Computergestützte Mechanik

Technische Universität Chemnitz
Institut für Physik
Prof. Dr. A. Thränhardt
Wintersemester 2009/10
Di, 17.11.2009
Computergestützte Mechanik
2. Projekt
Abgabe: Montag, 14.12.2009
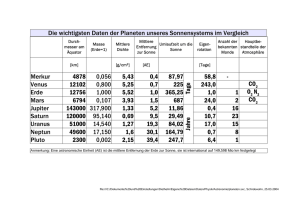
Numerische Berechnung der Bewegung der Planeten im Sonnensystem
Betrachten Sie die Bewegung der vier inneren Planeten unseres Sonnensystems.
Folgende Daten für die vier inneren Planeten seien bekannt:
Masse
[1024 kg]
Sonne 1989100
Merkur 0.3022
Venus
4.8685
Erde
5.9737
Mars
0.6418
Radius Große Halbachse a
numerische
6
[10 m]
[AE]
Exzentrizität ε
696
2.439764
0.387099
0.205631
6.051590
0.723332
0.006773
6.378150
1
0.016710
3.397000
1.523662
0.093412
Astronomische Einheit: 1 AE = 149.597870 · 109 m
Gravitationskonstante: G = 6.67259 · 1011 m3 /(kg · s2 )
Länge des
aufst. Knotens Ω [◦ ]
48.448
76.769
49.634
Aufgabe 1
a) Berechnen Sie die mittlere Umlaufzeit T für jeden Planeten bezüglich der Sonne
(Hinweis TErde = 365.24 Tage)
b) Berechnen Sie die Anfangsbedingungen {~ri (t0 ), ~r˙i (t0 )} für alle Planeten, dabei sollen alle Planeten zum Zeitpunkt t0 = 0 entweder in ihrem jeweiligen Aphel oder
Perihel stehen. Nutzen Sie hierzu zum Beispiel die Beziehung:
q
a+e
Geschwindigkeit im Perihel: vp = ϑ̇p (a − e) = 2π
a
T
q a−e
a a−e
Geschwindigkeit im Aphel: va = ϑ̇a (a − e) = 2π
T
a+e
(Hinweis vaErde = 2.57352 · 109 m/Tag)
c) Finden Sie eine sinnvolle Normierung für Längen-, Zeit- und Gewichtseinheiten
(Nl , Nt , Nm ), um in der Simulation nicht in den Bereich der numerischen Grenzen
Nl3
zu geraten (z.B.: 1 = G · Nm ·N
2 ).
t
Aufgabe 2
a) Simulieren Sie die Bewegung der vier inneren Planeten im Sonnensystem, diese
aber unabhängig voneinander. Das heißt, die Sonne wird als ortsfest betrachtet,
die Wechselwirkung findet nur zwischen der Sonne und dem jeweiligen Planeten
statt. Messen Sie die Umlaufzeit der Planeten für verschiedene Zeitschrittweiten
und vergleichen Sie diese mit den in 1.a) berechneten.
b) Betrachten Sie nur die Bahn der Erde. Setzen Sie die Masse der Erde und der
Sonne gleich, ohne die restlichen Anfangsbedingungen zu ändern. Was passiert
mit der Bahnkurve und der Umlaufzeit?
c) Simulieren Sie die Bewegung der 4 inneren Planeten und der Sonne im Sonnensystem als ein System von Massepunkten. Das heißt, alle Wechselwirkungen zwischen
den Planeten müssen berücksichtigt werden. Vergleichen Sie die Planetenbahnen,
den Ort der Sonne und die Umlaufzeiten mit denen aus a) für verschiedene Zeitschrittweiten.
d) Erhöhen Sie schrittweise (in 10er Potenzen) die Masse der Erde. Wie lang bleibt
unser Sonnensystem stabil?