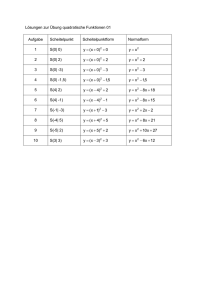
Aufgabe 1 25

1. Klausur Mathematik
EF
2.10.2013
Lösung / Bewertung
Aufgabe 1
a)
3
b)
3
c)
3
d)
3
e)
2
3
f)
3
g)
5
25
Gegeben sind die Punkte A( - 2 | - 2 ) B( 8 | 0 ) und C( 7 | 5 ).
Seite 3
1. Klausur Mathematik
EF
2.10.2013
Seite 4
Lösung / Bewertung
Die bewerteten Anteile sind im Folgenden jeweils durch Unterstrich markiert
Aufgabe 2
a)
b)
c)
3
4
4
20
Kosten bei 2 ⋅ 24 = 48 Abzügen ; zwei CD's mit je 24 Bildern und einem Abzug pro Bild:
Foto Fix:
2,80 € + 0,25 € ⋅ 24 ⋅ 2 = 14,80 € ;
Gut & günstig:
0,35 € ⋅ 48 = 16,80 €
Bilderwelt:
3,70 € + 0,15 ⋅ 24 ⋅ 2 € = 10,90 €
Zuordnungsgleichungen Anzahl x der Abzüge → Kosten y einer CD für
Foto Fix:
y = 2,80 + 0,25 x
Gut & günstig:
y = 0,35 x
Bilderwelt:
y = 3,70 + 0,15 x
S1
Schnittpunkte der Geraden
Foto Fix ∩ Gut & günstig:
S2
S3
2,80 + 0,25 x = 0,35x ó x = 28
Einsetzen z. B. bei Gut & günstig:
0,35 ⋅ 28 = 9,80 ⇒
3
S1 ( 28 | 9,80 )
Foto Fix ∩ Bilderwelt:
2,80 + 0,25 x = 3,70 + 0,15 x
Einsetzen z. B. bei Foto Fix:
2,80 + 0,25 ⋅ 9 = 5.05
3
x=9
S2( 9 | 15,05 )
Gut & günstig ∩ Bilderwelt:
0,35 x = 3,70 + 0,15 x
ó
Einsetzen z. B. bei Gut & günstig:
Erläuterung:
1
1
1
x = 18,5
0,35 ⋅ 18,5 = 6,475
S3( 18,5 | 6,475 )
Bei einem Schnittpunkt von zwei Graphen sind die Kosten der beiden Anbieter gleich,
wenn die Anzahl der Abzüge dem x -Wert entspricht.
Bis zu einer Anzahl von 18 Abzügen ist Gut & günstig der preiswerteste Anbieter,
ab einer Anzahl von 19 Abzügen ist Bilderwelt der preiswerteste Anbieter .
1. Klausur Mathematik
EF
2.10.2013
Seite 5
Lösung / Bewertung
Aufgabe 3
18
Ein Güterzug fährt um 12:00 Uhr durch
den Bahnhof von Köln. Ein Regionalexpress folgt später. Er ist schneller als der
Güterzug. Im Diagramm wurde dargestellt,
wann sich die Züge wie weit von Köln
entfernt haben.
a)
Da der Regionalexpress Köln später passiert und schneller ist (Graph steiler), wird er durch den
steileren roten bzw. zum Schluss oberen Graphen beschrieben und hält etwa 2 h nach seiner
6
Durchfahrt durch Köln auf der Strecke an.
Für 2,5 h < t < 2,6 h sind die Funktionswerte gleich (die Strecke ist etwa ----- s = 260 km ).
b)
3
Aus dem Graphen (grün markiert): Nach zwei Stunden hat der Güterzug ca. 160 km zurückgelegt.
c)
3
Die Ausweichstelle (Überhol- / Schnitt stelle der Graphen) ist etwa 110 km von Köln entfernt.
d)
3
Zeit für erste 100 km aus dem Graphen:
Regionalexpress: 1,3 h - 0,5 h = 0,8 h = 48 min Der Güterzug benötigt etwa 1,25 h = 75 min
e)
3
Die Durchschnitssgeschwindigkeit des Güterzuges ist v( s = 200km) =
s 200km
km
=
= 80
t
2,5h
h
Aufgabe 4
Die Seitenzahlen beziehen sich auf unser Lehrbuch
10
Entscheide mit Begründung, welche der folgenden Funktionen quadratische Funktionen sind:
Kurz: Eine (Potenz- ) Funktion ist quadratisch (oder vom Grad 2) , wenn die Variable quadratisch (die höchste auftretende Potenz der Variablen ist 2) und sonst allenfalls lineare oder
absolute Summanden auftreten. Speziell hier...
(1)
2
Die Funktion ist eine quadratische Funktion, da sich der Funktionsterm durch einfaches Umstellen auf die Normalform (oder allgemeine Form) einer quadratischen Funktion (s.S. 23) umstellen lässt.
Die Normalform einer quadratischen Funktion hat die Form:
, wobei a
sind. Da
gilt hier a = - 0,9
0 gelten muss und b und c beliebige reelle Zahlen
0, b = 0,15 und c = 4
1. Klausur Mathematik
EF
2.10.2013
Seite 6
Lösung / Bewertung
(2)
2
Auch diese Funktion ist eine quadratische Funktion; sie ist in der Scheitelpunktform
gegeben. Die Scheitelpunktform (s.S. 23) hat die Form:
, mit
a 0 und
und
beliebige reelle Zahlen.
Bei der gegebenen Funktion ist a = 1 ≠ 0, und
= - 4 und
= - 0,1.
Alternativ kann man auch die Scheitelpunktform in die Normalform umformen (Klammer mit der binomischen Formel auflösen!) und dann ergibt sich
(3)
2
Diese Funktionsgleichung lässt sich umstellen zu f(x) = 19,1x – 4, woran man leicht
erkennt, dass es eine lineare und keine quadratische Funktion ist. Die Normalform einer quadratischen Funktion ist nicht gegeben; der Funktionsterm ließe sich zwar auf
die Form
bringen, aber dann wäre a = 0, was bei quadratischen Funktionen ausgeschlossen ist.
(4)
2
Diese Funktionsgleichung gehört zu einer quadratischen Funktion; sie ist in der faktorisierten Form gegeben (s.S. 23). Die faktorisierte Form einer quadratischen Funktion
ist mit a ≠ 0 und x1 und x2 beliebige reelle Zahlen. Im
gegebenen Fall ist a = 1, x1 = - 2 und x2 = 0.
Alternativ kann man die Klammern auflösen und erhält wieder die Normalform einer
quadratischen Funktion
(5)
2
mit a =1, b = 2 und c = 0.
Die gegebene Funktionsgleichung gehört nicht zu einer quadratischen Funktion, da sie
sich durch Termumformungen nicht auf die Normalform einer quadratischen Funktion
bringen lässt, da es einen Summand x3 gibt.
Hinweise: 3x3 + 0,1x2 kann man nicht zusammenfassen, schon gar nicht zu 3,1x5 !
Was sollte ein Meter und ein Quadratmeter auch geben; ein "Pentro"-meter ?
Aufgabe 5 23
a) Bestimme die Nullstellen folgender Funktionen:
Allgemein: Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist; also
(1) 3
f ( x) = ( x + 3,5)(x −1,5) = 0
x+ 3,5 = 0 | -3,5
x = -3,5
(2)
3
oder
oder
x - 1,5 = 0
| +1,5
x = 1,5
f (x) = x2 − 7x = x⋅ (x-7) = 0 , also x = 0 oder x = 7 sind die gesuchten Nullstellen
1. Klausur Mathematik
EF
2.10.2013
Seite 7
Lösung / Bewertung
(3)
2
f ( x) = 4 x + 0,8 = 0 | - 0,8
4x = -0,8
|:4
x = -0,2 ist die gesuchte Nullstelle
(4)
3
f (x) = (x − 6)2 + 3 = x² - 12x + 39 = 0 x 1;2 = 6 ± 36 − 39 = 6 ± - 3
hat keine Lösung / Nullstellen, denn der Ausdruck unter der Wurzel ist negativ
oder kurz : (x - 6)² = - 3 ist unlösbar, da Quadrat nie negativ wird.
(5)
3
f (x) = 0,19x2 + 0,1 = 0 <=>
0,19 x² = - 0,1 | : 0,19 <=> x² < 0
Quadratzahlen sind aber immer positiv, also gibt es keine Lösung / Nullstellen.
(6)
4
f ( x) = x 2 + 2 x − 1 = 0 mit "pq-Formel"
x 1;2 = 1 ± 1 + 1 = 6 ± 2
also
b)
5
x = 0,414 oder x = - 2,414
Bestimme für die erste Funktion
⇔
⇔
sind die gesuchten Nullstellen.
f ( x) = ( x + 3,5)(x −1,5)
die Koordinaten des Scheitelpunktes S.
Der x-Wert des Scheitelpunkts liegt „in der Mitte“ zwischen den Nullstellen; d.h.
auf der halben Strecke zwischen den Nullstellen.
Die Nullstellen der Funktion sind x1 = -3,5 und x2 =1,5 (siehe 5 a) (1) ,
also die Mitte ist die Stelle xS = [-3,5 + 1,5] : 2 = - 2 : 2 = - 1 .
Dann
xS = - 1 einsetzen in f(x)
also f(-1) = (- 1 + 3,5)(-1 - 1,5) = 2,5⋅ (- 2,5) = - 6,25
Der Scheitelpunkt ist also S( -1 | - 6,25 )