MedAT Teil I-1: Mathematik – Zehnerpotenzen

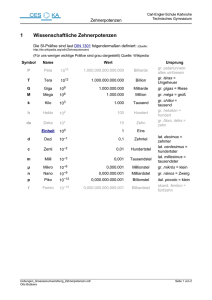
MedAT H & Z
Vorbereitungskurs
für den Aufnahmetest an den
österreichischen medizinischen Universitäten
am 8.Juli 2016
Teil I - 1
Mathematik - Zehnerpotenzen
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Zehnerpotenzen
Zeherpotenzen sind die (ganzzahligen) Potenzen von der Zahl Zehn.
Zum Beispiel:
101 = 10
102 = 100
103 = 1000
usw.
Die Hochzahl (Potenz) gibt die Anzahl an Nullen an.
:
Das Komma nach rechts verschoben.
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Zehnerpotenzen
Außerdem gilt:
100 = 1
10 -1 = 0,1
10-2= 0,01
usw.
Die Hochzahl kann auch negativ sein.
Das Komma wird dann entsprechend nach links
verschoben.
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Präfix
Ein Präfix ist eine Worterweiterung (Affix), die dem Wortstamm vorangestellt
wird (im Gegensatz zum Suffix, das dem Stamm folgt). (Wikipedia)
●
●
●
Präfixe sind Vorsilben.
In der Mathematik werden sie als Vorsilbe für Zehnerpotenzen
verwendet.
Ein sehr bekanntes Präfix ist kilo. Es bedeutet einfach
„tausend“. Man sagt Kilogramm oder Kilometer anstatt
„tausend Gramm“ oder „tausend Meter“.
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Die wichtigsten Präfixe (Teil 1)
Name
Präfix
Abkürzung
Zahl in
Dezimalschreibweise
Zahl in
Exponentialschreibweise
Zehn
Deka
de
10
101
Hundert
Hekto
ha
100
102
Tausend
Kilo
K oder k
1.000
103
Million
Mega
M
1.000.000
106
Milliarde
Giga
G
1.000.000.000
109
Billion
Tera
T
1.000.000.000.000
1012
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Die wichtigsten Präfixe (Teil 2)
Name
Präfix
Abkürzung
Zahl in
Dezimalschreibweise
Zahl in
Exponentialschreibweise
Zehntel
Dezi
d
0,1
10-1
Hundertstel
Centi
c
0,01
10-2
Tausendstel
Milli
m
0,001
10-3
Millionstel
Mikro
µ
000 000,1
10-6
Milliardstel
Nano
n
000 000 000,1
10-9
Billionstel
Pico
p
000 000 000 000,1
10-12
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1. Zehnerpotenzen und Präfixe
●
Wissenschaftliche Schreibweise
Wenn man mit sehr großen oder sehr kleinen Zahlen hantiert, so
schreibt man diese normalerweise so an dass nur eine Ziffer links
vom Komma steht!
●
Beispiel: Man sagt/schreibt:
In 18g Wasser befinden sich ca. 6,022 ⋅ 1023 Wassermoleküle *.
Man könnte stattdessen z.B. auch 60,22 ⋅ 1022 schreiben. Das wäre
nicht falsch, aber unüblich.
(*Avogadro-Konstante, eine unvorstellbar große Zahl. Aber man muss sie sich nicht
vorstellen können um mit ihr zu rechnen ;)
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1.1 Rechnen mit Zehnerpotenzen
●
●
Multiplizieren und Dividieren
Beim Multiplizieren von Zahlen mit Zehnerpotenzen werden die
Hochzahlen addiert.
Bsp.:
●
105 ⋅ 103 = 105 + 3 = 108
Beim Dividieren von Zahlen mit Zehnerpotenzen werden die
Hochzahlen subtrahiert.
Bsp.:
105 : 103 = 105 – 3 = 102
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1.1 Rechnen mit Zehnerpotenzen
●
●
●
Multiplizieren und Dividieren
Auch bei negativen Hochzahlen gelten einfach die Gesetzte der
Addition:
Bsp.:
105 ⋅ 10 – 3 = 105 + ( – 3) = 102
Bsp.:
10 – 5 : 103 = 10 (– 5) – 3 = 10 – 8
Wenn „normale“ Zahlen auch dabei sind ist es am besten man
rechnet beide Arten von Zahlen getrennt voneinander:
Bsp.:
2 ⋅ 10 – 6 ⋅ 7 ⋅ 102 = 14 ⋅ 10 – 6 + 2 =
14 ⋅ 10 – 4 oder 1,4 ⋅10 – 3
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1.2 Übungsbeispiele
Schreibe in wissenschaftlicher Schreibweise an:
0,07762
0,007762 ⋅ 10-3
792634,78
792634,7 ⋅ 10-5
523,62
523,62 ⋅ 103
700000
0,647 ⋅ 10-7
723,827364
60723,827364 ⋅ 10-9
23,72631
23,072631 ⋅ 107
237,0007
0,00237,0007 ⋅ 10-4
76239,237
76239,237 ⋅ 102
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at
1.2 Übungsbeispiele
●
●
●
●
Wenn sich in 18g Wasser 6,022 ⋅ 1023 Wassermoleküle befinden, wie
viele sind dann in 36g (der doppelten Menge) vorhanden?
Die Erde hat eine Masse von ca. 5,9722 ⋅ 1024 kg. Der Mond hat ca.
7,348 ⋅ 1022 kg. Um wie viel mal mehr Masse hat die Erde gegenüber
dem Mond?
Erythrozyten (Rote Blutkörperchen) haben einen Durchmesser von
ca. 7,5 µm. Es befinden sich ca. 30 Billionen in einem menschlichen
Körper. Welche Länge ergäbe es wenn alle Erythrozyten aneinander
gereiht werden würden?
Der Abstand zum Mond beträgt ca. 384.400 km. Wie weit ist das im
Vergleich zur Länge der Erythrozyten-Reihe aus obigen Beispiel?
lernvorsprung.at
...der Wissensvorsprung für Dein Studium!
© 2016 lernvorsprung.at